آموزش بهینه سازی ازدحام ذرات یا PSO — مرور مفاهیم و دستورات
الگوریتم بهینه سازی ازدحام ذرات یا Particle Swarm Optimizatoion (به اختصار PSO) یکی از مهم ترین الگوریتم های بهینه سازی هوشمند است که در حوزه هوش ازدحامی (Swarm Intelligence) جای می گیرد.

جلسه اول: مبانی تئوری بهینه سازی ازدحام ذرات PSO (Particle Swarm Optimization)
این الگوریتم:
- از جمله روش های metaheuristic (فرابتکاری) است.
- علی رغم سادگی قدرت بالایی را داراست.
- ذاتا الگوریتمی پیوسته است و لذا برای مسائل بهینه سازی در حوزه پیوسته بیشتر کاربرد دارد.
- البته با تمهیداتی می توان آن را برای مسائل گسسته نیز به کار برد.
- در شاخه swarm intelligence یا هوش جمعی (ازدحامی) قرار می گیرد.
- گاها به عنوان الگوریتم تکاملی (evolutionary) طبقه بندی می شود. چون مکانیزم بهبودیابنده در حال تکرار است.
- الگوی جدیدی را که اصل و اساس آن بر مبنای به اشتراک گذاری اطلاعات است معرفی می کند.
نکته: الگوریتم های فراابتکاری الگوریتم هایی هستند که با کمترین اطلاعات مسأله را حل می کنند.
نکته: ضعف عمده الگوریتم ژنتیک این است که مفهوم همکاری یا جریان اطلاعاتی در آن وجود ندارد.
در حالی که در هوش ازدحامی(جمعی)، information flow یا جریان اطلاعاتی یکی از پیش نیازهای اصلی است که منجر به وجود همکاری می گردد. نکته بعدی این است که وقتی می خواهیم همکاری هدفمندی در یک جمع ایجاد کنیم، نیازمند مفهومی به نام خودترتیبی یا self-organization هستیم و باید اسلوب و قاعده ای جمعیت را کنترل کند.
• در بحث هوش ازدحامی سعی می کنیم مفهوم خودترتیبی را با استفاده از یک سری قوانین ساده که همه ملزم به رعایت آن هستند، ایجاد کنیم.
• هرجا جریان اطلاعاتی و خودترتیبی وجود داشته باشد، هوش جمعی به وجود خواهد آمد.
مثال:
۱) مغز انسان ذاتا هوشی جمعی از نورون ها است.
۲) کلونی مورچه ها، زنبورها و موریانه ها
۳) الگوریتم رقابت استعماری
۴) عملکرد پرندگان و ماهی ها
به عنوان مثال عملکرد ماهی ها و چند دسته شدن آنان هنگام مواجهه با خطر شکارچی و سپس متحد شدن دوباره آنان بعد از دفع خطر، باعث شده که الگوریتم Artificial Fish Swarm الهام گرفته شود. در این رابطه باید موارد زیر را در نظر گرفت:
- تبادل اطلاعات: هر ماهی با اطرافیان در ارتباط است.
- خودترتیبی: تعداد محدودی قانون وجود دارد، به عنوان مثال هر ماهی در جهتی حرکت می کند که اطرافیان حرکت کنند.
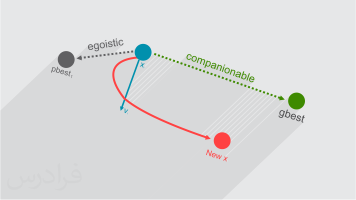
PSO: ذراتی را در نظر بگیرید که هریک موقعیتی (یکی از راه حل های ممکن مسأله بهینه سازی) در فضای جستجو دارند و در این فضا در حرکت اند. قانون حرکتی این ذرات برای همه ثابت است و همگی در حرکت خود از تجارب قبلی خود و تجارب قبلی جمع بهره می برند تا زمانی که معیارهای مشخص شده به کمینه مقدار یا بیشینه مقدار خود برسند.
هر ذره دارای پنج خاصیت است:
موقعیت Xt
مقدار تابع هدف متناظر با موقعیت X i,cost
سرعت V t
بهترین موقعیت تجربه شده توسط ذره تاکنون X i,best
مقدار تابع هدف متناظر با بهترین موقعیت تجربه شده توسط ذره تاکنون X i,best cost
نکته: سرعت، جهت حرکت را نشان می دهد چون می دانیم بردار سرعت مماس بر جهت حرکت است در واقع سرعت، جهت حرکتی است که باید پیموده شود تا از موقعیت پیشین به موقعیت کنونی برسد.
نکته: تابع هدف (objective function) در صورت کمینه یابی تابع هزینه (cost function) یا تابع خطا (error function) نامیده می شود.
نکته: تابع هدف (objective function) در صورت بیشینه یابی تابع برازندگی (fitness function) یا تابع سود (profit function) نامیده می شود.
قوانین self-organization (خودترتیبی) در PSO
در هر iteration (تکرار)، ذره باید:
۱) مقداری در جهت حرکت فعلی خود.
۲) مقداری به سمت بهترین خاطره خود.
۳) مقداری به سمت بهترین خاطره کل ذرات.
حرکت کند تا به موقعیت جدید برسد. بردار سرعت جدید برایند سه بردار پیشین است.
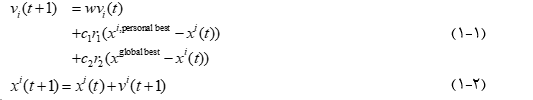
در رابطه (۱-۱)، w ضریب اینرسی نامیده می شود. چون ضریبی است که جهت حرکت کنونی Vi (t) را به جهت حرکت بعدی vi (t+1) مرتبط می گرداند. به عبارت دیگر نشانگر میزان تمایل ذره برای حفظ حالت حرکت کنونی خود است. این عدد بایستی کمتر از ۱ باشد و مقدار مناسب آن بین ۴/۰ الی ۹/۰ است. چگونگی تنظیم آن در جلسه دوم بیشتر بررسی خواهد شد.
اینرسی هرچقدر کمتر باشد الگوریتم سریع تر همگرا خواهدشد و بیشتر شدن آن باعث بالا رفتن تعداد حرکت های ناگهانی ذرات خواهد شد.
همچنین در رابطه (۱-۱)، r1 و r2 هرکدام بردارهایی به طول بردار موقعیت هستند. هر یک از اعضای این دو بردار عددی تصادفی بین ۰ و ۱ با توزیع یکنواخت است.
![]()
مقصود از rij عضو j ام بردار r1 یا r2 است. اینکه گفته می شود r1 و r2 هرکدام بردارهایی به طول بردار موقعیت هستند و روی اسکالر نبودن آنان تاکید می شود این است که در کتاب Particle Swarm Optimization نوشته Maurice Clerc صریحا بیان شده است که ضرب بردار (x(i,Personal best)-xi (t)) یا بردار (x(Global best)-xi (t)) در یک اسکالر تصادفی (تولید یک عدد رندوم برای تمامی مولفه ها) به الگوریتم PSO منجر نخواهد شد، بلکه الگوریتم دیگری را نتیجه خواهد داد. لذا جهت افزایش تنوع الگوریتم PSO نیاز به تولید یک رندوم جداگانه جهت هر مولفه می باشد.
در رابطه (۱-۱)، c1 و c2 ضرایب یادگیری نام دارند. c1 ضریب یادگیری شخصی و c2 ضریب یادگیری جمعی است. مرسوم است که c1 و c2 اعدادی نامنفی و حداکثر برابر ۲ باشند. لذا غالبا داریم:

در ارتباط با چگونگی تعیین c1 و c2 نیز در جلسه دوم بحث خواهد شد ولی به یاد داشتن مطالب شرح داده شده در ذیل حائز اهمیت است:
در الگوریتم های بهینه سازی همواره با دو مفهوم روبرو هستیم:
- جستجو (exploration) که به مفهوم توانایی تولید پاسخ های جدید و جستجوی تصادفی است.
- بهره برداری (exploitation) که به مفهوم توانایی پروراندن پاسخ های فعلی و جستجوی محلی است.
بر همین اساس افزایش w، c1 و c2 به نفع exploration و کاهش آنان به نفع exploitation است و معمولا الگوریتم های بهینه سازی به گونه ای پیاده سازی می گردند که در ابتدای کار نرخ exploration بالا و نرخ exploitation کم باشد و رفته رفته از نرخ exploration کاسته و به نرخ exploitation اضافه شود. لذا مقتضی است هنگام پیاده سازی به این مهم توجه شود و مقادیر w، c1 و c2 در ابتدای کار بالا انتخاب شده و رفته رفته کاهش یابد.
در هر iteration باید بررسی شود که آیا ذره رکورد پیشین خود را پشت سر گذاشته یا خیر و به تبع آن personal best باید آپدیت شود.
شرط شکسته شدن رکورد شخصی توسط ذره i ام جمعیت یعنی x i (در حالت مینیمم یابی):
![]()
همچنین اگر رکورد خود را پشت سر گذاشته باشد، امکان پشت سرگذاشتن رکورد جمع نیز وجود دارد لذا بایستی بررسی و در صورت نیاز رکورد جمع را آپدیت کنیم.
شرط شکسته شدن رکورد عمومی(کلی) توسط ذره i ام جمعیت یعنی x i (در حالت مینیمم یابی):
![]()
نکته: در مواقعی به جای آن که global best را منبع الهام قرار دهند، به صورت محلی (local) عمل می کنند. یعنی یک همسایگی تعریف و بهترین ذره موجود در آن (local best) را تعیین می کنند.
نکته: در مواقعی هم global best و هم local best را جهت آپدیت مورد استفاده قرار می دهند.
مراحل الگوریتم PSO:
۱) ایجاد جمعیت اولیه و ارزیابی آن
۲) تعیین بهترین خاطرات شخصی و بهترین خاطره جمعی
۳) بروزرسانی سرعت و موقعیت
۴) در صورت برآورده نشدن شرایط توقف به مرحله ۲ می رویم.
۵) پایان
شرایط توقف: چند نوع شرط توقف قابل تعیین است:
۱) رسیدن به حد قابل قبولی از پاسخ
۲) سپری شدن تعداد تکرار یا زمان مشخص
۳) سپری شدن تعداد تکرار یا زمان مشخص بدون مشاهده بهبود خاص در نتیجه
۴) بررسی تعداد مشخصی از پاسخ ها (NFE: Number of Function Evaluations)
چنانچه جمعیت اولیه را در الگوریتم PSO برابر npop در نظر بگیریم، رابطه زیر برقرار است:
![]()
در رابطه بالا NFE(t) برابر تعداد دفعات ارزیابی تابع هدف در تکرار tام است.
جلسه دوم: پیاده سازی بهینه سازی ازدحام ذرات در محیط متلب
هدف این جلسه پیاده سازی الگوریتم PSO می باشد. لذا جهت پیشگیری از برخورد با پیچیدگی های حل مسأله، مسأله بهینه سازی ساده sphere (کره) را در نظر می گیریم و با PSO آن را حل می کنیم. در خلال حل این مسأله، الگوریتم PSO پیاده خواهد شد:
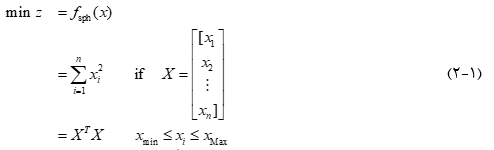
چنانچه بازه [xmin,xMax] شامل صفر باشد پاسخ بهینه برابر با xi=0⇒X=0 ⃗⇒z=0 خواهد بود.
نکته: پیاده سازی مسأله و روش (در اینجا همان الگوریتم PSO) همواره باید جدا از هم باشد و مسائل باید به گونه ای طراحی شوند که بتوان آنان را به هر الگوریتمی متصل و الگوریتم را مورد ارزیابی قرار داد.
برنامه را از نظر منطقی به ۵ قسمت تقسیم می کنیم تا بدانیم بخش های مختلف برنامه چه وظیفه ای برعهده دارند:
تعریف مسأله: مشخص کردن تابع هزینه، تعداد متغیرها، دامنه تغییرات متغیرها، ساختار پاسخ و …
معرفی تنظیمات الگوریتم: اندازه جمعیت، شرط توقف، پارامترهای الگوریتم و …
مقداردهی اولیه: جهت شروع اجرای الگوریتم به یک سری تنظیمات اولیه نیاز است.
حلقه اصلی: برای الگوریتم هایی که حالت تکراری و تکاملی دارند.
پس پردازش: گزارش گیری از نتایج، رسم تصاویر و نمودارها و ….
اکنون هریک از این مراحل به تشریح بررسی می شوند:
تعریف مسأله: پیاده سازی نهایی این قسمت به صورت زیر است:
در مورد خط کد زیر:
CostFunction=@(x) Sphere(x); % Cost Function
باید گفت علت تعریف تابع هزینه بدین گونه افزایش خوانایی کد است. در شاخه ریاضیات کاربردی توابع ارزیابی بسیاری جهت تست الگوریتم های بهینه سازی از جهت نرخ همگرایی، دقت، نااریبی و کارایی کلی به کار می روند. در این گونه از پیاده سازی تنها کافی است که نام تابع بهینه سازی در خط کد بالا عوض شود و هیچ نیازی به عوض کردن سایر قسمت های کد نیست. در واقع CostFunction در خط کد بالا متغیری از نوع function handle است.
VarSize=[1 nVar]; % Size of Decision Variables Matrix
این خط کد، نمایانگر ساختار پاسخ و نحوه چینش متغیرهای تصمیم در کنار هم می باشد.
معرفی تنظیمات الگوریتم: پیاده سازی نهایی این قسمت به صورت زیر است:
%% PSO Parameters
MaxIt=4000; % Maximum Number of Iterations
nPop=20; % Population Size (Swarm Size)
% w=1; % Inertia Weight
% wdamp=0.99; % Inertia Weight Damping Ratio
% c1=2; % Personal Learning Coefficient
% c2=2; % Global Learning Coefficient
% Constriction Coefficients
phi1=2.05;
phi2=2.05;
phi=phi1+phi2;
chi=2/(phi-2+sqrt(phi^2-4*phi));
w=chi; % Inertia Weight
wdamp=1; % Inertia Weight Damping Ratio
c1=chi*phi1; % Personal Learning Coefficient
c2=chi*phi2; % Global Learning Coefficient
% Velocity Limits
VelMax=0.1*(VarMax-VarMin);
VelMin=-VelMax;
VarSize=[1 nVar]; % Size of Decision Variables Matrix
VarMin=-10; % Lower Bound of Variables
VarMax= 10; % Upper Bound of Variables
اولین پارامتر مربوط به ماکزیمم تعداد تکرار یا شرط توقف است که در خط کد زیر مشخص شده است:
MaxIt=4000; % Maximum Number of Iterations
و خط کد زیر نیز اندازه جمعیت الگوریتم را مشخص می کند:
nPop=20; % Population Size (Swarm Size)
دیده می شود که جهت محاسبه ضرایب اینرسی، یادگیری شخصی و کلی دو راه پیش بینی شده است:
w=1;
wdamp=0.99;
c1=2;
c2=2;
این روش روشی ساده است که در آن ضرایب c1 و c2 برابر با بیشترین مقدار ممکن خود یعنی ۲ انتخاب شده اند. wdamp جهت رعایت اصل بالا بودن نرخ exploration در ابتدای اجرای الگوریتم و کاهش آن با گذر زمان اضافه شده به این صورت که در هر تکرار wdamp در مقدار قبلی w ضرب شده و باعث کاهش آن می گردد. به عنوان مثال در تکرار اول w=1، در تکرار دوم w=0.99، در تکرار سوم w=(0.99)2=0.9801، …. و نهایتا در تکرار ۴۰۰۰ام برابر w=(0.99)3999 است.
% Constriction Coefficients
phi1=2.05;
phi2=2.05;
phi=phi1+phi2;
chi=2/(phi-2+sqrt(phi^2-4*phi));
w=chi;
wdamp=1;
c1=chi*phi1;
c2=chi*phi2;
این روش که به constriction coefficients معروف است، توسط Clerc و Kennedy در سال ۲۰۰۲ معرفی شد. دو عدد مثبت φ۱ و φ۲ که مجموع آنان بیش از ۴ است را در نظر بگیرید:
![]()
سپس تعریف کنید:

اکنون می توان ضرایب اینرسی، یادگیری شخصی و کلی را به صورت زیر محاسبه کرد:

φ۱ و φ۲ همچنان که گفته شد می توانند هر عدد مثبتی که مجموع آنان بیش از ۴ باشد، باشند. اما Clerc و Kennedy اثبات نموده اند که در بین تمامی حالت های ممکن برای انتخاب φ۱ و φ۲ حالت بهینه عبارت است از:

در واقع در چنین حالتی تنظیمات ضرایب به گونه ای است که تعادل مناسبی بین exploration و exploitation برقرار می گردد و لذا تا انتهای اجرای الگوریتم نیازی به wdamp نداریم و می توانیم آن را حذف کرده یا همانند کد سمت راست، برابر ۱ قرار دهیم تا اثر کاهشی آن را در تکرارهای متوالی خنثی کنیم.
در نهایت در مورد خط کدهای زیر:
% Velocity Limits
VelMax=0.1*(VarMax-VarMin);
VelMin=-VelMax;
باید گفت که در PSO اصولا نمی توان گام های بزرگ را تحمل نمود، چون دقت را کاهش می دهند و لذا بایستی محدودیت سرعت قائل شویم. لذا سرعت بیشینه ای را تعریف می کنیم که بر اساس آن سرعت در هر بعد باید در بازه [Vmax ,Vmax-] باشد. البته طبق ادعای مطرح شده توسط Clerc و Kennedy در صورت استفاده از constriction coefficients اعمال شرط بیشینه سرعت لازم نیست ولی در اینجا چون می خواهیم تمامی موارد مرتبط با الگوریتم توضیح داده شوند، آن را نیز اضافه کرده ایم. طریقه تعیین VMax به صورت زیر است:
![]()
یعنی هر مولفه از بردار بیشینه سرعت متناسب با طول فضای جستجو در راستای همان مولفه می باشد. در اغلب اوقات فرض می شود که α=۰٫۰۵ یا α=۰٫۱٫
end
end
BestCost=zeros(MaxIt,1);
nfe=zeros(MaxIt,1);
particle=repmat(empty_particle,nPop,1);
GlobalBest.Cost=inf;
for i=1:nPop
% Initialize Position
particle(i).Position=unifrnd(VarMin,VarMax,VarSize);
% Initialize Velocity
particle(i).Velocity=zeros(VarSize);
% Evaluation
particle(i).Cost=CostFunction(particle(i).Position);
% Update Personal Best
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;
% Update Global Best
if particle(i).Best.Cost<GlobalBest.Cost
GlobalBest=particle(i).Best;
مقداردهی اولیه: پیاده سازی نهایی این قسمت به صورت زیر است:
در این بخش بایستی یک سری حافظه خالی ایجاد کنیم که در بخش بعدی توسط الگوریتم مورد استفاده قرار خواهد گرفت. اولین حافظه ای که باید ایجاد کنیم اعضای جمعیت و ویژگی های آنان است که در قطعه کد زیر انجام گرفته است:
empty_particle.Position=[];
empty_particle.Cost=[];
empty_particle.Velocity=[];
empty_particle.Best.Position=[];
empty_particle.Best.Cost=[];
طبق دیاگرام زیر میدانیم هر ذره دارای چهار خاصیت است که یکی از این خواص خود به دو زیر خاصیت تقسیم می شود:
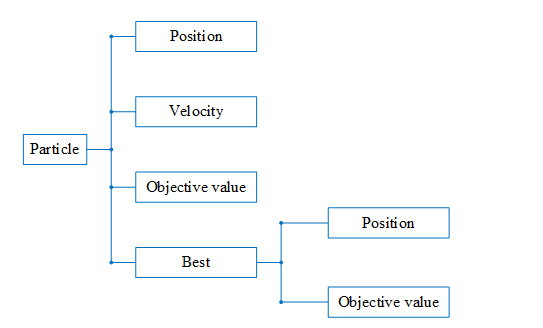
چنین ساختاری را در متلب با نوع داده struct پیاده می کنیم. در پنج خط کد نوشته شده در بالا empty_particle یک struct است که دارای چهار field می باشد. فیلد چهارم خود یک struct است که دارای دو field می باشد. خاصیت Best قرار است بهترین خاطره شخصی ذره را در خود ذخیره کند. حال از ذرات بالا، به تعداد npop نیاز داریم لذا از تابع repmat استفاده کرده، این تعداد empty_particle می سازیم و داخل آرایه ای به نام particle قرار می دهیم. در واقع particle یک ماتریس npop×۱ است که هریک از عضوهای آن از نوع struct می باشند.
particle=repmat(empty_particle,nPop,1);
یک struct به نام GlobalBest هم ساخته می شود. GlobalBest درست همانند Best بوده و دارای دو فیلد Position و Cost است. از آنجایی که در حال کمینه یابی هستیم مقدار اولیه Cost مربوط به GlobalBest را برابر با بدترین حالت ممکن یعنی +∞ می گیریم.
GlobalBest.Cost=inf;
نکته: چنانچه در حالت بیشینه یابی باشیم، بدترین حالت ممکن -∞ است. البته همانطور که می دانیم همواره می توان مسائل بیشینه یابی را با ضرب عدد منفی در تابع هدف یا معکوس کردن آن به مسائل کمینه یابی تبدیل کرد. لذا الگوریتم به همین شکل پیاده سازی شده کنونی برای مسائل بیشینه یابی نیز قابل استفاده است.
اکنون اعضای جمعیت باید با مقادیر تصادفی مقداردهی اولیه شوند:
for i=1:nPop
% Initialize Position
particle(i).Position=unifrnd(VarMin,VarMax,VarSize);
برای ایجاد مقادیر تصادفی از تابع unifrnd = uniform random با توزیع یکنواخت استفاده می شود. چون توزیع یکنواخت تنها توزیعی است که هیچ گونه بایاسی به هیچ سمتی ندارد.
سرعت اولیه ذرات را برابر با بردار صفر در نظر می گیریم:
% Initialize Velocity
particle(i).Velocity=zeros(VarSize);
به محض ایجاد فرد جدیدی از جمعیت یا ذره جدیدی از توده باید آن را ارزیابی کنیم. یعنی مقدار تابع هزینه برای آن محاسبه و در شمار ویژگی های فرد یا ذره قرار گیرد. لذا داریم:
% Evaluation
particle(i).Cost=CostFunction(particle(i).Position);
در حال حاضر ذره تنها یک تجربه داشته است. لذا موقعیت و هزینه فعلی آن به عنوان بهترین خاطره شخصی ثبت می شود:
% Update Personal Best
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;
همین جا در حین مقداردهی اولیه npop ذره موجود، چک می کنیم تا GlobalBest را با بهترین ذره اولیه جایگزین کنیم.
% Update Global Best
if particle(i).Best.Cost<GlobalBest.Cost
GlobalBest=particle(i).Best;
end
دقت شود که چون در ابتدای کار GlobalBest را برابر +∞ قرار داده ایم، شرط بالا حتما برای اولین ذره برقرار است و برای npop-1 ذره باقیمانده فقط در مواردی وارد if می شویم که cost متناظر با ذره از GlobalBest.Cost کوچکتر باشد.
نکته: دقت شود که کد بالا را می توان به صورت زیر نیز نوشت:
% Update Global Best
if particle(i).Best.Cost<GlobalBest.Cost
GlobalBest.Position=particle(i).Best.Position;
GlobalBest.Cost=particle(i).Best.Cost;
end
ولی چون GlobalBest و Particle(i).Best هر دو structure هایی با دو فیلد Position و Cost هستند، یعنی از یک جنس می باشند، نوشتن دو خط داخل بلوک if به صورت تک خط زیر اشکالی ندارد:
GlobalBest=particle(i).Best;
یعنی خودبه خود هر فیلد در یک ساختار (structure) با متناظر خود در ساختار (structure) دیگر جایگزین می شود.
اگر بخواهیم نمودار همگرایی یا نمودار کاهش هزینه ها را ترسیم کنیم بایستی در هر تکرار بهترین cost را که تا آن تکرار پیدا شده، داشته باشیم. لذا باید ماتریس یا برداری داشته باشیم که در هر تکرار GlobalBest مربوط را در آن ذخیره کنیم. پس ماتریسی با اندازه MaxIt تشکیل می دهیم:
BestCost=zeros(MaxIt,1);
از سوی دیگر اگر بخواهیم نمودار هزینه را نسبت به nfe ترسیم کنیم، باید nfe مربوط را در هر تکرار داشته باشیم. لذا ماتریسی نیز با اندازه MaxIt جهت ذخیره nfe در هر تکرار تشکیل می دهیم:
nfe=zeros(MaxIt,1);
البته می دانیم رابطه nfe با iteration در الگوریتم PSO به صورت زیر است:
![]()
حلقه اصلی: پیاده سازی نهایی این قسمت به صورت زیر است:
%% PSO Main Loop
for it=1:MaxIt
for i=1:nPop
% Update Velocity
particle(i).Velocity = w*particle(i).Velocity …
+c1*rand(VarSize).*(particle(i).Best.Position-particle(i).Position) …
+c2*rand(VarSize).*(GlobalBest.Position-particle(i).Position);
% Apply Velocity Limits
particle(i).Velocity = max(particle(i).Velocity,VelMin);
particle(i).Velocity = min(particle(i).Velocity,VelMax);
% Update Position
particle(i).Position = particle(i).Position + particle(i).Velocity;
% Velocity Mirror Effect
IsOutside=(particle(i).Position<VarMin | particle(i).Position>VarMax);
particle(i).Velocity(IsOutside)=-particle(i).Velocity(IsOutside);
% Apply Position Limits
particle(i).Position = max(particle(i).Position,VarMin);
particle(i).Position = min(particle(i).Position,VarMax);
% Evaluation
particle(i).Cost = CostFunction(particle(i).Position);
% Update Personal Best
if particle(i).Cost<particle(i).Best.Cost
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;
% Update Global Best
if particle(i).Best.Cost<GlobalBest.Cost
GlobalBest=particle(i).Best;
end
end
end
BestCost(it)=GlobalBest.Cost;
nfe(it)=NFE;
disp([‘Iteration ‘ num2str(it) ‘: NFE = ‘ num2str(nfe(it)) ‘, Best Cost = ‘…
num2str(BestCost(it))]);
w=w*wdamp;
end
این حلقه بایستی به تعداد MaxIt تکرار شود و سرعت و موقعیت تمامی اعضای جمعیت در هر تکرار به روز شود. دیده می شود که کد مربوط به به روز کردن سرعت از همان معادله (۱-۱) تبعیت می کند.
% Update Velocity
particle(i).Velocity = w*particle(i).Velocity …
+c1*rand(VarSize).*(particle(i).Best.Position-particle(i).Position) …
+c2*rand(VarSize).*(GlobalBest.Position-particle(i).Position);
کد rand(VarSize) و همچنین اپراتور .* نشان می دهد که هریک از مولفه های بردار جابجایی
(particle(i).Best.Position-particle(i).Position)
متناظر با (x(i,Personal best)-xi (t)) و یا بردار جابجایی
(GlobalBest.Position-particle(i).Position)
متناظر با (x(Global best)-xi (t)) باید در عدد تصادفی جداگانه ای ضرب شوند.
بلافاصله پس از به روزکردن سرعت ذره باید بررسی کنیم که سرعت آن بیشتر از مقادیر بیشینه و کمینه مشخص شده در معادله ۷-۲ نباشد. چنانچه سرعت بیشتر از بیشینه مقدار ممکن باشد، آن را با بیشینه مقدار ممکن جایگزین می کنیم و چنانچه کمتر از کمینه مقدار ممکن باشد، آن را با کمینه مقدار ممکن جایگزین می کنیم.
در خط کد زیر سرعت را برابر با بیشینه بین particle(i).Velocity و VelMin لحاظ کرده ایم، یعنی چنانچه سرعت کوچکتر از مقدار کمینه باشد، مقدار کمینه از تابع max خارج خواهد شد.
particle(i).Velocity = max(particle(i).Velocity,VelMin);
و در خط کد زیر سرعت را برابر با کمینه بین particle(i).Velocity و VelMax لحاظ کرده ایم، یعنی چنانچه سرعت بزرگتر از مقدار بیشینه باشد، مقدار بیشینه از تابع min خارج خواهد شد.
particle(i).Velocity = min(particle(i).Velocity,VelMax);
پس از به روز کردن سرعت و بررسی اینکه سرعت به روز شده خارج از محدوده از پیش تعیین شده نباشد، بایستی با استفاده از آن موقعیت ذرات به روز شود:
% Update Position
particle(i).Position = particle(i).Position + particle(i).Velocity;
اثر آینه ای (اثر انعکاسی): این امکان وجود دارد که پس از به روز کردن موقعیت ذره از فضای جستجو که در قسمت تعریف مسأله توسط پارامترهای VarMin و VarMax خارج شویم. در چنین صورتی باید سرعت را در راستای مولفه هایی از بردار موقعیت که خارج از فضای جستجو می باشند قرینه کنیم.
% Velocity Mirror Effect
IsOutside=(particle(i).Position<VarMin | particle(i).Position>VarMax);
particle(i).Velocity(IsOutside)=-particle(i).Velocity(IsOutside);
یکی از ویژگی های متلب اندیس گذاری شرطی است. در خط اول از کد بالا، برداری باینری هم اندازه با بردار موقعیت تشکیل می شود که به ازای مولفه هایی از بردار موقعیت که خارج از بازه [VarMin, VarMax] باشد، برابر ۱ و به ازای سایر مولفه ها برابر صفر است. این بردار باینری در خط دوم به عنوان اندیس برای بردار سرعت استفاده شده است، تا فقط مولفه هایی که اندیس آنان برابر ۱ است، قرینه گردند.
اثر آینه ای را می توان بدین صورت توضیح داد:
میز بیلیاردی را در نظر بگیرید که ضربه ای از طرف چوب بیلیارد به گوی وارد می شود، گوی به سمت لبه میز حرکت می کند ولی لبه برآمده، مانع از خروج توپ می شود و با برخورد به لبه توپ باز می گردد. پس از اعمال شرط آینه ای، موقعیت را اصلاح می کنیم تا مانع از خروج ذره از فضای جستجو شویم:
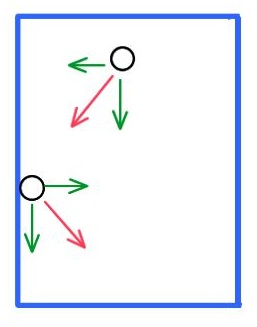
% Apply Position Limits
particle(i).Position = max(particle(i).Position,VarMin);
particle(i).Position = min(particle(i).Position,VarMax);
همچنانکه در قسمت مقداردهی اولیه گفته شد، به محض ایجاد فرد جدیدی از جمعیت یا ذره جدیدی از توده باید آن را ارزیابی کنیم، اکنون هم می گوییم به محض تغییر موقعیت فردی از جمعیت یا ذره ای از توده باید موقعیت جدید را ارزیابی و خاصیت cost آن را تنظیم کنیم. لذا:
% Evaluation
particle(i).Cost = CostFunction(particle(i).Position);
سپس باید دید آیا ذره توانسته است رکورد خود را جابجا کند یا خیر و اگر موفق به جابجا کردن رکورد خود شده است، آیا توانسته است رکورد جمعی را نیز جابجا کند یا خیر؟
% Update Personal Best
if particle(i).Cost<particle(i).Best.Cost
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;
% Update Global Best
if particle(i).Best.Cost<GlobalBest.Cost
GlobalBest=particle(i).Best;
end
end
در اینجا حلقه زیر بسته می شود:
for i=1:nPop
% Update Velocity
% Apply Velocity Limits
% Update Position
% Velocity Mirror Effect
% Apply Position Limits
% Evaluation
% Update Personal Best
% Update Global Best
end
یعنی عملیات به روز رسانی سرعت، اعمال حدود به سرعت، به روز رسانی موقعیت، اعمال اثر آینه ای، اعمال حدود به موقعیت، ارزیابی موقعیت جدید و بررسی جابجا شدن یا نشدن رکوردهای شخصی و جمعی برای تمامی ذرات در یک تکرار انجام می شود. پیش از رفتن به تکرار بعدی اقداماتی انجام می گیرد:
رکورد جمعی ذرات را به عنوان بهترین رکوردی که تا تکرار کنونی به آن رسیده ایم، قرار می دهیم:
BestCost(it)=GlobalBest.Cost;
تعداد دفعات ارزیابی تابع هدف (NFE) تا تکرار کنونی را ذخیره می کنیم:
nfe(it)=NFE;
یادآوری می شود که ماتریس های nfe و BestCost پیش تر در قسمت مقداردهی اولیه با اندازه MaxIt×۱ ایجاد شدند.
خط کد زیر بهترین مقدار تابع هزینه و تعداد دفعات ارزیابی آن تا تکرار کنونی را به علاوه آن تکرار نمایش خواهد داد:
disp([‘Iteration ‘ num2str(it) ‘: NFE = ‘ num2str(nfe(it)) ‘, Best Cost = ‘…
num2str(BestCost(it))]);
نمونه ای از این نمایش به صورت زیر است:
Iteration 61: NFE = 1240, Best Cost = 0.00012993
در نهایت قبل از بستن حلقه زیر
for it=1:MaxIt
end
یعنی پیش از رفتن به تکرار بعدی باید w را در wdamp ضرب کنیم. زیرا همانطور که گفته شد در ابتدای الگوریتم نرخ exploration بایستی بالا باشد و رفته رفته از این نرخ کاسته و نرخ exploitation را افزایش می دهیم.
w=w*wdamp;
پس پردازش: پیاده سازی نهایی این قسمت به صورت زیر است:
%% Results
figure;
%plot(nfe,BestCost,’LineWidth’,2);
semilogy(nfe,BestCost,’LineWidth’,2);
xlabel(‘NFE’);
ylabel(‘Best Cost’);
با استفاده از قطعه کد زیر یک فضای جدید جهت رسم ایجاد می کنیم:
figure;
قطعه کد زیر که البته به صورت کامنت درآمده و اجرا نخواهد شد ترسیم را انجام می دهد به این صورت که مولفه x نقاط روی نمودار نشانگر nfe و مولفه y نقاط نشان گر BestCost است.
%plot(nfe,BestCost,’LineWidth’,2);
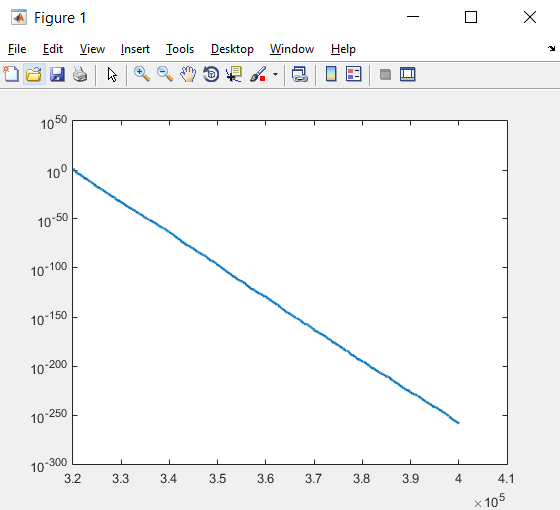
اگر این قطعه کد اجرا شود نتیجه به صورت زیر است:

با توجه به اینکه مقادیر BestCost در این مسأله از مرتبه ۱۰۲ تا مرتبه -۲۵۶ ۱۰ متغیر است، لازم است مقیاس بندی محور y به صورت لگاریتمی باشد تا بتواند تغییرات را بهتر نمایش دهد. تابع semilogy در خط کد زیر جهت این کار به کار می رود:
semilogy(nfe,BestCost,’LineWidth’,2);
در نهایت توسط کدهای زیر، محورهای x و y را برچسب گذاری می کنیم.
xlabel(‘NFE’);
ylabel(‘Best Cost’);
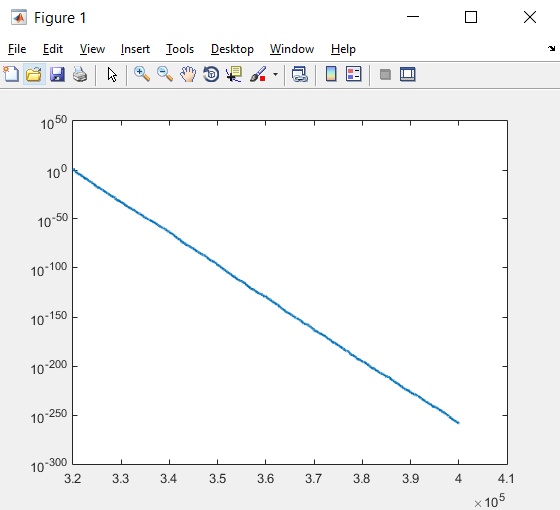
نکته: LineWidth خاصیتی مربوط به ضخامت منحنی که جهت ترسیم به کار می رود، می باشد. اگر LineWidth را تنظیم نکنیم، متلب به صورت پیش فرض، آن را برابر ۵/۰ در نظر می گیرد. در شکل سمت چپ، نمودار بالا را به ازای LineWidth=10 و در شکل سمت راست، این نمودار را که بدون تنظیم LineWidth رسم شده است، می بینید.
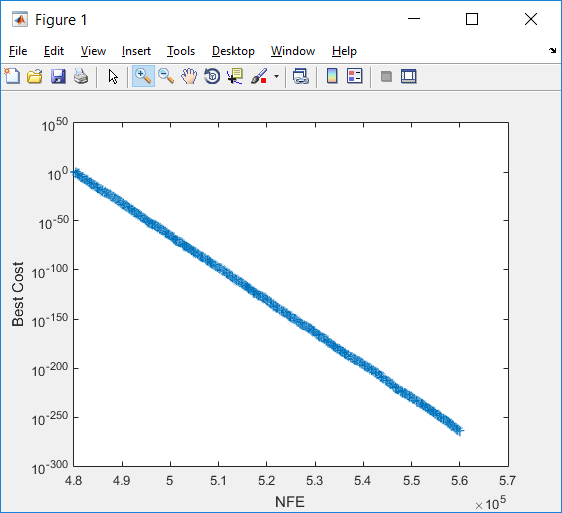
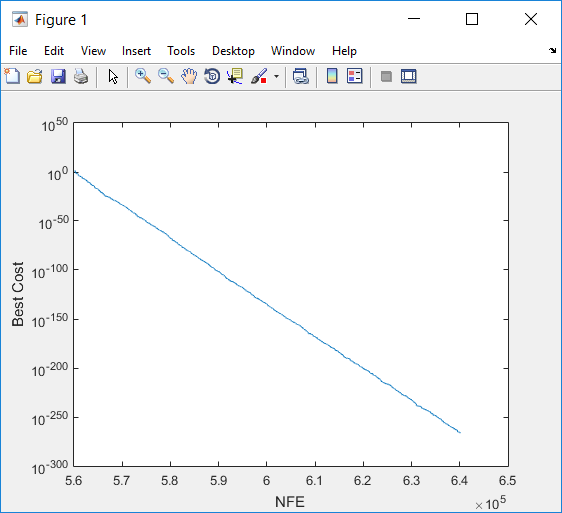
در نهایت بایستی تابع Sphere را که در قسمت تعریف مسأله به کار بردیم و در هر تکرار و برای هر ذره با فراخوانی CostFunction (تابع هدف) آن را احضار می کنیم، تعریف کنیم. این تابع را می توان در فایل Sphere.m تعریف کرد و در همان دایرکتوری که pso.m را ذخیره کرده ایم، قرار داد.
function z=Sphere(x)
global NFE;
if isempty(NFE)
NFE=0;
end
NFE=NFE+1;
z=sum(x.^2);
end
در مورد خط کد زیر که هم در فایل pso.m و در قسمت تعریف مسأله و هم در فایل Sphere.m نوشته شد، بایستی گفت:
global NFE;
به مقدار متغیر NFE هم در workspace (فضای کاری) مربوط به تابع Sphere و هم در فضای کاری برنامه pso.m نیاز داریم، لذا بایستی در ابتدای هر دو فایل این متغیرها را به عنوان متغیر جهانی (global) تعریف کنیم. این متغیر وقتی اولین بار تابع Sphere را احضار می کنیم خالی است و نمی توان یک متغیر خالی را در طرف راست = قرار داد. یعنی در حالتی که NFE خالی باشد، نمی توان خط کد زیر را نوشت:
NFE=NFE+1;
ولی در دفعات بعدی احضار تابع Sphere متغیر NFE مقدار دارد و می توان خط کد بالا را برای آن به کار برد و از طرفی چون NFE شمارنده تعداد احضار، تابع هدف است نباید در دفعات بعدی احضار، مقدار آن برابر صفر شود. لذا بلوک if…end را به صورت زیر می نویسیم تا فقط در اولین احضار تابع هدف وارد بلوک شده و شمارنده را صفر کنیم.
if isempty(NFE)
NFE=0;
end
اگر به قسمت تعریف مسأله در فایل pso.m مراجعه کنیم. دیده می شود که بعد از کد
global NFE;
کد زیر قرار گرفته است:
NFE=0;
وجود این خط کد الزامی است. و در صورت عدم وجود این خط کد، اگر بخواهیم دوبار برنامه (script)، pso را اجرا کنیم، ممکن است تعداد دفعات ارزیابی تابع هدف اشتباه شمرده شود.
در نهایت توسط کد زیر مقدار تابع هدف که همان رابطه ![]() در ابتدای فصل است، مقدار تابع هدف را محاسبه و به عنوان خروجی تابع برمیگردانیم.
در ابتدای فصل است، مقدار تابع هدف را محاسبه و به عنوان خروجی تابع برمیگردانیم.
z=sum(x.^2);
جلسه سوم: حل مسأله دیسپاچینگ اقتصادی
از این جلسه به بعد، الگوریتم PSO را که در جلسه قبل نوشته شد جهت حل مسائل مختلف به کار می بریم. یعنی با استفاده از نکته گفته شده در جلسه قبل:
نکته: پیاده سازی مسأله و روش (در اینجا همان الگوریتم PSO) همواره باید جدا از هم باشد و مسائل باید به گونه ای طراحی شوند که بتوان آنان را به هر الگوریتمی متصل و الگوریتم را مورد ارزیابی قرار داد.
از این پس پیاده سازی مسائل را مورد بررسی قرار می دهیم و کدنویسی معطوف به پیاده سازی مسأله است و سپس مسأله کدشده را به الگوریتم پیاده سازی شده در جلسه قبل متصل می کنیم. البته ممکن است به اعمال تغییرات جزئی در فایل PSO.m نیاز باشد که مورد اشاره قرار خواهد گرفت.
مسأله Economic Dispatching از جمله مسائل مهم حوزه مهندسی قدرت و مدیریت انرژی است که البته شکل اصلی آن بسیار پیچیده است. در اینجا ما شکل ساده شده ای را که در آن همه نیروگاه ها (منابع) انرژی از یک نوع بوده و همه نیروگاه ها فعال هستند (قرار نیست در مورد احداث یا عدم احداث نیروگاه تصمیم گرفته شود) آن هم در لحظه ای از زمان در نظر می گیریم.
فرض شود n منبع تولید انرژی داریم که توان تولیدی هرکدام از آنان برابر Pi هست. (i∈{۱,۲,…,n})
هر نیروگاه دارای حداقل و حداکثر توان تولیدی مشخص است. زیرا هیچ نیروگاهی نمی تواند غیرفعال باشد و حتی اگر در کمترین حالت کار کند، باید حداقل توان مشخصی را جهت توجیه پذیری اقتصادی ساخت نیروگاه تامین کند (Pimin). همچنین ظرفیت هر نیروگاه محدود بوده و حداکثر توانی که می تواند تولید کند (Pimax) مشخص است. (Pi^min<Pi<Pi^max)
کارکرد هریک از منابع مستلزم پرداخت هزینه است و هر چقدر توان تولیدی منبع بیشتر باشد، هزینه بیشتری پرداخت خواهیم کرد که البته شیب افزایش قیمت با افزایش توان تولیدی کاهش می یابد. لذا می توان فرض کرد که رابطه توان تولیدی نیروگاه i ام (Pi) با هزینه نیروگاه i ام (Ci) به صورت یک سهمی (چندجمله ای درجه دو) با تقعر به سمت پایین باشد.
![]()
با توجه به جهت تقعر داریم : a2i<0
همچنین حتی در صورتی که توان تولیدی یک نیروگاه صفر باشد باز هم هزینه ثابت a0i برای هر نیروگاه وجود دارد. این هزینه می تواند مواردی مثل هزینه حفاظت از تاسیسات و … باشد. لذا داریم a0i>0
همچنین چنانچه بار مورد نیاز از شبکه در یک لحظه برابر PL باشد. مجموع نیروگاه های موجود در شبکه بایستی بتواند این بار مورد نیاز را تامین کند. یعنی مجموع توان تولیدی نیروگاه ها در این لحظه بایستی برابر PL باشد.

توانی که هر نیروگاه بایستی تامین کند را به قسمی بیابید (متغیرهای تصمیم همان Pi است) که مجموع هزینه ها کمینه گردد. لذا تابع هدف که باید کمینه گردد، عبارت است از:
![]()
به طور کلی جهت حل مسائل باید ۴ مرحله را پشت سر بگذاریم:
۱) ایجاد مکانیزمی برای برای تولید، ذخیره سازی و فراخوانی اطلاعات مدل
۲) ایجاد مکانیزمی برای تولید پاسخ تصادفی
۳) پیاده سازی تابع هزینه و برآورد قیدها
۴) اتصال تابع هزینه به الگوریتم بهینه سازی
مرحله اول: ایجاد مکانیزمی برای برای تولید، ذخیره سازی و فراخوانی اطلاعات مدل
برای این مرحله تابعی به نام CreateModel را تعریف می کنیم. هدف از این تابع ایجاد یک مسأله نمونه و ذخیره سازی پارامترهای آن در ساختاری به نام model است. تا در هر زمان که به داده های مسأله نیاز داشتیم، آنان را از ساختار model بازیابی کنیم. پیاده سازی نهایی این تابع به صورت زیر است:
function model=CreateModel()
pmin=[511 804 501 747 514 655 555 705];
pmax=[1516 1924 1765 1611 1981 1792 2174 1965];
a0=[8736 5849 8343 9123 6340 6833 5951 6382];
a1=[8 7 8 6 6 9 6 9];
a2=[-0.1573 -0.1430 -0.2574 -0.1128 -0.1344 -0.2375 -0.1631 -0.1784]*1e-4;
N=numel(pmin);
PL=10000;
model.N=N;
model.pmin=pmin;
model.pmax=pmax;
model.a0=a0;
model.a1=a1;
model.a2=a2;
model.PL=PL;
end
فرض کنید ۸ نیروگاه داشته باشیم. مهم ترین پارامترهایی که بایستی تعریف شود، حد پایین و بالای توان تولیدی هر یک از نیروگاه ها است که توسط دو خط کد زیر صورت می گیرد:
pmin=[511 804 501 747 514 655 555 705];
pmax=[1516 1924 1765 1611 1981 1792 2174 1965];
ماتریس اول با استفاده از تولید اعداد صحیح تصادفی در بازه [۴۰۰,۹۰۰] و ماتریس دوم با استفاده از تولید اعداد صحیح تصادفی در بازه [۱۴۰۰,۲۲۰۰] بدست آمده است. برای تولید اعداد تصادفی صحیح از تابع randi استفاده می کنیم.
برای آنکه تعداد نیروگاه ها را بدست آوریم، کافی است تعداد اعضای هر یک از ماتریس های بالا را بدست آوریم. برای بدست آوردن تعداد اعضای یک ماتریس از تابع numel که مخفف number of elements می باشد، استفاده می کنیم:
N=numel(pmin);
می دانیم PL بایستی بزرگتر از مجموع کران پایین توان تولیدی (۴۹۹۲) و کوچکتر از مجموع کران بالای توان تولیدی (۱۴۷۲۸) باشد. لذا می توانیم آن را برابر با ۱۰۰۰۰ فرض کنیم.
PL=10000;
مربوط به هر نیروگاه را از طریق تولید اعداد تصادفی صحیح در بازه اعداد بین ۵۰۰۰ تا ۹۹۰۰ می یابیم.
a0=[8736 5849 8343 9123 6340 6833 5951 6382];
از سوی دیگر می دانیم مشتق معادله (۳-۱) و بنابراین طول راس سهمی عبارت است از:
![]()
از سوی دیگر، همانطور که گفته شد، تنها نیمه اول و صعودی سهمی را در نظر می گیریم، لذا برای هر نیروگاه باید داشته باشیم:
![]()
لذا باید a2i یک عدد منفی بسیار نزدیک به صفر و a1i که عددی مثبت و بسیار بزرگتر از صفر باشد، تا کسر
![]()
تا حد امکان بزرگ شود.
ماتریس a1 را از طریق تولید اعداد صحیح تصادفی بین ۵ و ۹ می سازیم.
a1=[8 7 8 6 6 9 6 9];
ماتریس a2 را با کد a2=-unifrnd(1e-5,3e-5,1,8) می توان تولید کرد.
a2=[-0.1573 -0.1430 -0.2574 -0.1128 -0.1344 -0.2375 -0.1631 -0.1784]*1e-4;
سپس اطلاعات را به صورت فیلدهایی در ساختار model ذخیره کرده و به صورت خروجی تابع برمیگردانیم.
model.N=N;
model.pmin=pmin;
model.pmax=pmax;
model.a0=a0;
model.a1=a1;
model.a2=a2;
model.PL=PL;
مرحله دوم: ایجاد مکانیزمی برای تولید پاسخ تصادفی
راه حل تصادفی ایجاد شده جهت این مسأله بایستی ۸ عدد حقیقی باشد که هرکدام کران بالا و پایین مشخص دارند. برای اینکار کافی است ورودی های اول و دوم تابع unifrnd که نشان دهنده حد بالا و پایین متغیرهای تصمیم هستن ماتریس های با اندازه یکسان باشند. برای این منظور تابع زیر نوشته شده است:
function p=CreateRandomSolution(model)
pmin=model.pmin;
pmax=model.pmax;
p=unifrnd(pmin,pmax);
end
نکته: متغیرهای VarMin و VarMax در قسمت تعریف مسأله از پیاده سازی الگوریتم PSO را می توان به صورت متغیرهایی برداری تعریف کرد. یعنی چنانچه در الگوریتم PSO با n متغیر حقیقی سر و کار داشته باشیم که هرکدام حد بالا و پایین متفاوتی دارند، می توانیم دو ماتریس با تعداد n المان تعریف و در یکی حد پایین تمامی متغیرها و در دیگری حد بالای تمامی متغیرها را بنویسیم.
مرحله سوم: پیاده سازی تابع هزینه و برآورد قیدها
شکل نهایی تابعی که بدین منظور نوشته شده است، به صورت زیر است:
function [z sol]=MyCost(p,model)
global NFE;
if isempty(NFE)
NFE=0;
end
NFE=NFE+1;
a0=model.a0;
a1=model.a1;
a2=model.a2;
PL=model.PL;
%c=zeros(size(p));
%for i=1:N
% c(i)=a0(i)+a1(i)*p(i)+a2(i)*p(i)^2;
%end
% Vectorized version of the previous loop
c=a0+a1.*p+a2.*p.^2;
v=abs(sum(p)/PL-1);
beta=2;
z=sum(c)*(1+beta*v);
sol.p=p;
sol.pTotal=sum(p);
sol.c=c;
sol.cTotal=sum(c);
sol.v=v;
sol.z=z;
end
توضیحات مربوط به خطوط کد ذیل مشابه توضیحات پیشین در جلسه دوم است.
global NFE;
if isempty(NFE)
NFE=0;
end
با توجه به روابط (۳-۱)، (۳-۲) و (۳-۳) می دانیم برای محاسبه هزینه به a0، a1، a2 و PL نیاز داریم. لذا این چهار کمیت را از ساختار model که به عنوان ورودی تابع است، استخراج میکنیم.
a0=model.a0;
a1=model.a1;
a2=model.a2;
PL=model.PL;
طبق معادله (۳-۱)، ci ها را ساخته و در بردار c ذخیره می کنیم:
c=a0+a1.*p+a2.*p.^2;
در اینجا بحثی فرعی پدید می آید که در زیر بدان پرداخته ایم.
تکنیک های حل مسأله بهینه سازی مقید
تعریف جریمه (penalty) برای عدم برآورده شدن قیدها
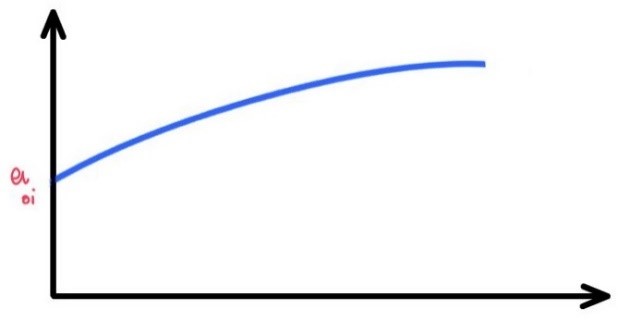
به عنوان مثال فرض کنید با قید g≥g0 مواجهیم. تخطی یا جریمه بایستی در صورت برقرار بودن قید برابر صفر و در صورت عدم برقراری آن، مثبت باشد. لذا اگر تخطی را با v یعنی violation نشان دهیم، بایستی داشته باشیم:
![]()
مثبت بودن تخطی بدین خاطر است که بعدها این عدد، باید به عنوان جریمه به تابع هزینه اضافه شود و در صورت عدم برقراری قید مانع از کمینه شدن هزینه شود.
اما اندازه جریمه نیز بایستی منعکس کننده میزان تخلف و تخطی پیش آمده باشد.
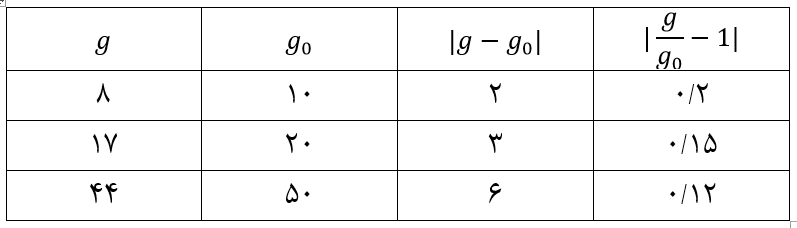
به عنوان مثال یک حالت جهت تعریف penalty می تواند به صورت زیر باشد:
![]()
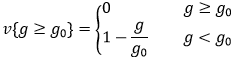
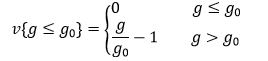
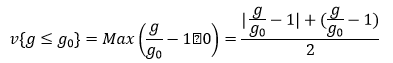
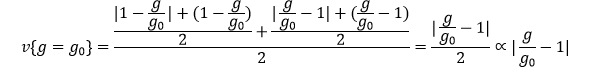
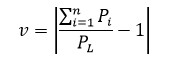

sol.pTotal=sum(p);
sol.c=c;
sol.cTotal=sum(c);
sol.v=v;
sol.z=z;
%% Problem Definition
global NFE;
NFE=0;
model=CreateModel();
CostFunction=@(p) MyCost(p,model); % Cost Function
nVar=model.N; % Number of Decision Variables
VarSize=[1 nVar]; % Size of Decision Variables Matrix
VarMin=model.pmin; % Lower Bound of Variables
VarMax=model.pmax; % Upper Bound of Variables
تعریف مسأله: تغییراتی در قسمت تعریف مسأله جلسه دوم به شرح زیر ایجاد خواهد شد:
ابتدا داده های مورد نیاز مسأله با استفاده از تابع CreateModel ساخته شده است.
model=CreateModel();
سپس تابع MyCost به عوض Sphere در متغیر CostFunction که از نوع Function handle است، جایگزین شده است.
CostFunction=@(p) MyCost(p,model); % Cost Function
سایر اطلاعات مسأله همچون تعداد متغیرهای تصمیم گیری (تعداد نیروگاه ها)، و حد بالا و پایین مقادیر متغیرهای تصمیم گیری را از ساختار model بیرون می آوریم.
nVar=model.N; % Number of Decision Variables
VarSize=[1 nVar]; % Size of Decision Variables Matrix
VarMin=model.pmin; % Lower Bound of Variables
arMax=model.pmax; % Upper Bound of Variables
مقداردهی اولیه: تغییراتی در قسمت مقدار دهی اولیه جلسه دوم به شرح زیر ایجاد خواهد شد:
%% Initialization
empty_particle.Position=[];
empty_particle.Cost=[];
empty_particle.Sol=[];
empty_particle.Velocity=[];
empty_particle.Best.Position=[];
empty_particle.Best.Cost=[];
empty_particle.Best.Sol=[];
particle=repmat(empty_particle,nPop,1);
GlobalBest.Cost=inf;
for i=1:nPop
% Initialize Position
particle(i).Position=CreateRandomSolution(model);
% Initialize Velocity
particle(i).Velocity=zeros(VarSize);
% Evaluation
[particle(i).Cost, particle(i).Sol]=…
CostFunction(particle(i).Position);
% Update Personal Best
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;
particle(i).Best.Sol=particle(i).Sol;
% Update Global Best
if particle(i).Best.Cost<GlobalBest.Cost
GlobalBest=particle(i).Best;
end
end
BestCost=zeros(MaxIt,1);
nfe=zeros(MaxIt,1);
از آنجایی که تابع هزینه دارای دو خروجی cost و Sol است، هر فرد پس از هر بار ارزیابی باید بتواند Cost و Sol مربوط به خود را ذخیره کند. همچنین فرد باید بتواند Best Cost و Best Sol خود را نیز ذخیره کند. لذا با استفاده از کدهای زیر، به هر فرد ویژگی Sol و به بهترین خاطره فرد یعنی خصیصه Best آن نیز ویژگی Sol را اضافه می کنیم.
empty_particle.Sol=[];
empty_particle.Best.Sol=[];
نباید فراموش شود اکنون که خصیصه Best هر فرد دارای سه فیلد (ویژگی) است، GlobalBest یعنی بهترین خاطره جمیع افراد نیز دارای سه فیلد خواهد بود.
جهت تولید پاسخ تصادفی از تابع CreateRandomSolution استفاده می کنیم.
% Initialize Position
particle(i).Position=CreateRandomSolution(model);
از آنجایی که تابع MyCost دارای دو خروجی است، قسمت ارزیابی فرد به صورت زیر تغییر خواهد کرد:
% Evaluation
[particle(i).Cost, particle(i).Sol]=…
CostFunction(particle(i).Position);
دقت شود که با توجه به خط کد
CostFunction=@(p) MyCost(p,model); % Cost Function
و آنچه داخل @() آمده است، متغیر CostFunction که از نوع function handle است فقط دارای یک آرگومان ورودی p مخفف position است. لذا هنگام ارزیابی تنها کافی است خصیصه مکان ذره particle(i).Position را به CostFunction پاس کنیم. از آنجایی که CostFunction یک handle است که اشاره به MyCost دارد. خود به خود علاوه بر position ،model نیز به MyCost پاس شده و این تابع فراخوانی شده، خروجی را تولید می کند. در قسمت بعدی خصیصه Sol مربوط به بهترین خاطره ذره را علاوه بر دو خصیصه دیگر به روز می کنیم.
particle(i).Best.Sol=particle(i).Sol;
حلقه اصلی: تغییراتی در قسمت حلقه اصلی جلسه دوم به شرح زیر ایجاد خواهد شد:
%% PSO Main Loop
for it=1:MaxIt
for i=1:nPop
% Update Velocity
particle(i).Velocity = w*particle(i).Velocity …
+c1*rand(VarSize).*(particle(i).Best.Position-particle(i).Position) …
+c2*rand(VarSize).*(GlobalBest.Position-particle(i).Position);
% Apply Velocity Limits
particle(i).Velocity = max(particle(i).Velocity,VelMin);
particle(i).Velocity = min(particle(i).Velocity,VelMax);
% Update Position
particle(i).Position = particle(i).Position + particle(i).Velocity;
% Velocity Mirror Effect
IsOutside=(particle(i).Position<VarMin | particle(i).Position>VarMax);
particle(i).Velocity(IsOutside)=-particle(i).Velocity(IsOutside);
% Apply Position Limits
particle(i).Position = max(particle(i).Position,VarMin);
particle(i).Position = min(particle(i).Position,VarMax);
% Evaluation
[particle(i).Cost, particle(i).Sol] = CostFunction(particle(i).Position);
% Update Personal Best
if particle(i).Cost<particle(i).Best.Cost
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;
particle(i).Best.Sol=particle(i).Sol;
% Update Global Best
if particle(i).Best.Cost<GlobalBest.Cost
GlobalBest=particle(i).Best;
end
end
end
BestCost(it)=GlobalBest.Cost;
nfe(it)=NFE;
disp([‘Iteration ‘ num2str(it) ‘: NFE = ‘ num2str(nfe(it)) ‘, Best Cost = ‘ num2str(BestCost(it))]);
w=w*wdamp;
end
تغییراتی که در این قسمت ایجاد می شود همانند قسمت پیشین است. یعنی فقط در نحوه فراخوانی تابع هزینه تغییر ایجاد شده به علاوه اینکه همانطور که گفته شد هر بار هنگام بروزرسانی خصیصه Cost بهترین خاطره فرد باید خصیصه Sol این بهترین خاطره نیز به روز شود.
% Evaluation
[particle(i).Cost, particle(i).Sol] = CostFunction(particle(i).Position);
% Update Personal Best
if particle(i).Cost<particle(i).Best.Cost
particle(i).Best.Position=particle(i).Position;
particle(i).Best.Cost=particle(i).Cost;
particle(i).Best.Sol=particle(i).Sol;
پس پردازش: تغییراتی در قسمت پس پردازش جلسه دوم به شرح زیر ایجاد خواهد شد:
%% Results
figure;
plot(nfe,BestCost,’LineWidth’,2);
xlabel(‘NFE’);
ylabel(‘Best Cost’);
تنها تغییری که در این قسمت ایجاد می شود این است که چون تغییرات هزینه ها در این مسأله لگاریتمی نیست، دیگر نیازی به استفاده از تابع semilogy نداریم و از تابع plot استفاده می کنیم.
مجموعه: اخبار و تازه ها




 (3 votes, average: 4٫67 out of 5)
(3 votes, average: 4٫67 out of 5)
سلام بسیار ممنون .ذکات دانش انتشار دادن آن است. انشالله همواره موفق باشید و بر قله علم پایدار بمانید