در «علم داده» ( Data Science)، افراد اغلب درباره چگونگی استفاده از داده‌ها برای انجام پیش‌بینی برای نقاط داده جدید می‌اندیشند. گاهی اوقات، به جای انجام پیش‌بینی، هدف دسته‌بندی داده‌ها به «خوشه‌های» (Clusters) گوناگون است. به این کار، «یادگیری نظارت شده» (Supervised Learning) گفته می‌شود. برای درک بهتر موضوع، فرض می‌شود که فردی در یک مرکز فروش پیتزا قرار دارد و از او خواسته شده که ویژگی‌ای در نرم‌افزار مدیریت سفارشات پیتزا ایجاد کند که مدت زمان تحویل را برای مشتریان پیش‌بینی کند. به منظور انجام این کار، یک مجموعه داده به فرد داده می‌شود که مدت زمان‌های تحویل، فاصله‌هایی که غذاها تحویل داده شده‌اند، روز هفته، زمان در روز، کارکنان در دسترس و حجم فروش‌ها برای چندین تحویل برای گذشته در آن قرار دارد. از این داده‌های، می‌توان برای زمان‌های تحول آینده پیش‌بینی انجام داد. این یک مثال خوب از یادگیری نظارت شده است.

اکنون، فرض می‌شود که پیتزا فروشی قصد ارسال کوپن‌های هدفمند را به مشتریان دارد. فروشگاه قصد دارد مشتریان خود را به چهار گروه تقسیم کند که عبارتند از خانواده‌های بزرگ، خانواده‌های کوچک، مجردها و دانشجویان. در این راستا، اطلاعات سفارش‌های قبلی (شامل اندازه سفارش، قیمت، تعداد دفعات خرید و دیگر موارد) به فرد داده و از او خواسته می‌شود هر مشتری را در یکی از دسته‌های بیان شده قرار دهد. این مثالی از «یادگیری نظارت نشده» (Unsupervised Learning) است، زیرا طی آن پیش‌بینی انجام نمی‌شود، بلکه صرفا مشتریان در گروه‌های گوناگون قرار می‌گیرند. «خوشه‌بندی» (Clustering) یکی از پرکاربردترین اشکال یادگیری نظارت شده است. در این مطلب، دو مورد از پر کاربردترین اشکال خوشه‌بندی یعنی روش «K-میانگین» (K-Means) و خوشه‌بندی «سلسله مراتبی» (Hierarchical) معرفی می‌شوند.

الگوریتم خوشه‌بندی K-Means

در ادامه، نگاهی به نحوه عملکرد الگوریتم خوشه‌بندی انداخته خواهد شد. تابع make_blobs در کتابخانه پایتون «سایکیت‌لِرن» (Scikit learn) قرار دارد. با استفاده از این تابع، چهار خوشه تصادفی برای کمک به کار خوشه‌بندی ساخته می‌شود.

# import statements
from sklearn.datasets import make_blobs
import numpy as np
import matplotlib.pyplot as plt
# create blobs
data = make_blobs(n_samples=200, n_features=2, centers=4, cluster_std=1.6, random_state=50)
# create np array for data points
points = data[0]
# create scatter plot
plt.scatter(data[0][:,0], data[0][:,1], c=data[1], cmap=’viridis’)
plt.xlim(-15,15)
plt.ylim(-15,15)

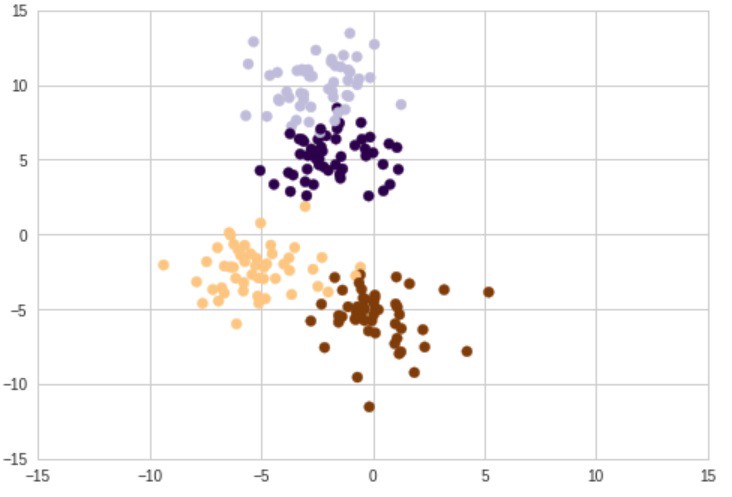
خروجی کد را می‌توان در نمودار زیر به خوبی مشاهده کرد.

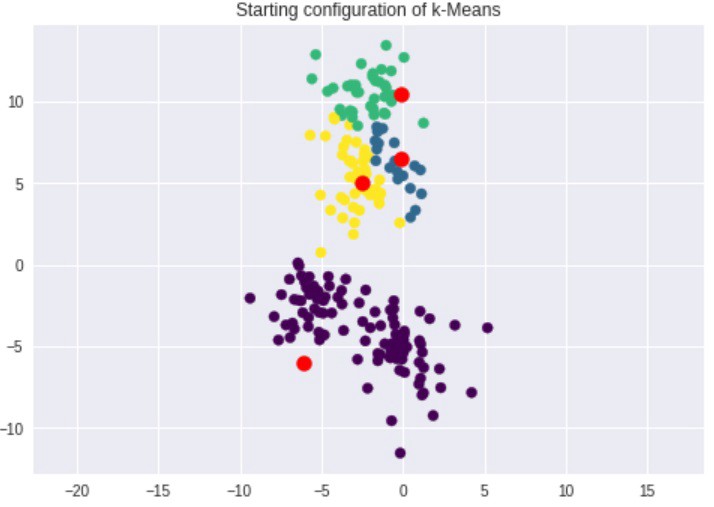
همانطور که مشهود است، چهار خوشه وجود دارد که با چهار رنگ مختلف مشخص شده‌اند. اما هم‌پوشانی‌هایی بین دو خوشه بالایی و همچنین، بین دو خوشه پایینی وجود دارد. اولین گام در خوشه‌بندی k-means انتخاب «مرکزوارها» (centroids) است. از آنجا که در این مثال K=4 است (از پیش بیان شده که مشتریان در چهار دسته قرار بگیرند)، نیاز به چهار مرکزوار تصادفی است. در ادامه پیاده‌سازی کد مربوط به این کار از پایه، ارائه شده است.

در ادامه، هر نقطه دریافت و نزدیک‌ترین مرکزوار به آن پیدا می‌شود. روش‌های گوناگونی برای محاسبه فاصله وجود دارد، ولی در اینجا از «فاصله اقلیدسی» (Euclidean Distance) استفاده شده که با استفاده از np.linalg.norm در پایتون قابل انجام است. 

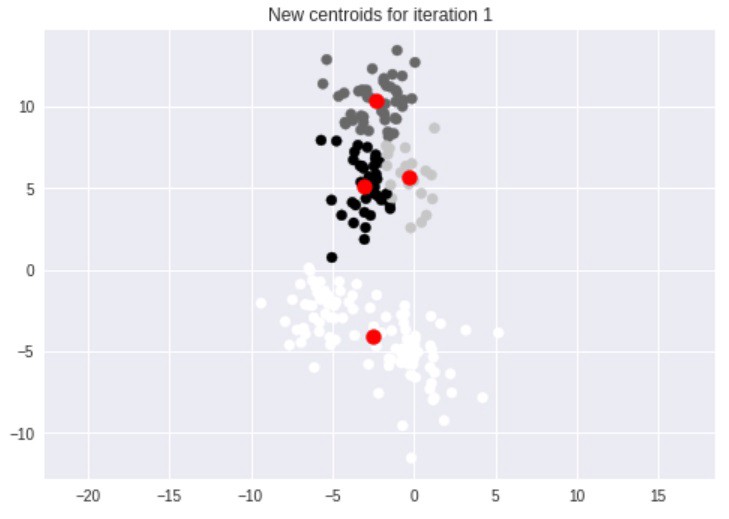
اکنون که چهار خوشه وجود دارد، مرکزوارهای جدید برای خوشه‌ها پیدا می‌شوند.

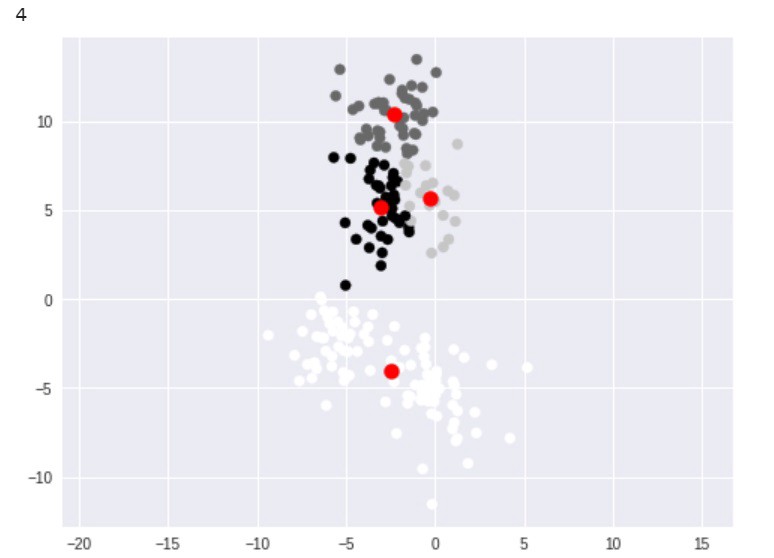
سپس، هر نقطه مجددا با نزدیک‌ترین مرکزوار تطابق داده می‌شود و این فرآیند تا هنگامی که دیگر نتوان خوشه‌ها را بهبود داد تکرار می‌شود. در این مطلب، هنگامی که پردازش پایان پذیرفت، نتیجه زیر حاصل می‌شود.

شایان توجه است که این خوشه‌ها اندکی با خوشه‌های اصلی متفاوت هستند. این خوشه‌ها حاصل تله مقداردهی اولیه تصادفی هستند. اساسا، مرکزوارهای تصادفی می‌توانند موقعیت چهار خوشه در خوشه‌بندی K-Means را مشخص کنند. این نتیجه مورد نظر نیست. اما یک راهکار برای غلبه بر چالش موجود، استفاده از الگوریتم ++k-means است، که بذر بهتری را برای پیدا کردن بهترین خوشه‌ها می‌پاشد. خوشبختانه، این مورد به طور خودکار در پیاده‌سازی k-means که در پایتون مورد استفاده قرار می‌گیرد انجام شده است.

پیاده‌سازی خوشه‌بندی k-means

برای اجرا k-means در پایتون، نیاز به «وارد کردن» (Import) کلاس KMeans از کتابخانه Scikit Learn است.

# import KMeans
from sklearn.cluster import KMeans

شایان توجه است که در اسناد،  ++k-means، پیش‌فرض است. بنابراین، نیاز به انجام تغییر برای اجرای این روش بهبودیافته نیست. اکنون، k-means روی blob‌ها (که در یک آرایه «نام‌پای» (NumPy) با نام «points» قرار گرفته‌اند) اجرا می‌شود.

# create kmeans object
kmeans = KMeans(n_clusters=4)
# fit kmeans object to data
kmeans.fit(points)
# print location of clusters learned by kmeans object
print(kmeans.cluster_centers_)
# save new clusters for chart
y_km = kmeans.fit_predict(points)

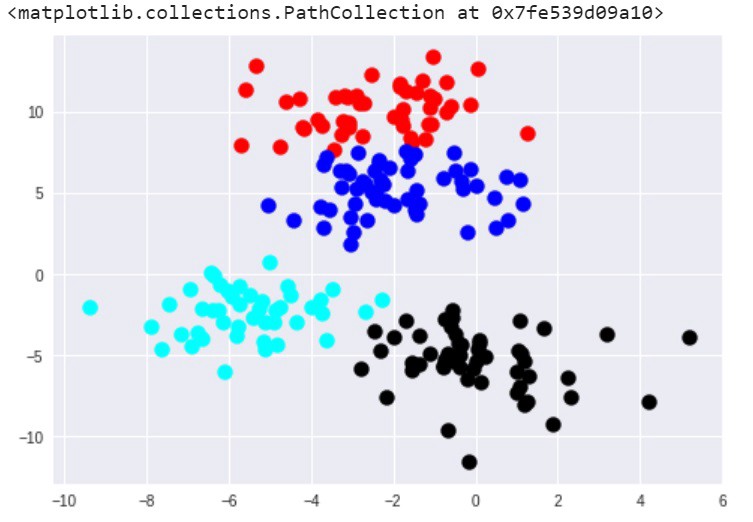
اکنون، می‌توان با اجرای کد زیر در matplotlib نتایج را مشاهده کرد.

plt.scatter(points[y_km ==0,0], points[y_km == 0,1], s=100, c=’red’)
plt.scatter(points[y_km ==1,0], points[y_km == 1,1], s=100, c=’black’)
plt.scatter(points[y_km ==2,0], points[y_km == 2,1], s=100, c=’blue’)
plt.scatter(points[y_km ==3,0], points[y_km == 3,1], s=100, c=’cyan’)

اکنون چهار خوشه وجود دارد. شایان توجه است که الگوریتم ++k-means نسبت به روش k-means اصلی عملکرد بهتری دارد. زیرا این روش، به خوبی مرزهای خوشه‌های اولیه ساخته شده را ثبت و نگهداری می‌کند.

روش k-means به دلیل سرعت و سادگی، یکی از پرکاربردترین روش‌های خوشه‌بندی است. دیگر راه متداول خوشه‌بندی، خوشه‌بندی سلسله مراتبی است.

پیاده‌سازی خوشه‌بندی سلسله‌مراتبی تجمعی

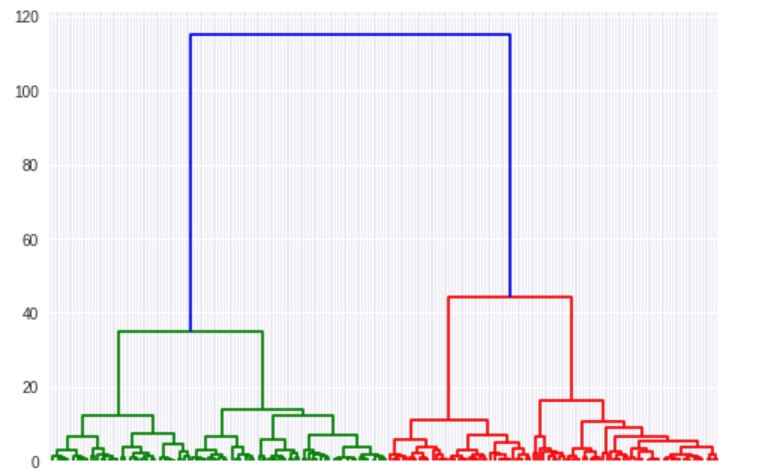
راهکار کلیدی مورد استفاده برای انجام خوشه‌بندی در «خوشه‌بندی سلسله مراتبی تجمعی» (Agglomerative hierarchical clustering) با k-means اساسا متفاوت است. در خوشه‌بندی سلسله‌مراتبی، به جای انتخاب تعداد خوشه‌ها و آغاز با مرکزوارهای تصادفی، کار بدین صورت آغاز می‌شود که هر نقطه در مجموعه داده یک خوشه است. سپس، دو نقطه نزدیک‌تر بهم پیدا و با یکدیگر در یک خوشه ادغام می‌شوند. پس از آن، دو نقطه نزدیک به هم بعدی یافت و با هم در یک خوشه قرار می‌گیرند. این فرآیند تا هنگامی انجام می‌شود که تنها یک خوشه بسیار بزرگ باقی بماند. در طول فرآیند بیان شده، چیزی ساخته می‌شود که به آن «دندروگرام» (Dendrogram) گفته می‌شود. این نمودار، تاریخچه آنچه طی ساخت خوشه‌ها برای نقاط داده به وقوع پیوسته است را نمایش می دهد. 

دندروگرام، هر خوشه و فاصله آن‌ها را ترسیم می‌کند. می‌توان از نمودار دندروگرام برای پیدا کردن خوشه‌ها برای هر عددی که کاربر انتخاب کند استفاده کرد. در دندروگرام بالا، به سادگی می‌توان نقاط اولیه برای اولین خوشه (نقاط آبی)، دومین خوشه (قرمز) و سومین خوشه (سبز) را مشاهده کرد. تنها سه خوشه اول با بهره‌گیری از رنگ‌ها رمزگذاری شده‌اند، اما اگر به کل دندروگرام در ناحیه قرمز نگاه شود، می‌توان نقطه آغازین چهارمین خوشه را مشاهده کرد. دندروگرام تا هنگامی اجرا می‌شود که هر نقطه داده در خوشه اختصاصی خودش قرار داشته باشد.  در ادامه، پیاده‌سازی الگوریتم خوشه‌بندی سلسله مراتبی تجمعی در پایتون انجام شده است. اکنون، می‌توان کتابخانه‌های لازم را از  scipy.cluster.hierarchy و sklearn.clustering وارد کرد.

# import hierarchical clustering libraries
import scipy.cluster.hierarchy as sch
from sklearn.cluster import AgglomerativeClustering

اکنون، دندروگرام ساخته می‌شود (که پیش از این در بالا نشان داده شده است). این نمودار، نشان می‌دهد که چه تعداد خوشه مورد نیاز است و نقاط داده از آن خوشه‌ها ذخیره می‌شوند تا نمودار آ‌ن‌ها ترسیم شود.

# create dendrogram
dendrogram = sch.dendrogram(sch.linkage(points, method=’ward’))
# create clusters
hc = AgglomerativeClustering(n_clusters=4, affinity = ‘euclidean’, linkage = ‘ward’)
# save clusters for chart
y_hc = hc.fit_predict(points)

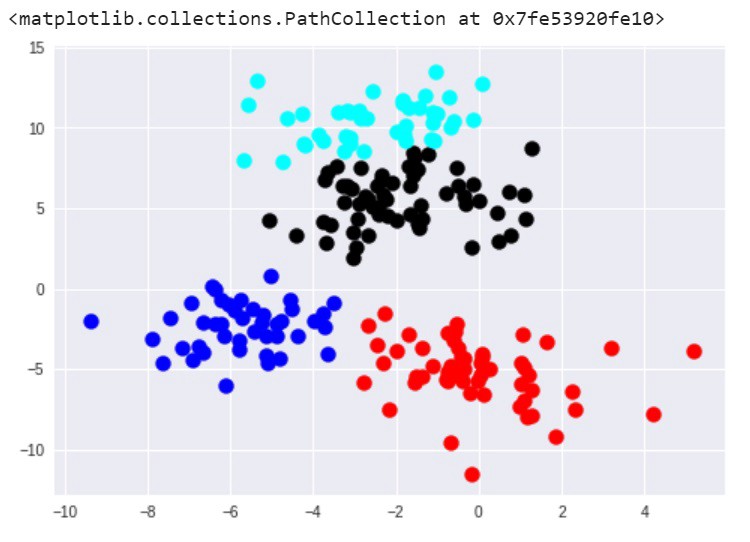
اکنون، کاری مشابه آنچه در الگوریتم K-Means وجود دارد صورت می‌گیرد و می‌توان خوشه‌ها را با استفاده از matplotlib مشاهده کرد. در ادامه، نتایج این مورد قابل مشاهده هستند.

در این مثال، نتایج الگوریتم‌های K-Means و خوشه‌بندی سلسله‌مراتبی بسیار شبیه به یکدیگر هستند. البته این موضوع همیشه اتفاق نمی‌افتد. اگرچه، به طور کلی، مزیت خوشه‌بندی سلسله‌مراتبی تجمعی آن است که در تلاش برای تولید نتایج دقیق‌تر است. اما از معایب این روش آن است که پیاده‌سازی آن پیچیده‌تر محسوب می‌شود و به زمان/منابع بیشتری نسبت به k-means نیاز دارد.

اگر نوشته بالا برای شما مفید بوده، آموزش‌های زیر نیز به شما پیشنهاد می‌شود:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های یادگیری ماشین و بازشناسی الگو
• مجموعه آموزش‌های شبکه‌های عصبی مصنوعی
• مجموعه آموزش‌های هوش محاسباتی
• مجموعه آموزش‌های برنامه نویسی پایتون (Python)
• آموزش برنامه‌نویسی R و نرم‌افزار R Studio
• مجموعه آموزش‌های برنامه نویسی متلب (MATLAB)

 

منبع [+]