مروری کلی بر مفاهیم طراحی الگوریتم
طراحی الگوریتم
در اینجا مروری کلی بر مفاهیم طراحی الگوریتم در ۹ بخش خواهیم داشت.

طراحی الگوریتم
در اینجا مروری کلی بر مفاهیم طراحی الگوریتم در ۹ بخش خواهیم داشت.
بخش اول:
پیچیدگی الگوریتم ها و مرتبه توابع
مرتب سازی درجی
مرتب سازی درجی (Insertion Sort) یک الگوریتم مرتب سازی ساده بر مبنای مقایسه است. این الگوریتم برای تعداد داده های زیاد کارآمد نیست و در این موارد، الگوریتم های بهتری مثل: مرتب سازی سریع، مرتب سازی ادغامی وجود دارد. مرتب سازی درجی، الگوریتم کارآمدی برای مرتب سازی تعداد کمی از عناصر است که به روشی عمل می کند که بیش تر مردم دسته ای از کارت ها را مرتب سازی می کنند. برای مرتب سازی کارت ها با دست چپ خالی شروع می کنیم و کارت ها روی میزی قرار دارند، سپس هر بار یک کارت را از روی میز بر می داریم و آن را در جای مناسبی در دست چپ قرار می دهیم. برای یافتن جای کارت، آن را با هر یک از کارت هایی که فعلا در دست چپ قرار دارند از چپ به راست مقایسه می کنیم. کارت هایی که در دست چپ قرار دارند همیشه مرتب هستند و این کارت ها ابتدا به صورت دسته ای نامرتب روی میز بوده اند.
نمونه رو به رو طریق عملکرد آن را روی {۳, ۷, ۴, ۹, ۵, ۲, ۶, ۱} نشان میدهد :

پیچیدگی الگوریتم
زمانی که رویه Insertion Sort صرف می کند به اندازه ورودی بستگی دارد. مرتب سازی هزار عدد، زمان بیش تری از مرتب سازی ده عدد مصرف می کند و همچنین Insertion Sort بسته به این که اعداد ورودی چقدر مرتب باشند برای دو دنباله به طول های برابر، زمان متفاوتی را مصرف می کند.
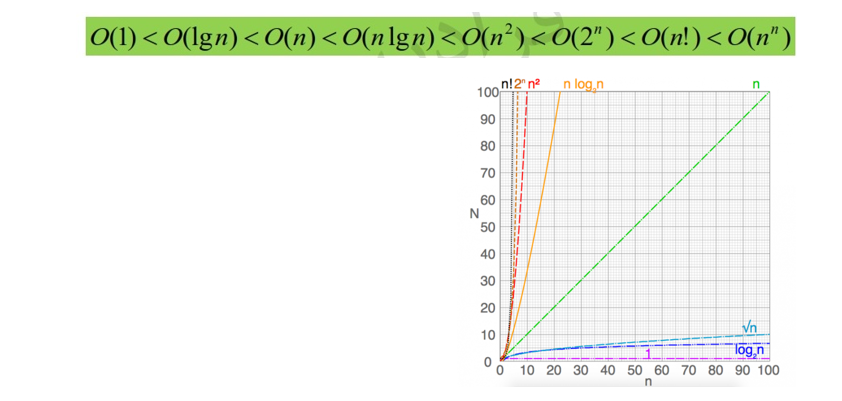
مقایسه مرتبه های اجرایی:
مساله برج هانوی
برج هانوی یک مساله معروف الگوریتمی است که پیشینه تاریخی بسیار طولانی دارد.
اولین بار این مساله در یک معبد شکل گرفت، سه برج الماس در این معبد وجود داشت که در اولین برج، ۶۴ حلقه از کوچک به بزرگ مرتب شده بودند. کاینان قصد داشتند تا این حلقه ها را از روی این برج، به برج دیگر منتقل کنند و معتقد بودند با انجام این کار، عمر دنیا به پایان خواهد رسید.
شرح مساله بدین صورت است: سه میله داریم که در اولین میله n مهره قرار دارد، میخواهیم این مهرهها را به سومین میله منتقل کنیم با این شرط که در هر مرحله و در هر میله، مهره های موجود در آن میله از بالا به پایین به ترتیب کوچک به بزرگ باشند.
بخش دوم:
مرتبه روابط بازگشتی
روابطی که در تعریفشان از خودشان استفاده می شود، روابط بازگشتی نام دارند. مثلا فیبوناچی یک رابطه بازگشتی می باشد. بسیاری از الگوریتم ها نیز به صورت بازگشتی مساله را حل می کنند و از این رو، تحلیل زمانی الگوریتم هایی که زمان اجرای آن ها بر اساس یک تابع بازگشتی مشخص می شود اهمیت پیدا می کند. الگوریتم هایی مانند: مرتب سازی ادغامی از این دسته الگوریتم ها می باشند. برای این کار دو روش متداول وجود دارد.
قضیه اصلی:

بخش سوم:
روش تقسیم و حل
یکی از روش های حل مسائل الگوریتم، این روش می باشد. روش مورد نظر ما بدین صورت عمل می کند که ابتدا مساله اصلی را به چند زیر مساله تقسیم می کند، سپس زیر مساله های ایجاد شده را، حل می کند و پس از آن، با ادغام کردن این زیر مساله ها با یک دیگر، سوال را برای حالت کلی حل می کند. یکی از معروف ترین سوال هایی که با این روش حل می شود، مرتب سازی است.
مرتب سازی ادغامی
مرتب سازی ادغامی نوعی مرتب سازی مقایسه ای از مرتبه زمانی (O (nlogn) O (nlogn می باشد که یک نمونه از روش تقسیم و حل می باشد و در بیش تر پیاده سازی ها پایدار بوده و ترتیب ورودی های مساوی را در خروجی حفظ می کند.
الگوریتم
ایده الگوریتم این است که با تقسیم مساله به دو زیر مساله کوچک تر از مرتب بودن دو لیست کوچک تر برای به دست آوردن لیست حاصل از ادغام آن ها استفاده می کند. می توان الگوریتم مرتب سازی ادغامی را در چند مرحله به صورت کلی بررسی کرد:
- اگر اندازه لیست ۰ یا ۱ بود آن لیست به صورت مرتب شده است در غیر این صورت، آن را به دو لیست که اندازه آن ها یا با هم برابر است یا ۱ واحد فرق دارد تقسیم می کنیم.
- به صورت بازگشتی هر یک از دو لیست را مرتب می کنیم.
- دو لیست مرتب شده را با هم ادغام می کنیم و لیست را مرتب می کنیم.
- برای ادغام ۲ تا اشاره گر برای اول هر دو لیست می گیریم و در هر مرحله اعداد متناظر ۲ اشاره گر را با هم مقایسه می کنیم و هر کدام را که کوچک تر بود را در یک آرایه دیگر می نویسیم و اشاره گر متناظر آن را یک واحد جلو می بریم.
- در آخر هم اشاره گری که به پایان زیر لیست خود نرسیده را تا آخر زیر لیست آن جلو می بریم و اعداد متنظر آن را در آرایه کمکی می ریزیم.
- در آخر هم اعداد آرایه کمکی را در آرایه اصلی کپی می کنیم (ادغام ۲ لیست به اندازه های a و b از O(a+b) O(a+b) می باشد چون دو اشاره گر در مجموع a+b گام جلو می آیند).
ابتدا روند الگوریتم را توسط یک نمونه نشان می دهیم آرایه ۵،۲،۴،۷،۱،۳،۲،۶ را در نظر بگیرید ابتدا این آرایه را نصف می کنیم، پس دو آرایه به طول ۴ به دست می آید، که برابر است با (۵،۲،۴،۷) و (۱،۳،۲،۶) سپس این روال را تا جایی ادامه می دهیم که طول آرایه ها برابر یک شود، که برابر است با (۶) (۲) (۳) (۱) (۷) (۴) (۲) (۵) حال به صورت زیر، آن ها را با هم ادغام می کنیم تا به آرایه اصلی مان برسیم.

پیچیدگی الگوریتم
در مرتب کردن n تا عنصر مرتب سازی ادغام در حالت میانگین و بدترین حالت دارای زمان اجرای (θ (nlogn) θ (nlogn می باشد. اگر زمان اجرای مرتب سازی ادغام برای یک لیست به طول باشد بنابراین، رابطه بازگشتی از تعریف الگوریتم پیروی می کند. در این الگوریتم هر دفعه لیست را به دو زیر لیست تقسیم می کنیم و در هر مرحله n تا گام برای ادغام کردن لازم می باشد.
بخش چهارم:
روش پویا
در این روش همانند روش تقسیم و حل، مساله اصلی را با ترکیب کردن جواب زیر مساله ها حل می کنیم، اما تفاوت این دو روش در این است که در روش تقسیم و حل، مساله را به تعدادی زیر مساله مستقل از یکدیگر تقسیم کرده، هر کدام را جداگانه حل می کنیم و در پایان، جواب ها را با یکدیگر ترکیب می کنیم. در صورتی که در برنامه ریزی پویا مساله ها نباید کاملا مستقل باشند، یعنی خود زیر مساله ها، زیر مساله (یا زیر زیر مساله) های مشترک دارند. این زیر مساله های مشترک با این که از مسیرهای جداگانه ای حاصل شده اند، اما جواب ها در هر دو حالت یکسان است و نیازی به محاسبه دوباره آن ها نیست، به همین دلیل در برنامه ریزی پویا جواب این زیر مساله ها را در یک جدول (یا هر ساختار دیگری) نگه داری می کنیم و اگر دوباره به آن نیاز پیدا کردیم، به راحتی جواب را از جدول می خوانیم و نیازی به محاسبه دوباره آن نیست. این تفاوت شاید بسیار ساده و ناچیز به نظر برسد اما در عمل، با همین راهکار ساده، زمان حل مسائل به طور چشم گیری کاهش پیدا می کند.
در کل، حل مساله به روش پویا، شباهت بسیاری به حل مسائل به صورت استقرایی دارد، چون همانند استقرا در برنامه نویسی پویا، مساله به مسائل کوچکتر اما مشابه مساله اصلی تقسیم می شود و جواب مساله اصلی با فرض دانستن جواب این مسائل اصلی به دست می آید و در انتها هم باید به مرحله ای برسیم که جوابش را به سادگی بتوانیم محاسبه کنیم (همانند پایه استقرا) همچنین برای اثبات درستی آن معمولا از استقرا استفاده می شود (البته معمولا در برنامه نویسی پویا اگر روش حل درست انتخاب شده باشد، روش اثبات آن واضح است)
برای مثال دنباله فیبوناچی را در نظر بگیرید، برای محاسبه جمله ششم آن به جمله پنجم و چهارم نیاز است، همچنین برای محاسبه جمله پنجم نیز به جمله چهارم احتیاج داریم. شاید برای همین مثال دو بار حساب کردن یک جمله آن قدرها هم مشکلی نباشد، چون حداکثر باید هر مقدار را دو بار حساب کنیم، نه؟ اما مشکل این است که در هر کدام از این محاسبه ها باید جمله سوم و دوم را هم دوباره محاسبه کنیم و برای محاسبه جمله سوم هم باید دوباره مقدار جمله دوم را حساب کنیم، پس تا همین الان جمله دوم را چهار بار حساب کرده ایم و اگر این کار را باز هم ادامه دهیم تعداد محاسبه ها رشد نمایی خواهد داشت.
به جای این کار می توانیم هر موقع که جوابی را پیدا کردیم، مقدارش را در جایی (مثل یک جدول) ذخیره کنیم و هر موقع که خواستیم مقداری را محاسبه کنیم، ابتدا چک کنیم که آیا مقدارش در جدول وجود دارد یا نه. اگر بود که نیازی به محاسبه دوباره نیست، اما اگر نبود آن را محاسبه کرده و یادداشت می کنیم. به این روش، روش به خاطرسپاری یا (Memoization) می گویند. این روش به اصطلاح از بالا به پایین است، چون ابتدا سعی می کنیم مساله های بزرگ تر (بالاتر) را حل کنیم و اگر احتیاج شد به مراحل پایینتر (کوچک تر) می رویم.
اما یک راه سرراست تر هم وجود دارد. تمام اعضای دنباله را از ابتدا محاسبه و در یک آرایه ذخیره کنیم تا به مقدار دلخواه مان برسیم، چون تمام مقدارهای قبلی را داریم، محاسبه هر کدام از اعضای دنباله فقط احتیاج به یک جمع ساده دارد. این روش را به اصطلاح پایین به بالا میگویند چون در مقایسه با روش به خاطر سپاری، ابتدا مقدارهای کوچک تر محاسبه می شوند، سپس مقدارهای بزرگ تر و در انتها جواب اصلی سوال.
مساله خرد کردن پول
فرض کنید کسی می خواهد یک مقدار خاص پول از یک دستگاه خودپرداز برداشت کند. این دستگاه خودپرداز n نوع اسکناس مختلف دارد و از هر کدام به هر مقدار که بخواهد در اختیار دارد. این دستگاه می خواهد بداند آیا می تواند با استفاده از این اسکناس ها آن مقدار خاص از پول را به فرد تقاضا کننده بدهد یا نه. تمام مقادیر اعداد طبیعی اند. اگر می تواند، از کدام اسکناس ها و به چه مقدار؟
جواب مساله بستگی به خواص اسکناس هایی دارد که در اختیار داریم. مثلا اگر اسکناس واحد داشته باشیم، می توانیم تمام مقادیر را پرداخت کنیم یا اگر تمام اسکناس ها به یک عدد خاص مثلا پنج بخش پذیر باشند، نمی توان مقادیری که به آن عدد بخش پذیر نیستند را پرداخت یا در حالت های خاص جواب را با فرمولی ریاضی سادهای به دست آورد اما در حالت کلی کار سخت تر می شود.
این سوال راه حلی کارآمدتر و پیچیده تر از روشی که در این جا آمده، دارد که از روش برنامه ریزی پویا استفاده نمی کند. در قسمت مسائل نمونه، صورت سوال این مدل پیچیده تر آمده است.
بخش پنجم
روش حریصانه
معمولا در سوال هایی که با روش برنامه ریزی پویا حل می شوند، امکان دارد اولین ایده حل سوال، استفاده از روش حریصانه باشد. در بسیاری از موارد می توان با روش حریصانه، به نزدیکی جواب اصلی رسید، یا حتی روش هایی که ثابت شده، مثلا حداکثر جوابی نصف بهترین جواب تولید می کنند، اما در حالت کلی، اکثر این روش ها مثال نقضی دارند و حتی یک مثال نقض برای اثبات اشتباه بودن یک راه کافی است، پس همیشه یادتان باشد که روش حریصانه همیشه غلط است، مگر این که اثباتی داشته باشد.
البته این حرف به این معنا نیست که روش حریصانه به درد نمی خورد و همیشه جواب اشتباه می دهد، بلکه یعنی تا وقتی که تا حد خوبی به درستی راه حلتان مطمئن نباشید، بهتر است که از این روش استفاده نکنید، چون برای هر سوال تعداد خیلی زیادی روش حریصانه وجود دارد که اشتباه اند و رد کردن آن ها معمولا کار ساده ای نیست و وقت زیادی می گیرد.
مساله کوله پشتی (حریصانه)
این مساله شکل های متنوع ای دارد، یکی از فرم های آن در کوله پشتی پویا بررسی شده است. در حالت کلی این مساله به صورت زیر تعریف می شود:
فرض کنید یک کوله پشتی با حجمی ثابت و مجموعه ای از اشیاء دارید که هر کدام از آن ها حجمی و ارزشی دارند. می خواهید کوله پشتی خود را به نحوی پر کنید که حجم اشیا برداشته شده از حجم کوله پشتی بیشتر نباشد و مجموع ارزش اشیا بیشینه باشد.
در بعضی از شکل های مساله تعداد یک شی بیشمار و در بعضی محدود است، در بعضی از اشکال اشیا ارزشی برابر دارند و در بعضی اشیا می توانند به صورت پیوسته برداشته شوند (۲٫۵ کیلوگرم شن یا بنزین در یک مخزن (کولهپشتی)).
لازم به ذکر است که در بیشتر این شکل ها الگوریتم حریصانه جواب بهینه را نمی دهد.
الگوریتم
از کوله پشتی خالی شروع کرده و در هر مرحله، کوله پشتی را با شی ای که بیشترین ارزش را نسبت به حجم دارد پر می کنیم تا وقتی که کوله پشتی پرشود یا آن شی تمام شود.
پیچیدگی الگوریتم
در صورت مرتب بودن اشیا ، پیچیدگی الگوریتم از O (n) است، در غیر این صورت از O (nlgn) می باشد.
بخش ششم:
روش عقب گرد
یک الگوریتم عمومی برای یافت جواب های مسائل محاسباتی است. این روش با ترتیبی از قبل معلوم شروع به ساخت کاندید هایی برای جواب مساله کرده و پس از فهمیدن این که یک کاندید ناتمام توانایی کامل شدن به یک راه حل کامل را ندارد، آن را ترک می کند . مساله ۸ و زیر یک مساله معروف برای این روش است.
روش پس گرد ابزار مناسبی برای حل کردن مسائل برآورده سازی شرایط مساله، مانند مسائل سودوکو، جدول کلمات متقاطع و… است.
این روش مجموعه کاندید های ناتمام که در عمل، قابلیت کامل شدن به جواب هایی از مساله را دارند را پیمایش می کند. معمولا این پیمایش به صورت کامل کردن جواب به ترتیب صعودی قسمت اضافه شده انجام می شود.
به صورت انتزاعی می توان مجموعه کاندید ها را به صورت راس های یک درخت نشان داد، به صورتی که هر کاندید ناتمام پدر راسی هایی است که با یک مرحله کامل تر کردن کاندید به آن ها می توان رسید. در نتیجه برگ های درخت نمایان گر کاندیدهایی هستند که دیگر قابلیت گسترش را ندارند. الگوریتم کلی این روش به صورت زیر است:
الگوریتم با شروع از ریشه درخت به ترتیب عمق اول درخت بالا را می پیماید و در هر مرحله ۳۳ عمل زیر را انجام می دهد:
۱) درصورتی که کاندید CC قابلیت کامل شدن به جوابی از مساله را نداشته باشد، از جستجوی کل زیر درخت CC صرف نظر می شود ( به عبارت دیگر شاخهی cc را هرس میکند).
۲) در صورتی که CC جوابی از مساله باشد آن را گزارش می کند.
۳) به صورت بازگشتی زیر درخت های CC را پیمایش می کند.
پیچیدگی الگوریتم
الگوریتم های پس گرد معمولا پیچیدگی نمایی دارند.
فروشنده دوره گرد
فرض کنید n شهر و طول مسیر های بین آن ها به شما داده شده است، کمترین مسافتی که باید طی شود که با شروع از یک شهر همه شهر ها دقیقا یک بار دیده شوند و دوباره به همان شهر اولیه برگردیم چه قدر است؟
پیچیدگی الگوریتم
زمان اجرای این الگوریتم O (n!) است.
بخش هفتم:
الگوریتم های گراف
۱) الگوریتم های پیمایش گراف (Graph)
در این پیمایش گراف را از راس گفته شده شروع می کنیم و همه رئوس مجاور آن را ملاقات می کنیم، سپس این عمل را با راس ملاقات شده بعدی انجام می دهیم. BFS از یک صف استفاده می کند، ابتدا راس شروع (s) را در صف Q قرار می دهد و سپس در یک حلقه while عنصر سر صف را بر می دارد ملاقات می کند و همه رئوس مجاور آن را به صف اضافه می کند تا زمانی که صف، خالی شود
پیمایش عمقی گراف (Depth-first search)
در این روش، پیمایش گراف را از یک راس شروع می کنیم و یکی از رئوس مجاورش را ملاقات می کنیم، حال این عمل را با راس جدید انجام می دهیم. واضح است که نتیجه DFS نیز منحصر به فرد نیست.
الگوریتم کراسکال (kruskal)
الگوریتم کراسکال، یک الگوریتم حریصانه پیمایش گراف است که در آن یال ها به ترتیب صعودی وزنشان مرتب می شوند، سپس به ترتیب، یال ها بررسی می شوند و اگر سیکل تشکیل نشود (اگر یال Safe باشد) انتخاب می شود در غیر این صورت از آن یال صرف نظر (Reject) می شود.
در این الگوریتم، یال ها را بر اساس وزن به صورت صعودی مرتب می کنیم، سپس از اولین یال شروع می کنیم و هر یالی که با یال هایی که قبلا انتخاب کردیم دور نمی سازد را انتخاب می کنیم تا جایی که درخت تشکیل شود، اما چگونه متوجه شویم که یال جدید با یال های انتخابی قبلی دور نمی سازد؟ کافیست گرافی که تاکنون از یال های انتخابی تشکیل شده را به مولفه های همبندی تقسیم کنیم و اگر یال جدید هر دو سر آن در یک مولفه بود، یال جدید دور ایجاد می کند و در غیر این صورت اضافه کردن یال جدید مشکلی ندارد.
هر راس متغیری همراه خود دارد که شماره مولفه همبندیش را نشان می دهد. در ابتدا هر راس، خود یک مولفه همبندیست و وقتی یک یال بین دو مولفه ارتباط ایجاد می کند باید شماره مولفه همبندی هر دو گروه یکی شود.
شبه کد
- تمام یال ها را به ترتیب صعودی وزن مرتب کنید.
- برای هر راس v یک مجموعه بسازید.
- یال (u ,v) را انتخاب کنید.
- اگر مجموعه u و v یکی نیستند. کارهای زیر را انجام بدید.
- مجموعه آن ها را ادغام کنید.
- یال (u ,v) را به عنوان یالی از درخت پوشای کمینه بردارید.
- اگر هنوز n-1 یال انتخاب نشده به شماره ۳ بروید.
- پایان
الگوریتم پریم (Prim)
این الگوریتم گراف نیز حریصانه است. روش آن بدین صورت است که از راس گفته شده شروع می کنیم، راسی را ملاقات می کنیم که با راس شروع، مجاور است و وزن یالش مینیمم است. در مرحله بعدی راسی را ملاقات می کنیم که با حداقل یکی از رئوس ملاقات شده مجاور است و وزن یالش مینیمم است، به همین ترتیب در هر مرحله یک راس ملاقات نشده را ملاقات می کنیم.
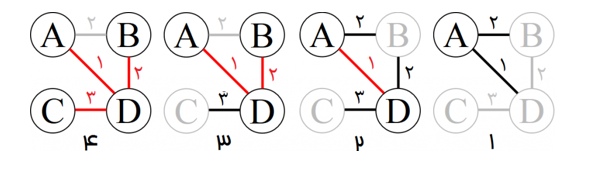
مثال: تصویر زیر نمایشی از اجرای الگوریتم پریم روی یک مثال است.
یال های سیاه، گزینه هایی انتخابی در هر مرحلهاند. یال های قرمز و راس های سیاه انتخاب شدهاند. یال ها و راس های خاکستری انتخاب نشده اند.
بخش هشتم:
الگوریتم های مرتب سازی
مرتب سازی حبابی: یک الگوریتم مرتب سازی ساده است که فهرست را پشت سر هم پیمایش می کند تا هر بار عناصر کنار هم را با هم سنجیده و اگر در جای نادرست بودند جا به جا یشان کند. در این الگوریتم این کار باید تا زمانی که هیچ جا به جایی در فهرست رخ ندهد، ادامه یابد و در آن زمان، فهرست مرتب شده است. این مرتب سازی از آن رو حبابی نامیده می شود که هر عنصر با عنصر کناری خود سنجیده شده است و در صورتی که از آن کوچک تر باشد جای خود را به آن می دهد و این کار همچنان پیش می رود تا کوچک ترین عنصر به پایین فهرست برسد و دیگران نیز به ترتیب در جای خود قرار گیرند (یا به رتبه ای بالاتر روند یا به پایین تر فهرست رانده شوند) این عمل همانند پویش حباب به بالای مایع است.
این مرتب سازی از آن رو که برای کار با عناصر، آن ها را با یکدیگر می سنجد، یک مرتب سازی سنجشی است.
با فرض داشتن n عضو در فهرست، در بدترین حالت n (n – 1) / 2 عمل لازم خواهد بود.
بدترین زمان اجرا و پیچیدگی متوسط مرتب سازی حبابی هر دو (O (n^2 می باشند که در آن n تعداد عناصری است که باید مرتب شوند.
الگوریتم های مرتب سازی بسیاری وجود دارند که بدترین زمان اجرای آن ها از این بهتر است یا پیچیدگی متوسط آن ها (O (nlgn است. حتی بقیه الگوریتم های مرتب سازی از (O (n^2 مثل مرتب سازی درجی، عملکرد بهتری نسبت به مرتب سازی حبابی از خود نشان می دهند.
مثال: یک آرایه از عددهای ۵, ۱, ۴, ۲, ۸ اختیار می کنیم و آن را به ترتیب، صعودی و با استفاده از مرتب سازی حبابی مرتب کنیم. در هر مرحله، عناصری که در حال مقایسه شدن با یکدیگر هستند پر رنگ تر نشان داده شده اند:
گذر اول:
(۱, ۵, ۴, ۲, ۸) <= (۵, ۱, ۴, ۲, ۸)
در اینجا الگوریتم دو عنصر اول را مقایسه، و جابه جا می کند.
(۱, ۴, ۵, ۲, ۸) <= (۱, ۵, ۴, ۲, ۸)
(۱, ۴, ۲, ۵, ۸) <= (۱, ۴, ۵, ۲, ۸)
(۱, ۴, ۲, ۵, ۸) <= (۱, ۴, ۲, ۵, ۸)
حالا آرایه مرتب شده است ولی الگوریتم هنوز نمی داند که این کار، کامل انجام شده است یا نه، که برای فهمیدن، احتیاج به یک گذر کامل بدون هیچ جابه جایی (Swap) داریم:
گذردوم
(۱, ۲, ۴, ۵, ۸) <= (۱, ۲, ۴, ۵, ۸)
(۱, ۲, ۴, ۵, ۸) <= (۱, ۲, ۴, ۵, ۸)
(۱, ۲, ۴, ۵, ۸) <= (۱, ۲, ۴, ۵, ۸)
(۱, ۲, ۴, ۵, ۸) <= (۱, ۲, ۴, ۵, ۸)
در نهایتT آرایه مرتب شده است و الگوریتم می تواند پایان پذیرد.
بخش نهم:
مسائل np ,p
کلاس P
به طور کلی مسائل تصمیم گیری را به چهار کلاس تقسیم می کنیم. مسائلی که برای حل آن ها الگوریتم یا الگوریتم هایی با مرتبه زمانی چند جمله ای یافت شده است، کلاس الگوریتم های معین یا الگوریتم های قطعی را تشکیل می دهند. این کلاس را با علامت ویژه p که کوتاه شده Polynomial می باشد نمایش می دهیم.
الگوریتم هایی که برای کامپیوتر های رایج طراحی می گردند، الگوریتم های معین نامیده می شوند. در این الگوریتم ها نتیجه هر عمل کاملا مشخص، معین و قطعی است. P کلاس کلیه مسائل تصمیم گیری است که برای حل آن ها الگوریتم معین با مرتبه زمانی چند جمله ای وجود دارد.
کلاس NP
برای معرفی کلاس NP باید ماشینی (کامپیوتری) با مشخصات جدید تعریف کنیم. ماشینی را تصور کنید که افزون بر توانایی اجرای دستورهای معین و قطعی قادر است برخی دستورهای نامعین را نیز اجرا کند. یک دستور نامعین، دستوری است که نتیجه اجرای آن از قبل قابل پیش بینی نیست. الگوریتم هایی که برای یک کامپیوتر نامعین طراحی می شوند الگوریتم های نامعین نامیده می شوند.
آیا کلاس p زیر مجموعه کلاس NP است؟
بله هر مساله کلاس P زیر مجموعه کلاس NP هست چون مساله P خودش با پیچیدگی زمانی چند جمله ای قابل حل است پس در صورت داشتن جواب میشود درستی یا نادرست آن را تعیین کرد ( یعنی همون ویژگی کلاس NP ) پس جزو کلاس NP هم هست.
آیا کلاس Np زیر مجموعه کلاس P است؟
این سوال را به این شکل می شود مطرج کرد که آیا می شود برای هر سوال NP الگوریتمی از پیچیدگی زمانی چند جمله ای پیدا کرد؟
در صورت مشخص شدن جواب این سوال میشود تعیین کرد که آیا P=NP است یا نه، ولی هنوز کسی جواب این سوال رو نمی داند و جالب است که بدانید این یکی از مسائل ریاضی حل نشده توی دنیا است که ۱ میلیون دلار جایزه هم دارد.
مجموعه: دستهبندی نشده




 (No Ratings Yet)
(No Ratings Yet)