جمله زیر از «جان فون نویمان» (John von Neumann)، بسیار معروف است:

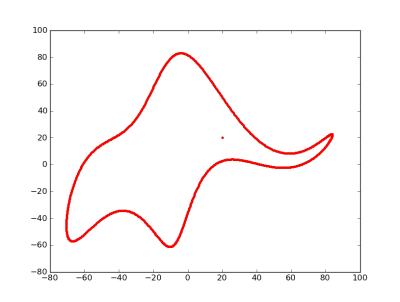
با چهار پارامتر، می‌توانم یک فیل را برازش (Fit) کنم و با پنج پارامتر می‌توانم کاری کنم که خرطومش را تکان دهد.

منظور او از این گفت این است که وقتی یک مدل پیچیده داده‌ها را به خوبی برازش می‌دهد، نباید تعجب کرد. با تعداد کافی از پارامترها، می‌توان هر مجموعه داده‌ای را برازش داد. اما به معنای واقعی کلمه هم می‌توان با چهار پارامتر، یک فیل را برازش داد.

در یک مقاله که توسط «جرگن مایر» (Jürgen Mayer) و همکاران در سال ۲۰۱۰ نوشته شده است [+]، روش برازش یک فیل با استفاده چهار پارامتر پیچیده را ارائه کرده‌اند. با استفاده از کد پایتون زیر، می‌توان یک فیلم را برازش و نمودار آن را ترسیم کرد.

“””
Author: Piotr A. Zolnierczuk (zolnierczukp at ornl dot gov)

Based on a paper by:
Drawing an elephant with four complex parameters
Jurgen Mayer, Khaled Khairy, and Jonathon Howard,
Am. J. Phys. 78, 648 (2010), DOI:10.1119/1.3254017
“””
import numpy as np
import pylab

# elephant parameters
p1, p2, p3, p4 = (50 – 30j, 18 + 8j, 12 – 10j, -14 – 60j )
p5 = 40 + 20j # eyepiece

def fourier(t, C):
f = np.zeros(t.shape)
A, B = C.real, C.imag
for k in range(len(C)):
f = f + A[k]*np.cos(k*t) + B[k]*np.sin(k*t)
return f

def elephant(t, p1, p2, p3, p4, p5):
npar = 6
Cx = np.zeros((npar,), dtype=’complex’)
Cy = np.zeros((npar,), dtype=’complex’)

Cx[1] = p1.real*1j
Cx[2] = p2.real*1j
Cx[3] = p3.real
Cx[5] = p4.real

Cy[1] = p4.imag + p1.imag*1j
Cy[2] = p2.imag*1j
Cy[3] = p3.imag*1j

x = np.append(fourier(t,Cx), [-p5.imag])
y = np.append(fourier(t,Cy), [p5.imag])

return x,y

x, y = elephant(np.linspace(0,2*np.pi,1000), p1, p2, p3, p4, p5)
pylab.plot(y,-x,’.’)
pylab.show()

 

منبع[+]

 

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش اصول و مبانی برنامه‌نویسی
• آموزش برنامه‌نویسی جاوا‎‬
• مجموعه آموزش‌های ریاضیات
• چطور برنامه‌نویس شویم؟ — راهنمای عملی ورود به دنیای برنامه‌نویسی
• زبان برنامه‌نویسی پایتون (Python) — از صفر تا صد