در این مطلب، روش انجام ضرب ماتریس ها با استفاده از الگوریتم استراسن بیان و پیاده‌سازی آن در زبان برنامه‌نویسی C انجام شده است.

ضرب ماتریس ها با استفاده از الگوریتم استراسن

دو ماتریس مربعی A و B با اندازه‌های n x n داده شده است. هدف، پیدا کردن ماتریس حاصل‌ضرب این دو ماتریس است.

روش ساده ضرب ماتریس‌ها

در ادامه، یک راهکار ساده برای ضرب دو ماتریس داده شده است.

void multiply(int A[][N], int B[][N], int C[][N]) 
{ 
    for (int i = 0; i < N; i++) 
    { 
        for (int j = 0; j < N; j++) 
        { 
            C[i][j] = 0; 
            for (int k = 0; k < N; k++) 
            { 
                C[i][j] += A[i][k]*B[k][j]; 
            } 
        } 
    } 
}

پیچیدگی زمانی روش بالا از درجه O(N³)‎ است.

روش تقسیم و حل ضرب ماتریس‌ها

در ادامه، مراحل یک روش تقسیم و حل ساده برای ضرب کردن دو ماتریس مربعی بیان شده است.

• تقسیم ماتریس‌های A و B در ۴ زیر ماتریس با اندازه N/2 x N/2 به صورتی که در تصویر زیر نمایش داده شده است.
• محاسبه مقادیری که در ادامه آمده است، به صورت بازگشتی. 

ae + bg و af + bh و ce + dg و cf + dh

 

در روش بالا، هشت ضرب برای ماتریس‌هایی از اندازه N/2 x N/2 و ۴ جمع انجام شده است. جمع کردن دو ماتریس، زمانی از درجه O(N²)‎ دارد. بنابراین، پیچیدگی زمانی به صورت زیر نوشته می‌شود.

T(N) = 8T(N/2) + O(N²)

با توجه به «قضیه اصلی واکاوی الگوریتم‌ها» (Master’s Theorem) پیچیدگی زمانی الگوریتم بالا از درجه O(N³)‎ و متاسفانه، برابر با روش ساده‌ای است که در ابتدای این مطلب معرفی شد.

الگوریتم استراسن برای ضرب ماتریس‌ها

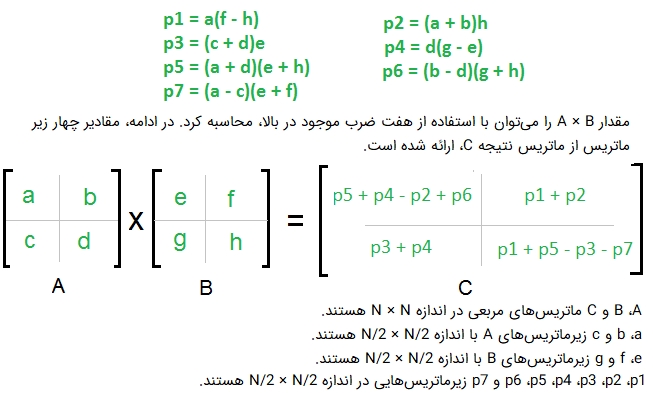
در روش تقسیم و حل ارائه شده در بالا، عامل اصلی که منجر به پیچیدگی زمانی بالایی می‌شود، ۸ فراخوانی بازگشتی است. ایده الگوریتم استراسن، کاهش تعداد فراخوانی‌های بازگشتی به ۷ تا است. روش استراسن از این جهت مشابه با روش ساده تقسیم و حل ارائه شده در بالا است که ماتریس‌ها را به زیرماتریس‌هایی با ابعاد N/2 x N/2 تقسیم می‌کند. این مورد، در تصویر زیر به خوبی به نمایش داده شده است. اما در الگوریتم استراسن، چهار زیر ماتریس از نتیجه با استفاده از فرمولی که در ادامه آمده است محاسبه می‌شوند.

پیچیدگی زمانی جمع و تفریق دو ماتریس به اندازه O(N²)‎ زمان می‌برد. بنابراین، پیچیدگی زمانی را می‌توان به صورت زیر نوشت.

T(N) = 7T(N/2) + O(N²)

با توجه به قضیه اصلی واکاوی الگوریتم‌ها، پیچیدگی زمانی الگوریتم بالا از درجه O(N^Log7)‎ و تقریبا برابر با O(N^2.8074)‎ است. عموما، از الگوریتم استراسن به دلایلی که در ادامه بیان شده است، در کاربردهای جهان واقعی استفاده نمی‌شود.

• ثابت‌های استفاده شده در روش استراسن زیاد هستند و برای کاربردهای معمول، روش ساده، عملکرد بهتری دارد.
• برای «ماتریس‌های خلوت» (Sparse Matrix | ماتریس اسپارس)، روش‌های بهتری وجود دارد که ویژه این نوع ماتریس‌ها ساخته شده‌اند.
• زیرماتریس‌ها در بازگشت، فضای اضافی می‌گیرند.

به دلیل دقت محدود محاسبات کامپیوتری روی مقادیر غیر صحیح، در الگوریتم ساده نسبت به روش استراسن خطاهای بزرگ‌تر کمتری وجود خواهند داشت.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌ نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• رنگ‌آمیزی گراف به روش حریصانه — به زبان ساده
• الگوریتم دایجسترا (Dijkstra) — از صفر تا صد
• الگوریتم پریم — به زبان ساده
• متن کاوی (Text Mining) — به زبان ساده

منبع [+]