مسئله فروشنده دوره گرد — به زبان ساده
مسائل حوزه برنامهنویسی از جهت سادگی و سختی و قابل حل بودن یا نبودن، انواع گوناگونی دارند. یکی از این انواع، مسائل «انپی سخت» (NP-hardness) هستند. مسئله فروشنده دورهگرد (Travelling Salesman Problem) نیز یکی از این نوع مسائل است. در این مطلب، مسأله انپی-سخت فروشنده دورهگرد مورد بررسی قرار میگیرد.
مسئله فروشنده دوره گرد
یک شهر و فاصله بین هر جفت از شهرهای آن داده شده است. مسئله پیداه کردن کوتاهترین مسیر ممکن برای بازدید از همه شهرها دقیقا یکبار و بدون آن است که یک شهر دوبار دیده شود و در نهایت، باید به شهر محل شروع بازگشت. باید به تفاوت بین دور همیلتونی و مسئله فروشنده دورهگرد توجه داشت. دور همیلتونی راهی برای پیدا کردن آن است که آیا توری وجود دارد که هر شهر را دقیقا یکبار ملاقات کند. در مثال زیر، تورهمیلتونی وجود دارد زیرا که گراف کامل است و در حقیقت، حالات گوناگونی از این تور موچود است. در مسئله فروشنده دورهگرد، موضوع پیدا کردن کوتاهترین تور است.
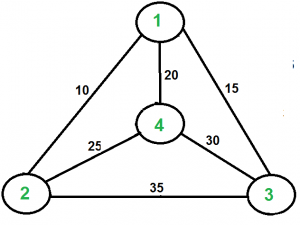
برای مثال، گرافی که در بالا نمایش داده شده مفروض است. تور مسئله فروشنده دورهگرد ۱-۳-۴-۲-۱ است. هزینه این تور برابر با ۱۵+۳۰+۲۵+۱۰ است که برابر میشود با ۸۰. مسئله فروشنده دورهگرد از نوع NP-سخت است؛ یعنی هیچراهکاری از درجه چندجملهای برای حل این مسئله وجود ندارد. در ادامه، راهکارهای گوناگون موجود برای مسأله فروشنده دورهگرد مورد بررسی قرار گرفته است.
راهکار ساده
- فرض میشود شهر ۱ نقطه شروع و پایان است.
- همه !(n-1) جایگشت شهرها تولید میشود.
- هزینه هر جایگشت محاسبه و به دنبال کمترین هزینه جایگشت گشته میشود.
- جایگشت با کمترین هزینه بازگردانده میشود.
پیچیدگی زمانی این روش ساده برای حل مسئله فروشنده دورهگرد از درجه Θ(n!) است.
برنامهنویسی پویا
فرض میشود که راسهای داده شده {۱, ۲, ۳, ۴,….n} باشند. فرض میشود که راس ۱ محل شروع و همچنین، نقطه پایانی است. برای هر راس i (به جز راس ۱) هزینه مسیر کمینه با شروع از راس ۱ به عنوان نقطه شروع و پایان و با تنها یکبار ملاقات کردن هر راس، محاسبه میشود. فرض میشود که هزینه این مسیر cost(i) باشد. هزینه چرخه موجود برابر خواهد بود با cost(i) + dist(i, 1) که در آن dist(i, 1) فاصله از i تا ۱ است. در نهایت، کمینه (Minimum) همه مقادیر [cost(i) + dist(i, 1)] بازگردانده میشود. این راهکار، ساده به نظر میرسد. اکنون، پرسشی که مطرح میشود این است که چطور میتوان cost(i) را محاسبه کرد. برای محاسبه cost(i) با استفاده از برنامهریزی خطی، نیاز به داشتن روابط بازگشتی به صورت زیرمسائل است. در اینحا، عبارت C(S, i) تعریف میشود که هزینه کمینه مسیر برای ملاقات کلیه راسها در مجموعه S دقیقا و تنها یکبار با شروع از راس ۱ و با پایان در i است. کار با همه زیرمجموعههای اندازه ۲ آغاز میشود و C(S, i) برای همه زیرمجموعههایی که S در آنها یک زیرمجموعه است محاسبه میشود و سپس، C(S, i) برای همه زیرمجموعههای S از اندازه ۳ و به همین ترتیب محاسبه میشود. شایان توجه است که ۱ باید در هر زیرمجموعه وجود داشته باشد.
برای یک مجموعه با اندازه n، به تعداد n-2 زیرمجموعه مفروض است که هر یک از اندازه n-1 هستند و در همه زیرمجموعهها، nامین مورد وجود ندارد. با استفاده از رابطه بازگشتی بالا، میتوان راهکار مبتنی بر برنامهنویسی پویا را نوشت. حداکثر O(n*2n) زیرمسئله وجود دارد و هر یک از زیرمسائل، زمان خطی برای حل نیاز دارد. کل زمان اجرا برابر با O(n2*2n) است. پیچیدگی زمانی بسیار کمتر از O(n!) است، اما همچنان نمایی است. فضای مورد نیاز نیز نمایی است. بنابراین، این رویکرد برای گرافهایی با تعداد راس کمی بالاتر، ممکن نیست.
اگر این مطلب برای شما مفید بوده است، آموزشها و مطالب زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ساختمان داده و تحلیل و طراحی طراحی الگوریتم ها
- آموزش درس تحلیل و طراحی الگوریتم های به همراه حل مثالهای عملی
- مجموعه آموزشهای دروس علوم و مهندسی کامپیوتر
- درس الگوریتم های پیشرفته | مفاهیم پایه به زبان ساده
- آموزش ساختمان داده — مجموعه مقالات جامع وبلاگ فرادرس
- پیاده سازی الگوریتم های یادگیری ماشین با پایتون و R — به زبان ساده
- معرفی الگوریتمهای مجانبی، حریصانه و برنامه نویسی دینامیک — به زبان ساده
منبع [+]
مجموعه: مهندسی کامپیوتر برچسب ها: Travelling Salesman Problem, پیچیدگی محاسباتی, تحلیل و طراحی الگوریتم, ساختمان داده, طراحی الگوریتم, فروشنده دوره گرد, مسئله فروشنده دوره گرد




 (No Ratings Yet)
(No Ratings Yet)