آشنایی با نرم افزار متلب – بخش دوم
این پست، بخش دوم از ضمیمه ب کتاب واقعیت مجازی و انیمیشن برای کاربران MATLAB و Simulink است که از سوی مولف این کتاب برای انتشار در اختیار متلب سایت قرار گرفته است. برای آشنایی بیشتر با این کتاب و کسب اطلاعات بیشتر، می توانید به این لینک(+) مراجعه نمایید.
توضیح مختصر از پنجره های موجود در صفحه ی اصلی متلب
این پست، بخش دوم از ضمیمه ب کتاب واقعیت مجازی و انیمیشن برای کاربران MATLAB و Simulink است که از سوی مولف این کتاب برای انتشار در اختیار متلب سایت قرار گرفته است. برای آشنایی بیشتر با این کتاب و کسب اطلاعات بیشتر، می توانید به این لینک(+) مراجعه نمایید.
توضیح مختصر از پنجره های موجود در صفحه ی اصلی متلب
این پست، بخش دوم از ضمیمه ب کتاب واقعیت مجازی و انیمیشن برای کاربران MATLAB و Simulink است که از سوی مولف این کتاب برای انتشار در اختیار متلب سایت قرار گرفته است. برای آشنایی بیشتر با این کتاب و کسب اطلاعات بیشتر، می توانید به این لینک(+) مراجعه نمایید.
توضیح مختصر از پنجره های موجود در صفحه ی اصلی متلب
رسم چند plot در یک figure :
Subplot(n,m,x)
که در این جا n تعداد سط ها ، m تعداد ستون ها x شماره ی plot است.
برای title و یا label گذاشتن در اینجا باید بعد از هر plot این کار را انجام بدهیم.
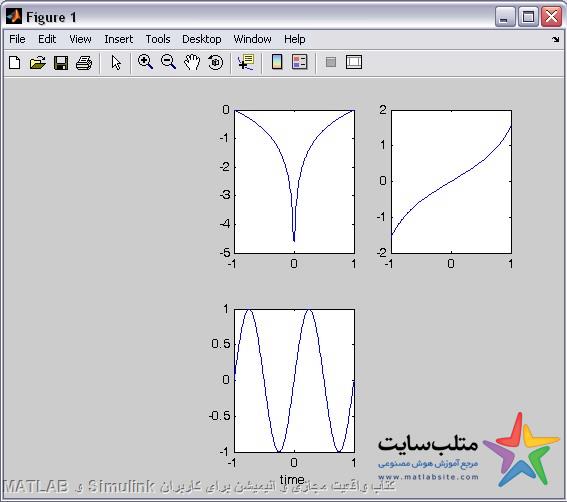
در یک figure 6 قسمتی، در plot پنجم سینوسی و در plot دوم لگاریتمی و در plot سوم tan رسم کنید:
clc
clear all
close all
fs=100;
t=-1:1/fs:1;
y1=sin(2*pi*t);
subplot(2,3,5)
plot(t,y1),xlabel(‘time’)
y2=log(t)
subplot(2,3,2)
plot(t,y2)
y3=tan(t)
subplot(2,3,3)
plot(t,y3)
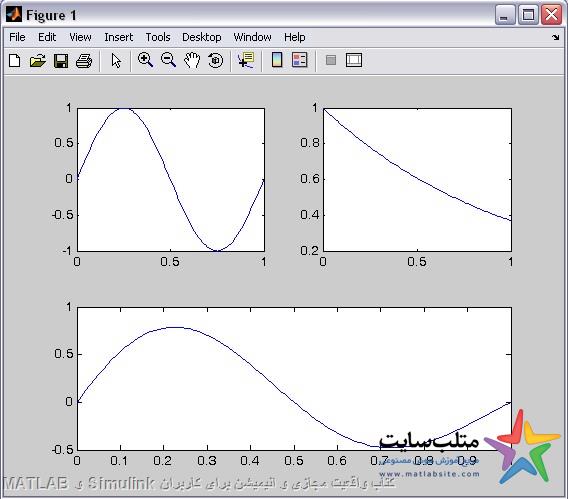
اگر بخواهیم یکی از subplot ها مثلا به اندازه ی ۲ subplot باشد یعنی بزرگتر از subplot های دیگر باشد، از روش زیر استفاده میکنیم.در مثال پایین plot سومی در دو جایگاه سوم و چهارم قرار میگیرد و به اندازه ی دو برابر سایر plot هاست.
clc
clear all
close all
fs=100;
t=0:1/fs:1;
x1=sin(2*pi*t);
x2=exp(-t);
x3=(x1.*x2);
subplot(2,2,1)
plot(t,x1)
subplot(2,2,2)
plot(t,x2)
subplot(2,2,3:4)
plot(t,x3)
نمودار میله ای:
bar(x,f(x))
نمودار گسسته:
Stem(x,f(x))
نمودار پلکانی:
Stairs(x,f(x))
نمودار هیستوگرام:
Hist(f(x),x)
توابع سمبولیک یا آنالوگ:
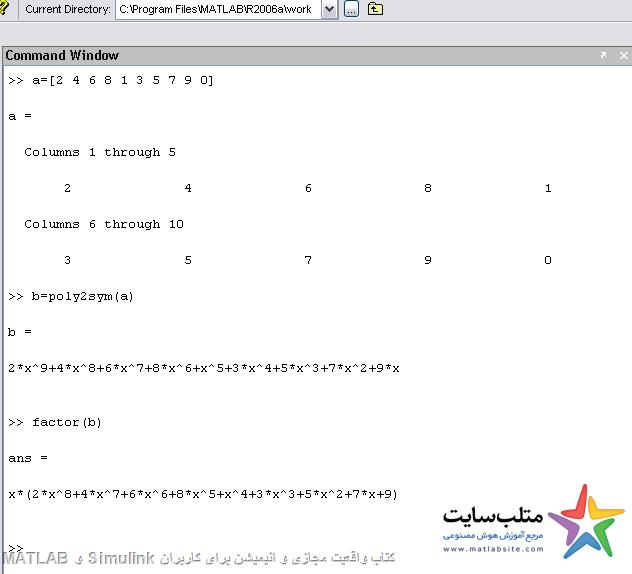
چندجمله ای: polynomial
A=[2 4 6 8] معرف چند جمله ای درجه ۳ است.
A=[an,a(n-1),a(n-2),…,a0]
معرف ضرایب چند جمله ای درجه n است.
X=roots(a) که در آن a یک بردار است، ریشه ها را به ما می دهد.
Poly(x) ضرایب را به ما میدهد.
به طوری که roots و poly برعکس هم عمل میکنند.
هر گاه از poly استفاده کنیم، همیشه ضریب an را ۱ میگیرد و بقیه را تقسیم بر ضریب an میکند تا ضریب an 1 شود.
برای تبدیل polynomial به سمبولیک:
poly2sym()
A=[2 4 6 8]
Poly2sym(a)
Ans=
2*x^3+4*x^2+6*x+8
Syms x بعد از نوشتن این عبارت enter میزنیم و x را به عنوان یک سمبل در نظر میگیرد.
حالا میتوان از این سمبل استفاده کرد و سمبل های دیگر ساخت.
Y=sin(x)
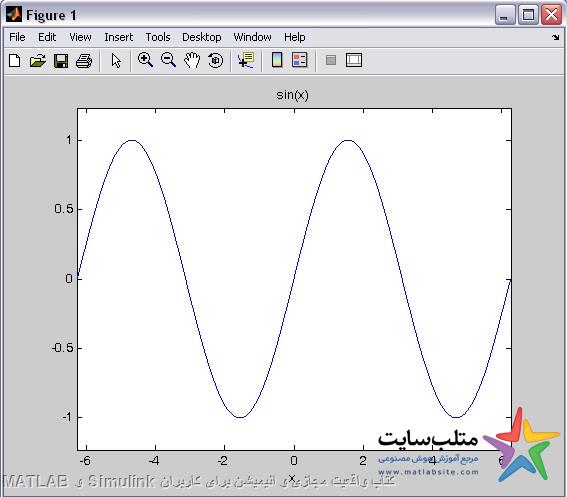
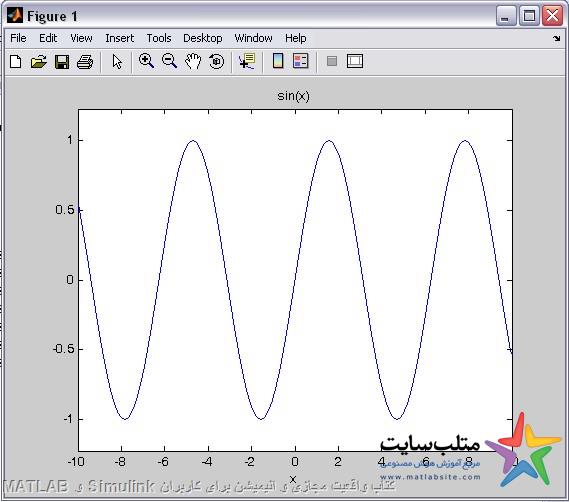
رسم توابع سمبولیک:
Ezplot(y)
که در اینجا y و یا هر عبارت داخل پرانتز باید سمبولیک باشد.
Syms x
Y=sin(x)
Ezplot(y)
به صورت پیش فرض بین -۲pi و ۲pi رسم میکند.
اگر بخواهیم پیش فرضش را تغییر بدهیم:
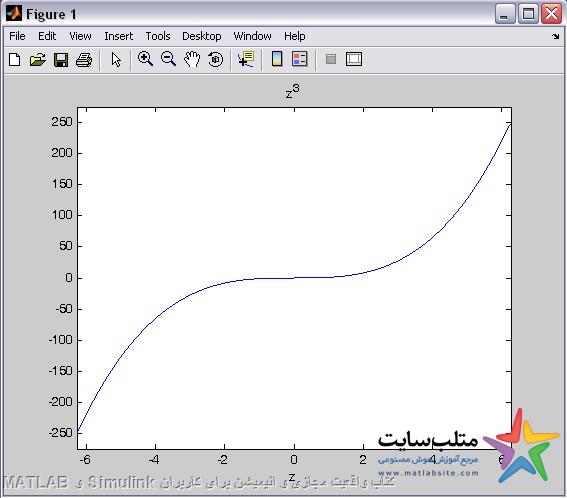
Ezplot(y,[-10,10])
اگر متغیر قبلا سمبولیک نشده باشد میتوانیم داخل ” قرار بدهیم.
Ezplot(‘z^3’)
که در این حالت میتوانیم برای y هم مختصات تعریف بکنیم.
Pretty(a)
به حالت دست نویس نشان میدهد.
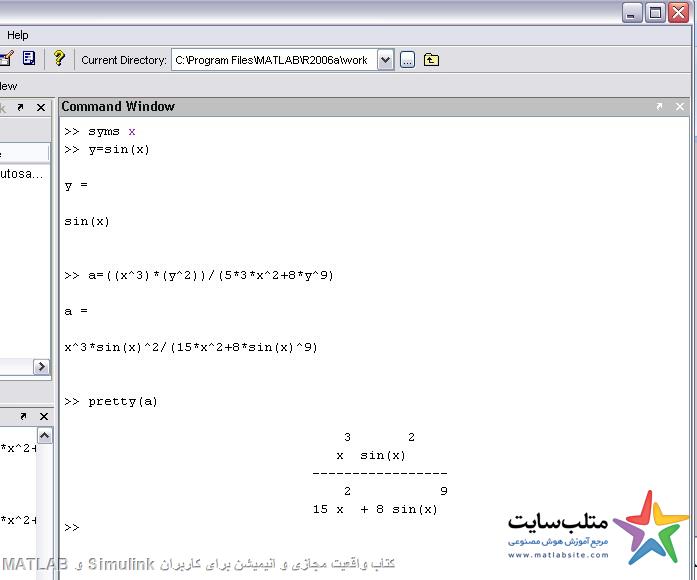
Simple(y)
بسط ها را نشان می دهد.
Factor(a)
اگر سمبلی قابل فاکتور گرفتن باشد از آن فاکتور میگیرد.
Conv(a,b)
که در آن a و b ضرائب چند جمله ای هستند، ضرب convolution انجام می دهد.
Convolution
وقتی به حوزه ی فرکانس برود به ضرب تبدیل میشود. برای فیلتر کاربرد دارد.
Deconv(a,b)
تقسیم است.
مشتق چند جمله ای در بحث چند جمله ای:
Polyder(a)
که در این جا a ضرایب چند جمله ای است.

Polyder(a,b)
مشتق ضرب چند جمله ای است.
[A B]=polyder(a,b)
مشتق تقسیم چند جمله ای است.
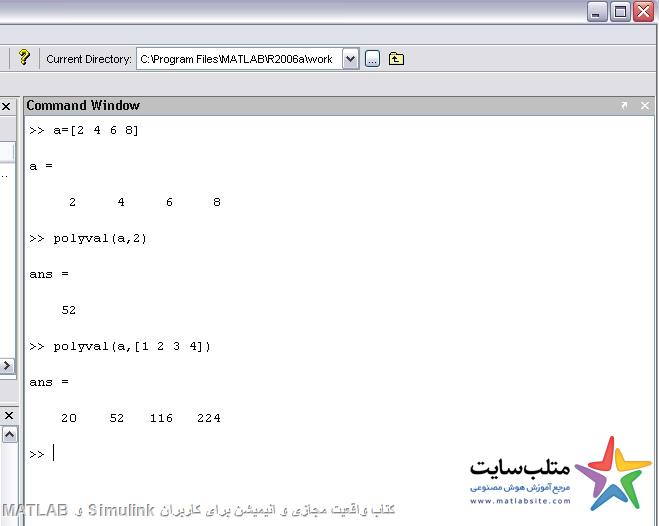
ارزیابی چند جمله ای ها:
Polyval(a,x0)
عدد با بردار x0 را در چند جمله ای a مقدار دهی میکند.
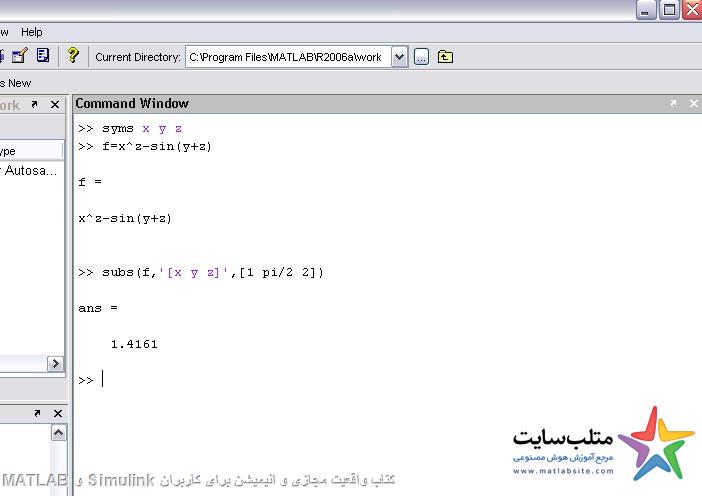
مقدار دهی در حالت سمبولیک:
Subs(f,’x’,a)
عدد a را در تابع f به جای x قرار می دهد.

می توانیم به جای یک متغیر چند مقدار مختلف بگذاریم:
مثلا :
F=x^z-sin(x+z)
Subs(f,'[x y z]’,[1 pi/2 2])
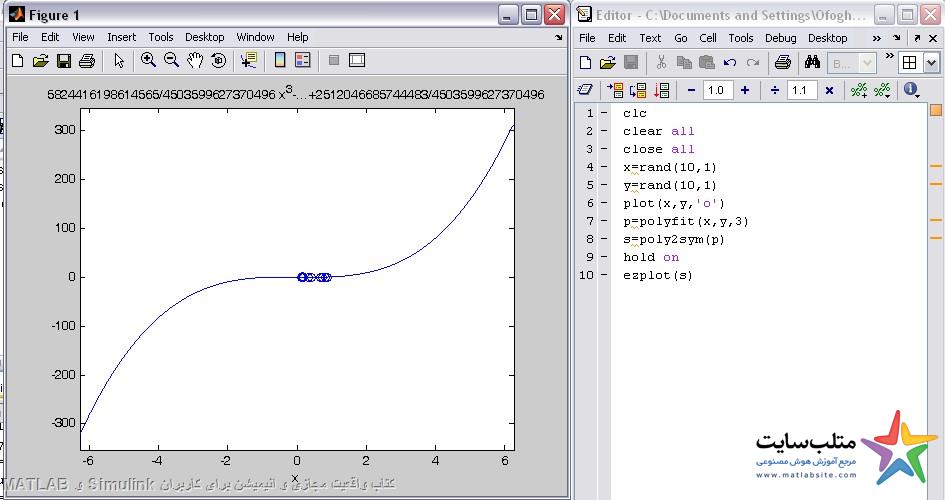
تابع polyfit :
استخراج چند جمله ای درجه n از یک سری نقطه:
polyfit(x,y,n)
درجه ی چند جمله ای باید از تعداد نقاط حداقل یکی کمتر باشد.
حل معادله ی n معادله n مجهول برای حالت سمبولیک:
solve(‘ ‘,’ ‘,’ ‘,…………..)
داخل هر کدام از نماد های ‘ ‘ یک معادله را می نویسیم.
که لازم است قبل از آن تماد مجهول ها را از قبیل a,b,x,…….. سمبولیک کنیم.
مثال:
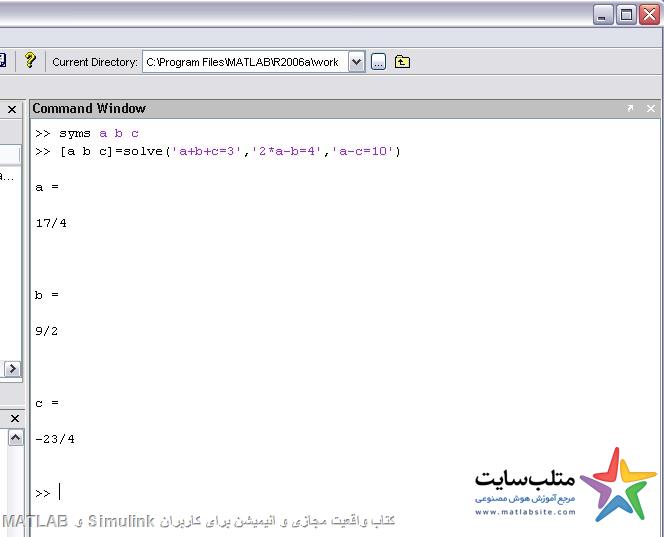
برای حالت غیر سمبولیک:
AX=B
که در این جا A ماتریس ضرائب است وX ماتریس مجهول هاست.
X=A(-1)*B که در اینجا A(-1) همان وارون ماتریس A است.
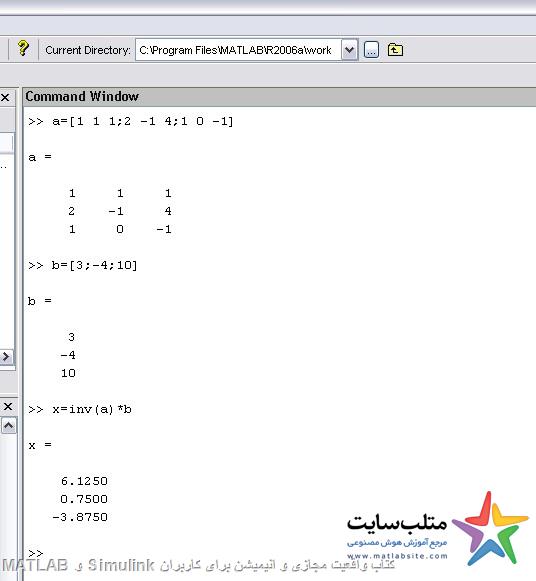
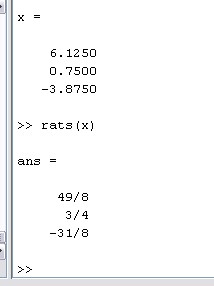
Rats(x)
اعداد را می گیرد و به صورت کسری نمایش می دهد.
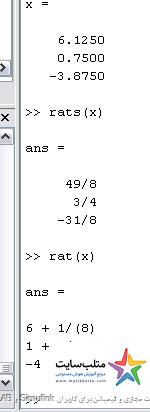
Rat(x) اعداد را می گیرد و به صورت کسرهایی نمایش می دهد که صورت آن ها ۱ است.
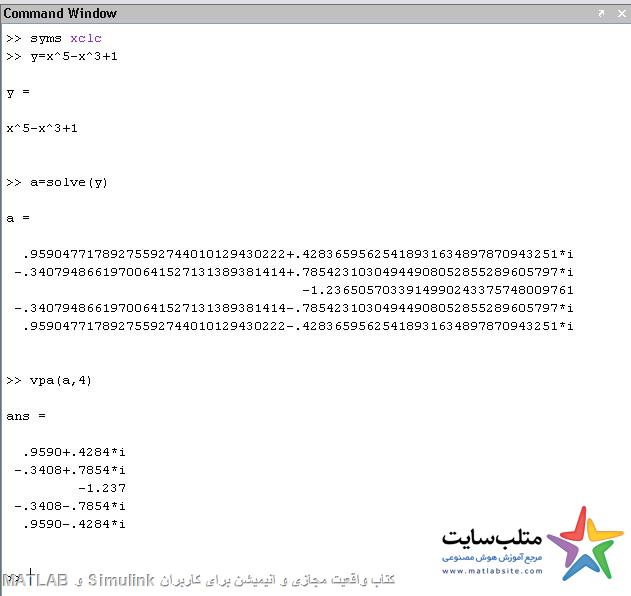
Vpa(a,n) عدد a را تا n رقم نشان می دهد و بقیه را گرد می کند.
حل یک معادله با درجه ی n
Solve(d)
D را برابر صفر می گیرد و معادله را حل می کند.
باید از توابع سمبولیک استفاده کنیم اگر که سمبولیک نبود از نماد ” استفاده می کنیم.
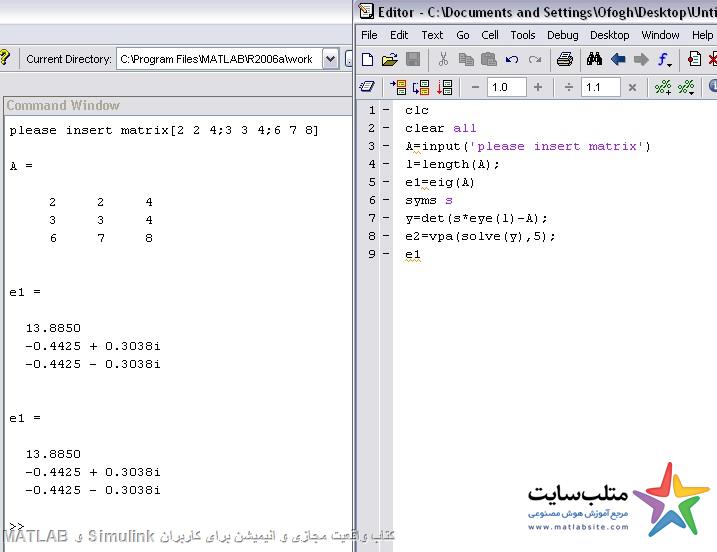
مقادیر ویژه ی ماتریس:
Eig(a)
Det(SI-A)=0
که در آن I ماتریس یکه است.
در درس مدار ۲ در قسمت فضای حالت کاربرد دارد.
اگر
A ماتریس حالت
B ماتریس ورودی
C ماتریس خروجی
D ماتریس انتقال
X متغیر های حالت
U متغیر های ورودی
Y متغیر های خروجی باشند ، مقادیر ویؤه ی ماتریس A فرکانس های طبیعی شبکه هستند.
x.=Ax+Bu
y=Cx+Du
برنامه ای بنویسید که کاربر یک ماتریس مربعی با ابعاد دلخواه وارد کرده و برنامه یک بار مقادیر ویژه را با این تابع و یک بار هم با رابطه ی زیر حساب کند.
Det(SI-A)
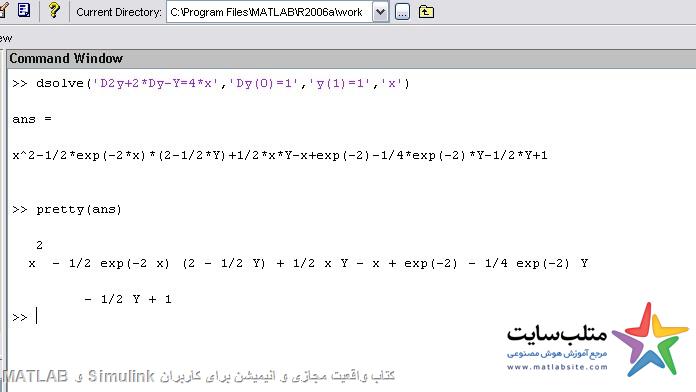
حل معادلات دیفرانسیل در حالت سمبلیک:
Dsolve(‘………’,’…’,’…’,’x’)
که در نماد ” اول باید معادله دیفرانسیل را بنویسیم و در ” های بعدی شرایط اولیه را که باید تعدادشان برابر با درجه ی معادله باشد. و x آخر هم برای این است که معادله بر حسب x است.
برای نشان دادن مشتق باید از D ( حتما D بزرگ ) استفاده کنیم.
به صورت پیش فرض ، متغیر مستقل را t در نظر میگیرد.
مثال:
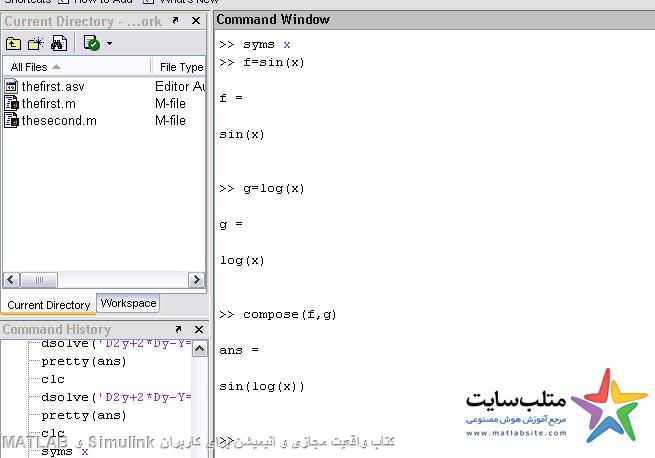
ترکیب توابع سمبولیک:
F(g(x))=fog
Compose(f,g)
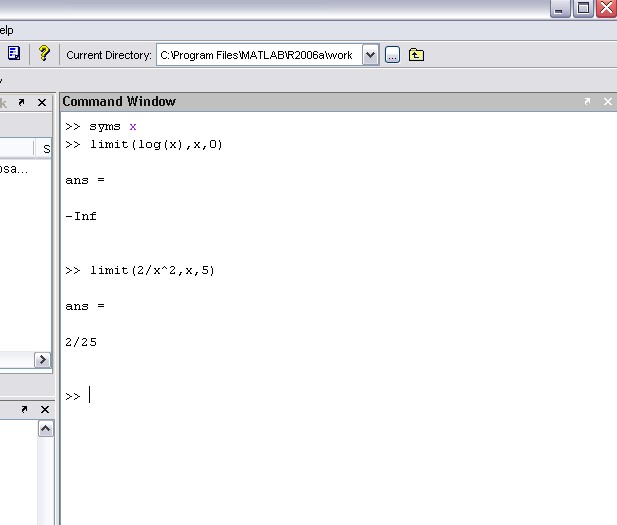
حد توابع سمبولیک:
Limit(f,x,a)
مطالب پیشنهادی
مجموعه: متلب برچسب ها: Matlab, V-Realm Builder, Virtual Reality Toolbox, آشنایی با واقعیت مجازی, جعبه ابزار واقعیت مجازی, جواد پالیزوان زند, کتاب واقعیت مجازی, واقعیت مجازی در متلب




 (No Ratings Yet)
(No Ratings Yet)