این پست، بخش سوم از ضمیمه ب کتاب واقعیت مجازی و انیمیشن برای کاربران MATLAB و Simulink است که از سوی مولف این کتاب برای انتشار در اختیار متلب سایت قرار گرفته است. برای آشنایی بیشتر با این کتاب و کسب اطلاعات بیشتر، می توانید به این لینک(+) مراجعه نمایید.

 

توضیح مختصر از پنجره های موجود در صفحه ی اصلی متلب

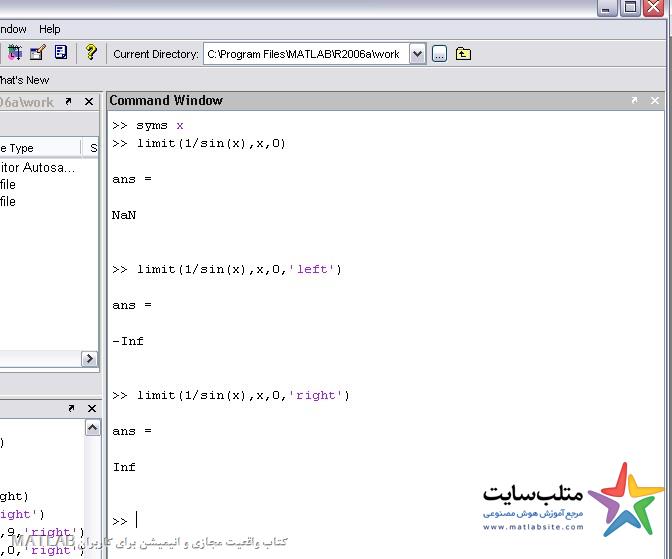
در مواقعی که حد چپ و حد راست با هم برابر نیست ، اگر حد بگیریم NaN  را نمایش می دهد که نشانگر تعریف نشده است . همانطور که در help نرم افزار متلب توضیح داده است NaN مخفف عبارت not a number می باشد.
 اگر بخواهیم حد راست و یا حد چپ گرفته شود باید از right و left استفاده کنیم:

 

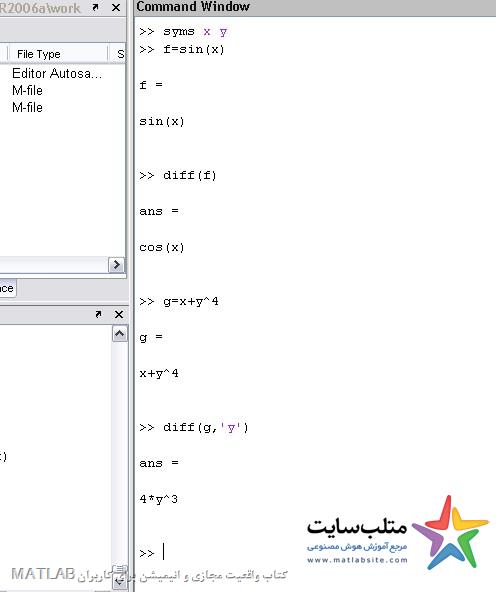
مشتق توابع سمبولیک:

Diff(f)

به صورت پیش فرض ، بر حسب x مشتق می گیرد. ورودی هر چند متغیری که میخواهد داشته باشد مشتق بر حسب x است.
اگر بخواهیم بر حسب متغیر دیگری مشتق بگیرد :

diff(f,’y’)
 

مشتق مرتبه ی n ام:

Diff(f,n)

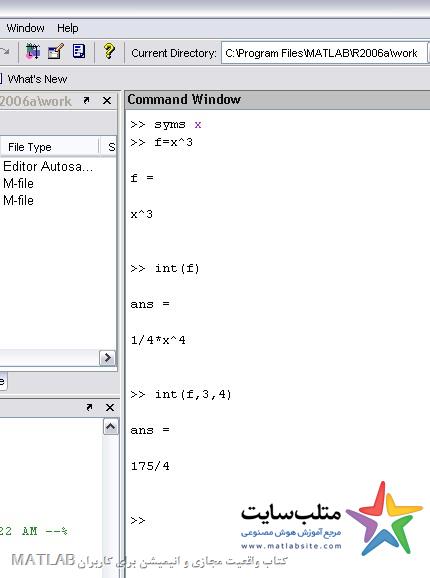
انتگرال عبارات سمبولیک:

Int(f)
Indefinite integral

انتگرال نامعین

Int(f,a,b)    

انتگرال معین
اگر بخواهیم بر حسب متغیر دیگری انتگرال گیری انجام شود :

int(f,y)

برای انتگرال چندگانه میتوانیم ازچند انتگرال داخل هم استفاده کنیم:

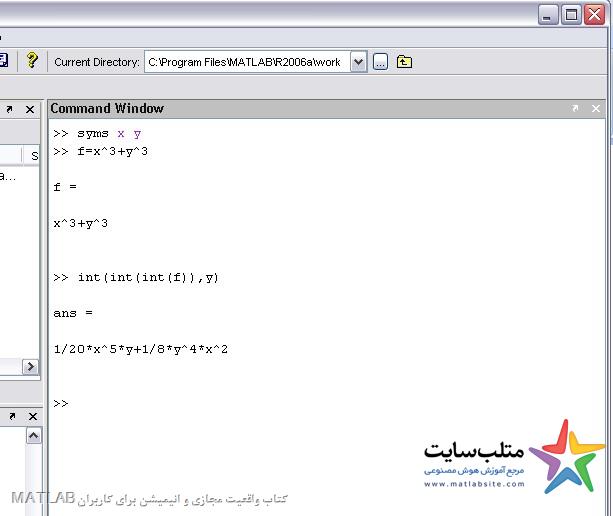
سری تیلور برای توابع سمبولیک:

Taylor(f) 

بسط تیلور حول نقطه ی صفر است.

بسط مک لورن:

taylor(f,m,x0) تا m و حول نقطه ی x0

برنامه ای بنویسید که بسط تیلور تابع sin(x) را حول نقطه ی صفر حساب کند و مشخص کنید تا جمله ی چندم مشتق با شکل خود تابع sin(x) یکی میشود.
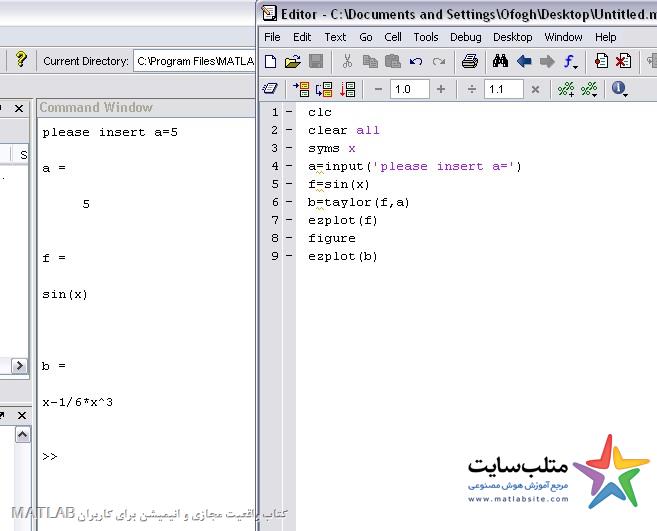
برنامه را به شکلی مینویسیم که کاربر عدد را وارد کند و برنامه بسط تیلور را تا آن عدد محاسبه کند:
مطابق شکل های زیر، عدد a را اول به عنوان مثال از ۵ وارد می کنیم و بعد افزایش میدهیم تا جایی که شکل ها یکی شوند.

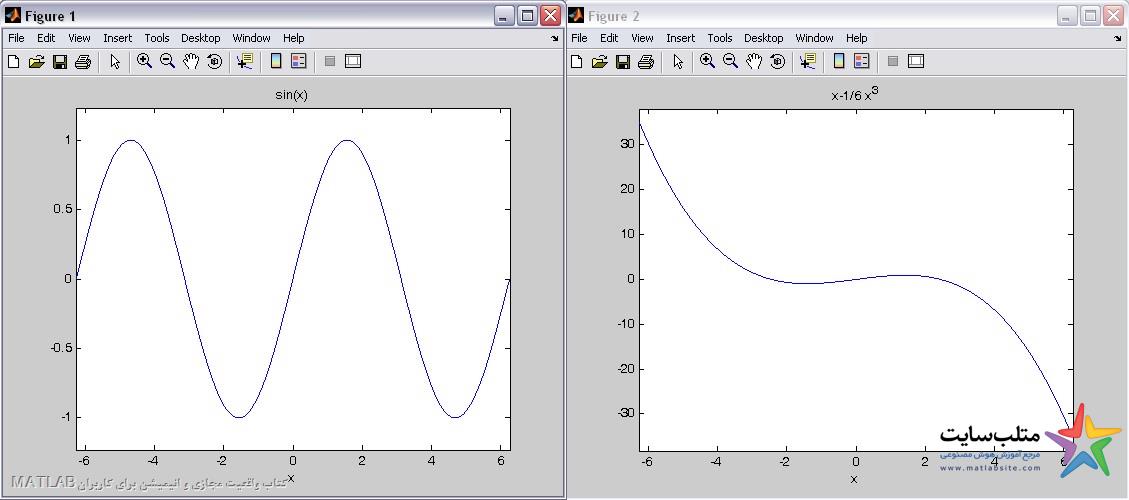
عدد a را برابر با ۱۰ وارد می کنیم: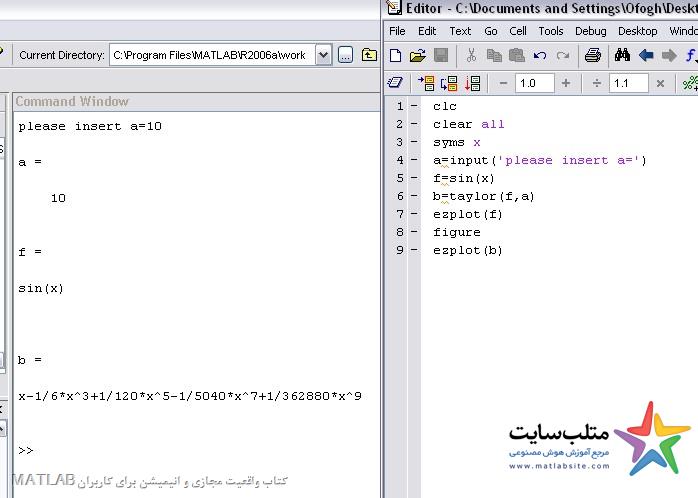

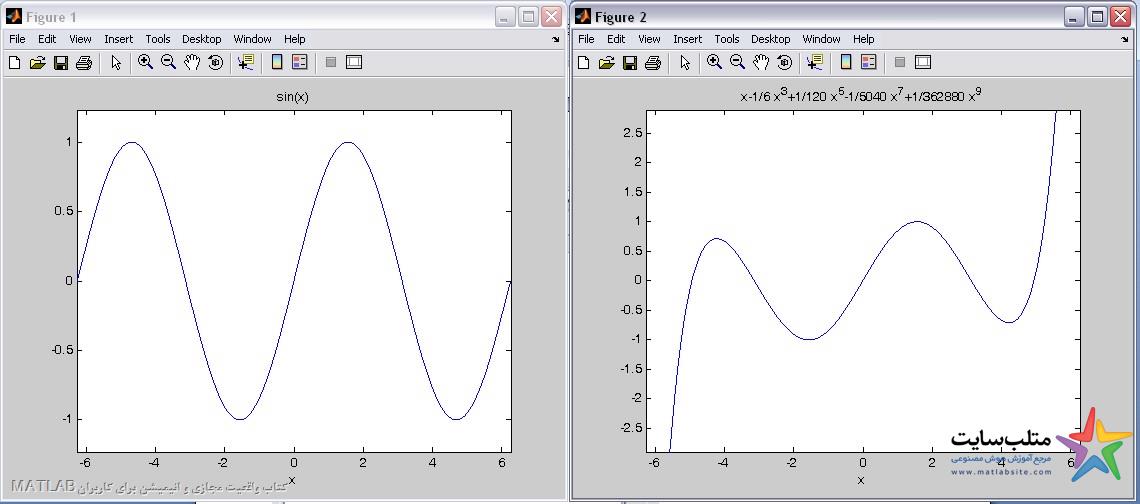
عدد a را ۱۳  وارد می کنیم:

 

 

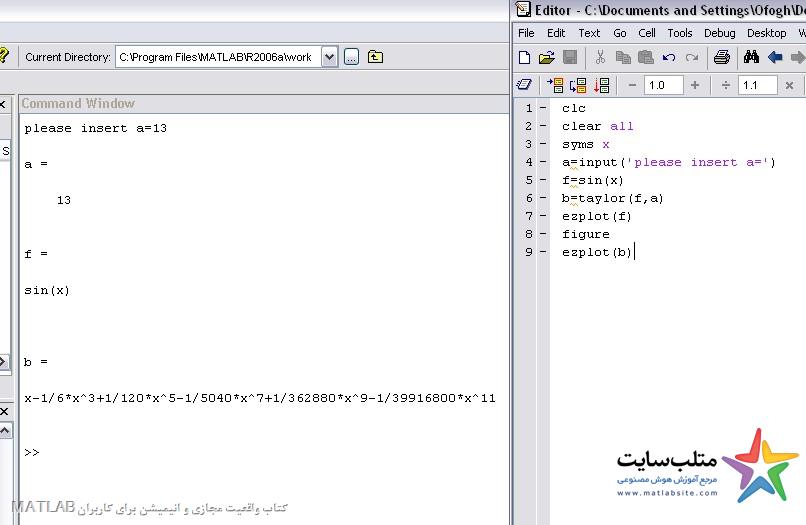
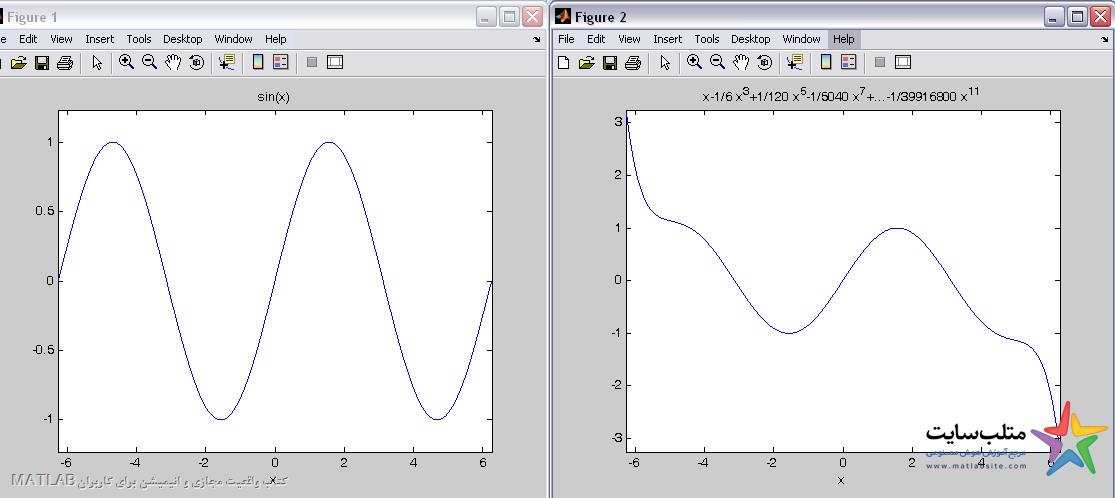
عددa را ۱۴ وارد می کنیم:
 

 

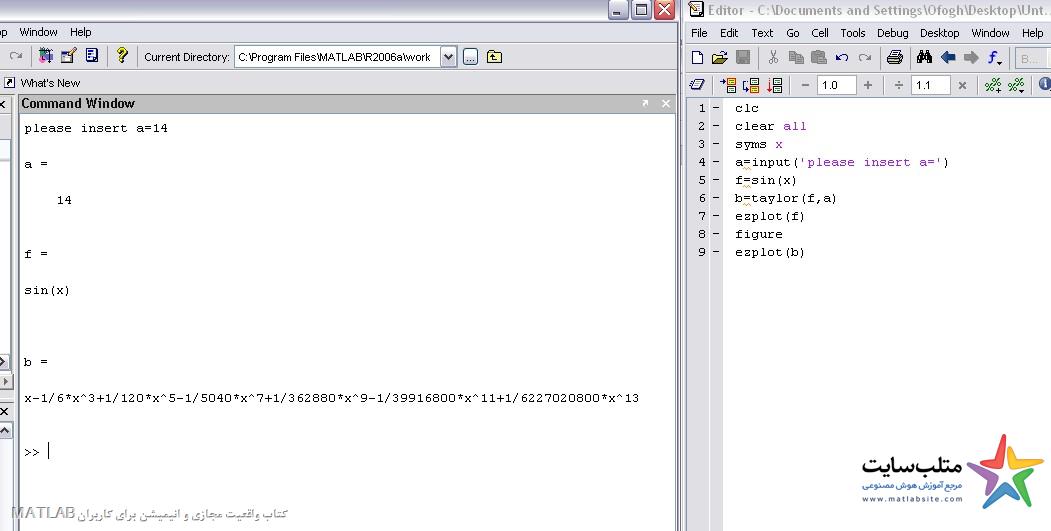
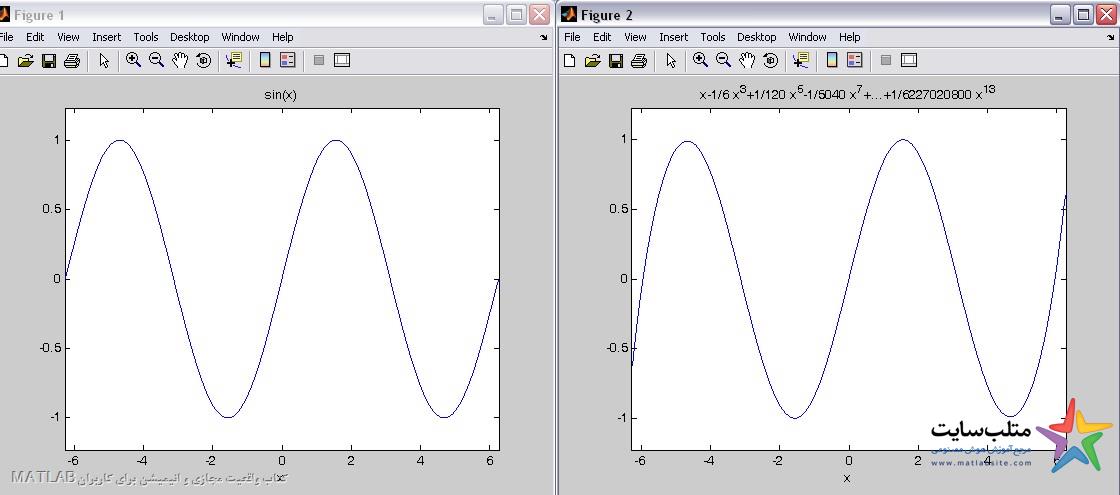
با در نظر گرفتن عدد a برابر با ۱۴ با اندکی خطا دو شکل شبیه هم شدند.

برای اینکه دو شکل را منطبق بر هم ببینیم میتوانیم از hold on استفاده کنیم :

A=14

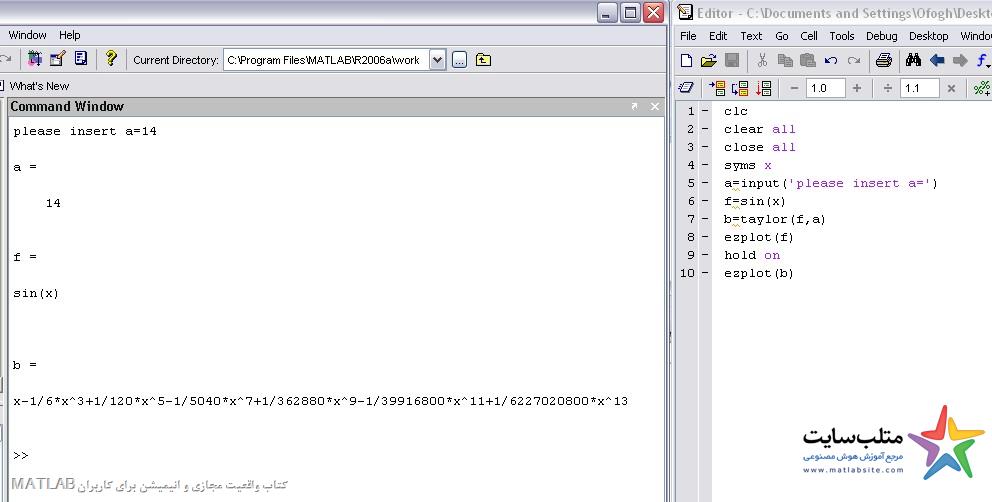
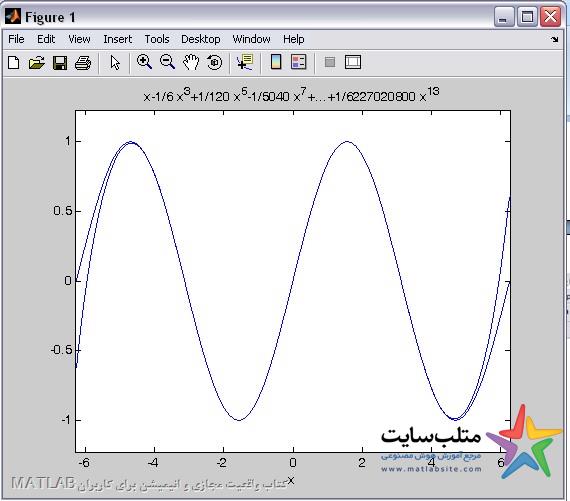
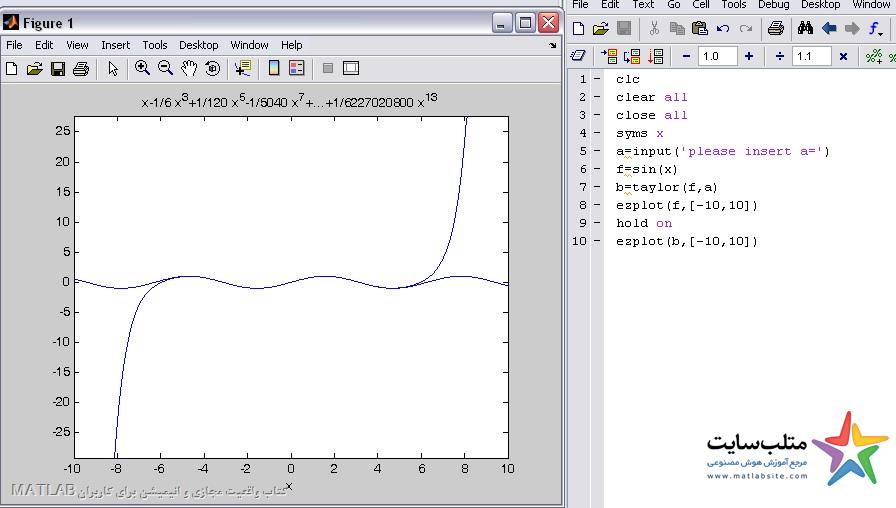
 و برای اینکه دقیق بتوانیم خطا را ببینیم محدوده ی plot ها را زیاد میکنیم مطابق شکل زیر

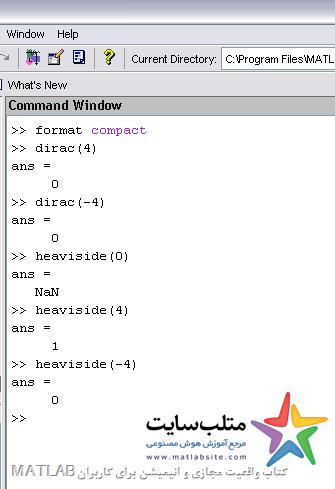
Dirac(x) ضربه
Heaviside(x)   پله

تبدیل فوریه برای توابع سمبولیک:

Fourier(f)

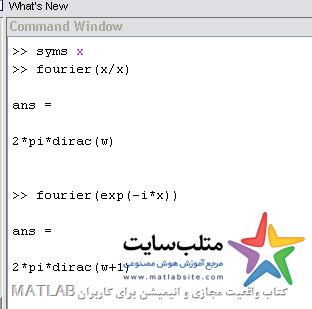
اگر  exp را فوریه بگیریم شیفت میدهد.

عکس تبدیل فوریه:

Ifourier(f)

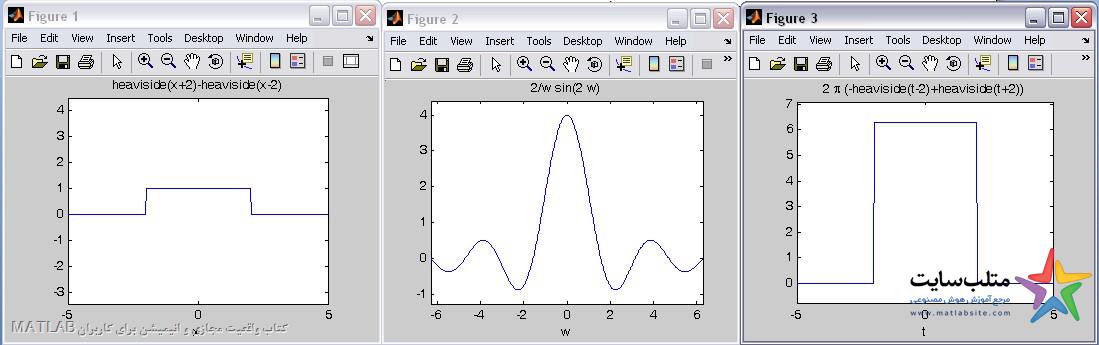
 به عنوان مثال کاربرد آن در تبدیل rect و sinc است که دوگان همند.
Sinc در متلی تعریف شده است . برای ساختن rect :

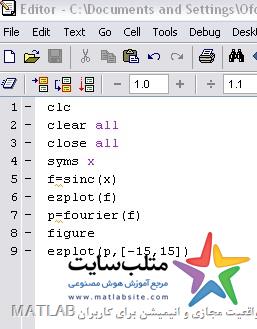
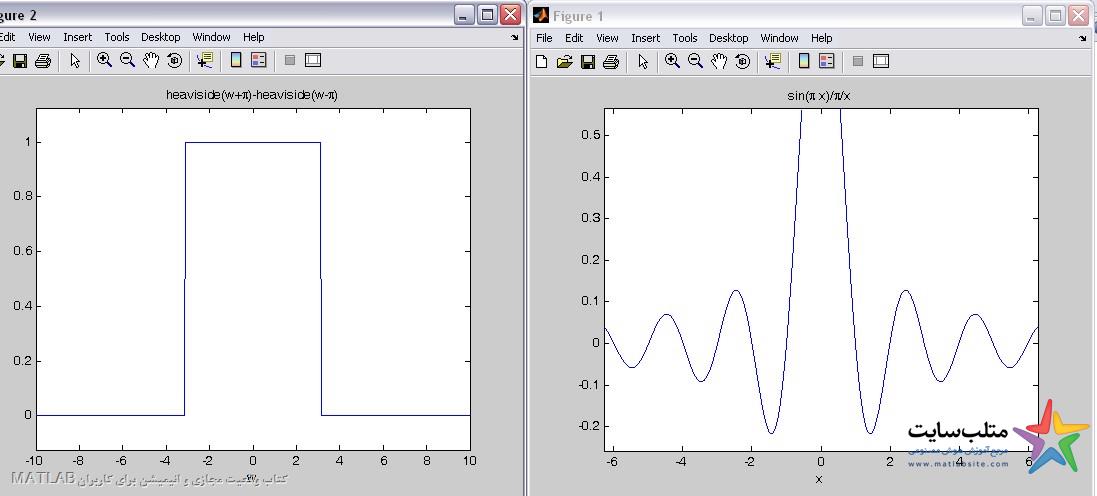
برای نشان دادن این که sinc و rect هر کدام ، تبدیل فوریه ی دیگری است ، از برنامه ی زیر استفاده میکنیم:

 
 
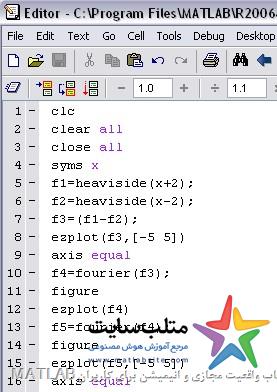
jacobian(f)
Curl()
…..و

یک سری از توابع در متلب هستند که برای موضوع های خاص به کار می روند. مثلا برای مغناطیس و…
برای مشاهده ی توابع در متلب میتوان از قسمت help متلب استفاده کرد. برای مشاهده ی توابع ابتدایی از help elfun و برای مشاهده توابع خاص از help specfun استفاده میشود.

تبدیل لاپلاس:

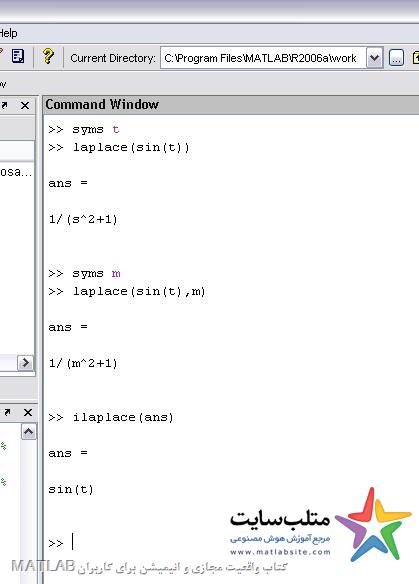
Laplace(f(t))

جواب را بر حسب متغیر s به ما می دهد.
اگر بخواهیم بر حسب ماغیر دیگری مثلا m نمایش دهد:

laplace(f(x),m)

عکس تبدیل لاپلاس:

Ilaplace(F(s))

عکس تبدیل لاپلاس غبارت زیر را به دست آورید:

(S^2+2*s+3)/(s+1)^3

 

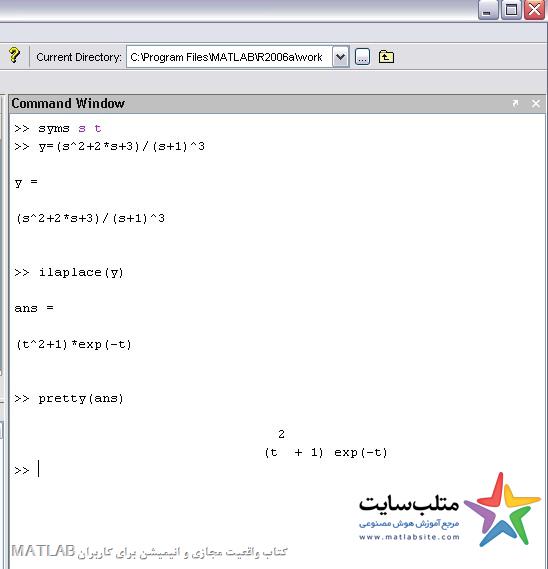
تفکیک کسر ها در متلب:

Residue(a,b)

غیر سمبولیک است و a ضرائب صورت و b ضرائب مخرج میباشد.

 

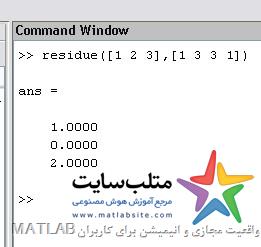
به ترتیب اول ضرائب قطب کمتر به بیشتر را می دهد. برای ریشه های مککر هم از کمترین توان می دهد.
تبدیل z:

Ztrans(f(t))
عکس تبدیل z
iztrans()

ترکیبات ۳ بعدی:
الف: توابع پیوسته (سمبلیک)

Ezplot3()

معادلات پارامتری خط یا منحنی:

Ezplot(‘x’,’y’,’z’)

چون بین دو ” قرار میدهیم سمبلیک در نظر میگیرد.
میتوانیم مختصات T را هم بدهیم:

ezplot3(‘x’,’y’,’z’,[tmin tmax])

به عنوان مثال معادله ی فنر به صورت زیر است:

 

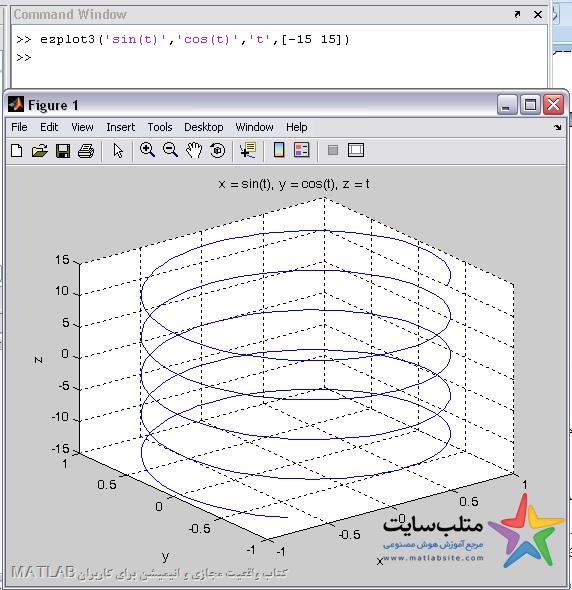
رسم سطوح سه بعدی:

Ezsurf(z)

شکل زیر مثالی است که در help متلب آمده است: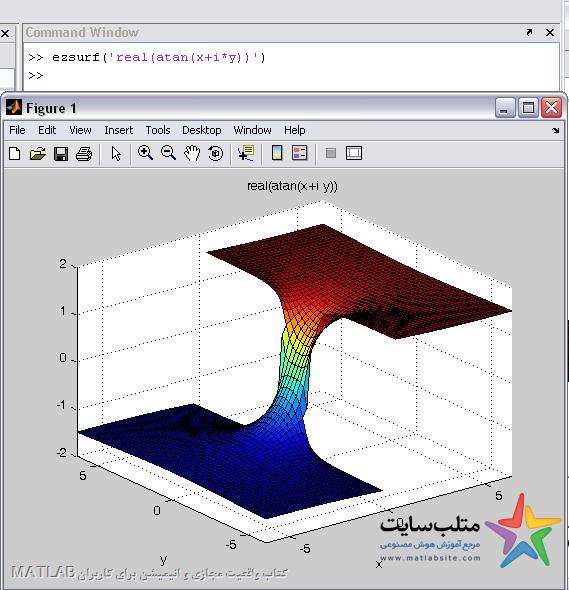

 
مثالی از رسم یک صفحه:

 

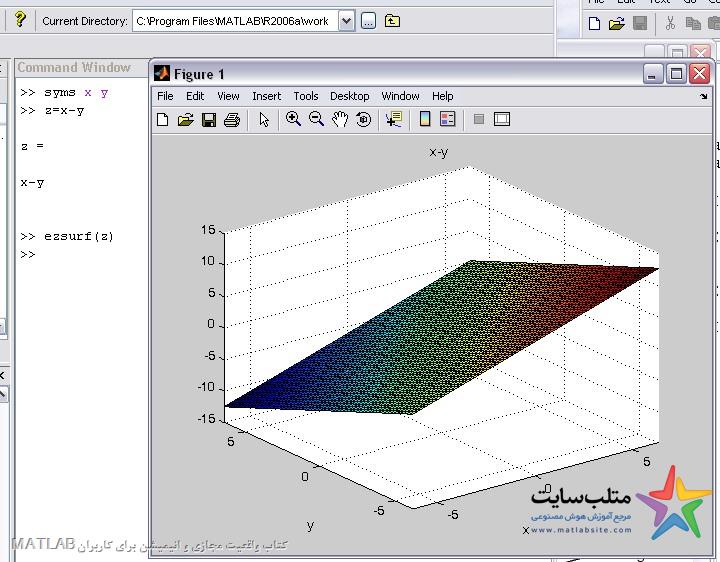
مثالی از رسم یک منحنی: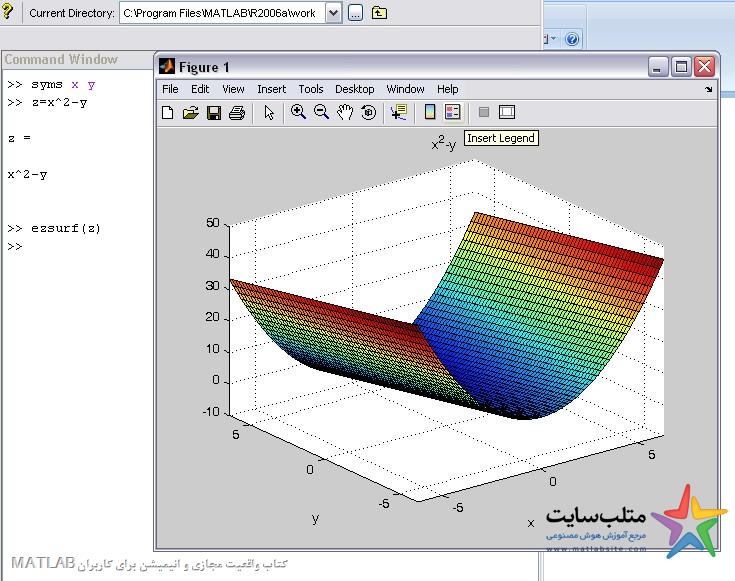

 
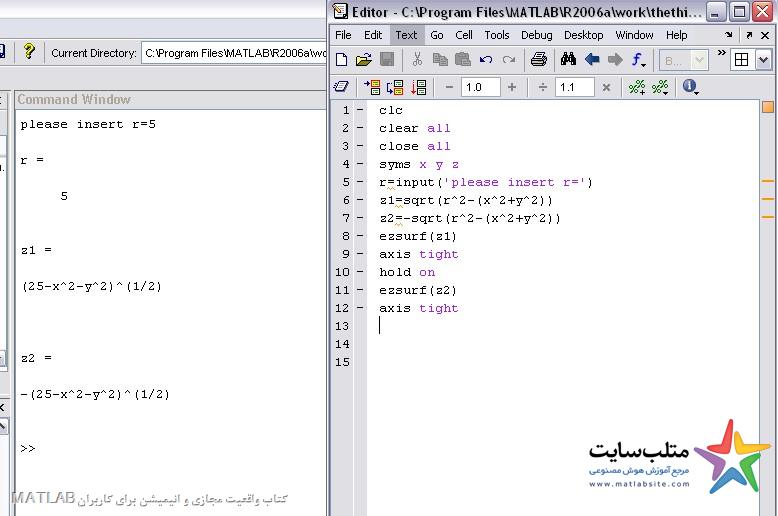
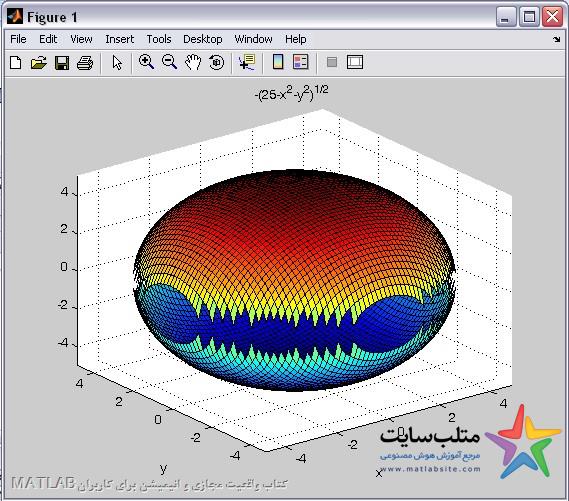
یک روش ابتدایی برای رسم کره که البته مناسب هم نیست:
شکل زیر مربوط به زمانی ست که r=5 وارد شده است: