نگاشت خود سازمان ده
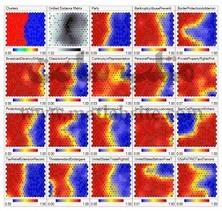
یک نگاشت خودسازمانده (SOM) یا نگاشت خودسازمانده ویژگی (SOFM)، یک نوع از شبکههای عصبی مصنوعی است که با یادگیری بدون نظارت، آموزش دیده و هدف آن تولید یک نمایش گسسته و ابعاد-پایین (اغلب دو بعدی) از فضای ورودی نمونههای آموزشی میباشد که به آن نگاشت میگویند. نگاشتهای خودسازمنده با دیگر شبکههای عصبی از این نظر متفاوت هستند که از یک تابع همسایگی برای حفظ ویژگیهای توپولوژی فضای ورودی استفاده میکنند.

یک نگاشت خودسازمانده (SOM) یا نگاشت خودسازمانده ویژگی (SOFM)، یک نوع از شبکههای عصبی مصنوعی است که با یادگیری بدون نظارت، آموزش دیده و هدف آن تولید یک نمایش گسسته و ابعاد-پایین (اغلب دو بعدی) از فضای ورودی نمونههای آموزشی میباشد که به آن نگاشت میگویند. نگاشتهای خودسازمنده با دیگر شبکههای عصبی از این نظر متفاوت هستند که از یک تابع همسایگی برای حفظ ویژگیهای توپولوژی فضای ورودی استفاده میکنند.
این قضیه SOMها را برای نمایش ابعاد-پایین از دادهی ابعاد-بالا مناسب میکند، مشابه با مقیاسپذیری چندبعدی. شبکه عصبی مصنوعی ارائه شده توسط پروفسور کوهونن در دهه ۱۹۸۰ گاهی نگاشت یا شبکه کوهونن خوانده میشود. شبکه کوهونن یک ساختار انتزاعی ساده از نظر محاسباتی است که بر روی مدلهای عصبی بیولوژیکی دهه ۱۹۷۰ و مدلهای ریختشناسی دهه ۱۹۵۰ مربوط به آلن تورینگ کار میکند.
همچون بیشتر شبکههای عصبی مصنوعی، SOMها در دو حالت کار میکنند: آموزش و نگاشت. “آموزش”، نگاشت را با استفاده از نمونههای ورودی ایجاد میکند (یک فرایند رقابتی، که کوانتیزیشن برداری نیز نامیده میشود)، در حالی که “نگاشت” یک بردار ورودی را به صورت خودکار دستهبندی میکند.
یک نگاشت خودسازمانده شامل اجزائیست که نود یا نورون نامیده میشوند. هر نود، دارای یک بردار وزن با ابعادی مشابه با بردارهای ورودی داده و یک موقعیت در فضای نگاشت است. آرایش معمول نودها در یک فضای شبکه ای دو بعدی شش ضلعی یا مثلثی است که نودها با فاصله منظم از یکدیگر در آن قرار گرفتهاند. نگاشت خودسازمانده، نگاشتی از یک فصای ورودی ابعاد بالا به فضای نگاشتی با ابعاد پایین را ایجاد میکند. روال جایگذاری یک بردار از فضای داده ورودی به فضای نگاشت، عبارت است از یافتن نودی با نزدیکترین (کوچکترین فاصله) بردار وزن به بردار فضای داده.
درحالیکه معمول است این نوع از ساختار شبکه را به شبکههای پیشخور که در آنها نودها به یکدیگر متصل نشان داده میشوند مرتبط بدانیم، این دو نوع معماری اساسا در آرایش و اهداف با یکدیگر متفاوتاند.
بسط های مفید این شبکهها شامل استفاده از شبکه های مارپیچی که لبههای مخالف در آنها به یکدیگر متصل است و استفاده از تعداد زیادی نود میباشد.
نشان داده شده است که نگاشت خودسازمانده با تعداد نود کم، رفتاری شبیه به k-means دارد و با تعداد نود زیاد، داده را به شکل توپولوژیکی بازآرایی میکند.
استفاده از U-Matrix نیز رایج است. مقدار U-Matrix یک نود خاص برابر با میانگین فاصله بین بردار وزن نود با بردار وزن نود نزدیکترین همسایهاش است. برای مثال در یک گرید مربع میتوانیم ۴ یا ۸ نزدیکترین نود (به ترتیب، همسایگی ون-نیومن و همسایگی مور) را در نظر بگیریم، یا ۶ نزدیکترین نود را در یک گرید شش ضلعی.
SOMهای بزرگ ویژگیهایی برای استفاده در آینده دارند و برای مثال در نگاشتهای حاوی هزاران گره، امکان اجرای عملیات خوشه بندی روی خود نگاشت وجود دارد.
الگوریتم
۱- بردار وزن نودهای نگاشت را به صورت تصادفی انتخاب کن
۲- بردار ورودی (D(t را بگیر
۳- هر نود موجود در نگاشت را پوشش بده
a. از فرمول فاصله اقلیدسی برای یافتن تشابه بین بردار ورودی و بردار وزن نود نگاشت استفاده کن
b. نودی که کمترین فاصله را دارد پیدا کن (این نود که بهترین تطابق را دارد BMU خوانده میشود)
۴- نودهای همسایگی BMU را با نزدیک کردن به سمت بردار ورودی بهروزرسانی کن (شامل خود BM)
Wv(s + 1) = Wv(s) + Θ(u, v, s) α(s)(D(t) – Wv(s))
۵- S را افزایش داده و از گام ۲ دوباره تمام مراحل را انجام بده تا زمانی که s<λ
یک الگوریتم دیگر
۱- بردار وزن نودهای نگاشت را به صورت تصادفی انتخاب کن
۲- هر بردار ورودی در مجموعه داده ورودی را پوشش بده
a. هر نود موجود در نگاشت را پوشش بده
i. از فرمول فاصله اقلیدسی برای یافتن تشابه بین بردار ورودی و بردار وزن نود نگاشت استفاده کن
ii. نودی که کمترین فاصله را دارد پیدا کن (این نود بهترین تطابق را دارد و BMU خوانده میشود)
b. نودهای همسایگی BMU را با نزدیک کردن به سمت بردار ورودی به روزرسانی کن (شامل خود BMU)
Wv(s + 1) = Wv(s) + Θ(u, v, s) α(s)(D(t) – Wv(s))
۳- S را افزایش داده و از گام ۲ دوباره تمام مراحل را انجام بده تا زمانی که s<λ
مباحث مرتبط
- گاز عصبی
- شبکههای عصبی با حافظه بزرگ و قدرت بازیابی (LAMSTAR)
- SOM ترکیبی کوهونن
مراجع مطالعاتی و منابع آموزشی مهم
در این بخش، قصد داریم منابع آموزشی و مراجع مطالعاتی در زمینه نگاشت خود سازمان ده را معرفی کنیم. اگر شما نیز قصد دارید که در یک کار پژوهشی، پروژه دانشگاهی یا صنعتی، و یا در مسیر علایق شخصی تان، نگاشت خود سازمان ده را فرا بگیرید، حتما پیشنهاد می کنیم که در ادامه با ما همراه باشید.
کتابهای خارجی
 |
عنوان: Self-Organizing Maps ترجمه عنوان: نگاشت خودسازمان ده مولف: Teuvo Kohonen سال چاپ: ۲۰۰۰ انتشارات: Springer لینک دسترسی: لینک |
 |
عنوان: Self-Organizing Map Formation ترجمه عنوان: نگاشت خودسازمان ده مولف: Klaus Obermayer سال چاپ: ۲۰۰۱ انتشارات: A Bradford Book لینک دسترسی: لینک |
|
|
عنوان: Self-Organizing Neural Networks ترجمه عنوان: شبکه های عصبی نگاشت خودسازمان ده مولف: Udo Seiffert سال چاپ: ۲۰۱۴ انتشارات: Physica لینک دسترسی: لینک |
منابع آموزشی آنلاین
 |
عنوان: آموزش شبکه های عصبی رقابتی و نگاشت خود سازمان ده یا SOM مدرس: دکتر سیدمصطفی کلامی هریس مدت زمان: ۴ ساعت و ۲۷ دقیقه نحوه استفاده: دریافت به صورت لینک دانلود و بر روی DVD زبان: فارسی نحوه آموزش: تئوری و عملی ارائه دهنده: سازمان علمی-آموزشی فرادرس لینک دسترسی: لینک |
 |
عنوان: آموزش جامع ماشین های بردار پشتیبان یا SVM در متلب مدرس: دکتر سیدمصطفی کلامی هریس مدت زمان: ۴ ساعت و ۵۱ دقیقه نحوه استفاده: دریافت به صورت لینک دانلود و بر روی DVD زبان: فارسی نحوه آموزش: تئوری و عملی ارائه دهنده: سازمان علمی-آموزشی فرادرس لینک دسترسی: لینک |
 |
عنوان: مجموعه آموزش های شبکه های عصبی مصنوعی در متلب مدرس: دکتر سیدمصطفی کلامی هریس مدت زمان: ۲۷ ساعت و ۴۶ دقیقه نحوه استفاده: دریافت به صورت لینک دانلود و بر روی DVD زبان: فارسی نحوه آموزش: تئوری و عملی ارائه دهنده: سازمان علمی-آموزشی فرادرس لینک دسترسی: لینک |
مجموعه: شبکه های عصبی برچسب ها: LAMSTAR, Self-Organizing Map, SOFM, SOM, SOM ترکیبی کوهونن, گاز عصبی, نگاشت خود سازمان ده, نگاشت خودسازمانده ویژگی




 (No Ratings Yet)
(No Ratings Yet)