آموزش آرایه در ساختمان داده – مرور مفاهیم
تعریف
آرایه: به ساختمانی از داده های می گویند که تحت یک نام برای زخیره سازی داده های هم نوع استفاده می شود و هر عنصر از آرایه دارای اندیس مشخصی می باشد.

تعریف
آرایه: به ساختمانی از داده های می گویند که تحت یک نام برای زخیره سازی داده های هم نوع استفاده می شود و هر عنصر از آرایه دارای اندیس مشخصی می باشد.
تعریف آرایه در زبان c به شکل زیر است:
Type name[num];
Type : نوع داده ذخیره سازی داده ها
Num : تعداد اعضای آرایه
* اندیس های آرایه در زبان c از شماره ی ۰ تا num-1 می باشد.
آرایه ها می توانند چند بعدی نیز تعریف شوند.
به عنوان مثال :
Int balabces[11][6]
یک آرایه دو بعدی میباشد که دارای ۱۱ سطر و ۶ ستون می باشد.
و یا:
Int c[3][4][5];
آرایه c به صورت سه بعدی تعریف شده است که دارای سه صفحه از آرایه های دوبعدی ۴ در ۵ است.
نحوه ذخیره سازی در حافظه:
تمام عناصر آرایه در حافطه ی کامپیوتر به صورت پشت سر هم و قرار می گیرند که این نحوه ی ذخیره سازی باعث دسترسی سریع به هر یک از عناصر آرایه می شود.
چون در آرایه همه ی عناصر به صورت پشت سر هم و از یک نوع هستند این دسترسی سریع با داشتن آدرس اولین عنصر آرایه و اندازه ی بایت اشغال شده توسط هر عنصر ممکن می شود. ولی در ساختمان داده هایی مانند لیست پیوندی که ترتیب ذخیره عناصر مشخص نیست، سرعت دسترسی به عناصر مختلف با هم متفاوت است.
نحوه محاسبه محل هر عنصر در آرایه:
در آرایه یک بعدی x[l ..u] که نماد l حد پایین آرایه و نماد u حد بالای آرایه است. نحوه محاسبه ی مکان اندیس i از آرایه به شکل زیر است:
loc(x[i]): a+(i-l)*w
w : بیت اشغال شده توسط هر عنصر
برای آرایه های بیشتر از یک بعد با فرض اینکه عناصر آرایه به صورت سطر به سطر در حافظه ذخیره می شوند، محل قرار گیری هر عنصر از آرایه در حافظه به کمک رابطه ی زیر انجام می شود.
آرایه دو بعدی:
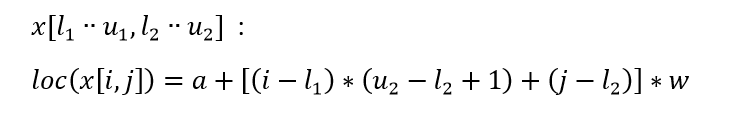
آرایه سه بعدی:
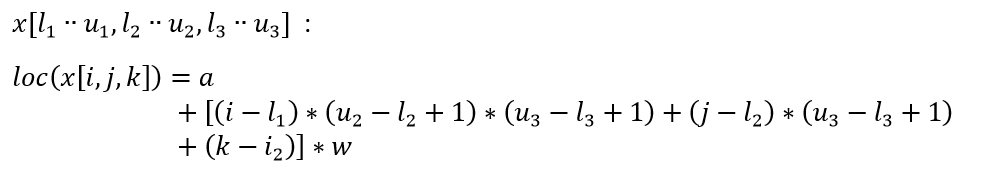
مثال :
اگر آرایه A به صورت A[20][10][5] باشد. با فرض اینکه هر int چهار بایت فضا لازم دارد و آدرس شروع آرایه صفر باشد، آدرس عنصر A[3][4][2] را بدست آورید.
پاسخ:
۰+[(۳-۰)+(۴-۰)*۲۰+(۲-۰)*۲۰*۱۰]*۴=۱۹۳۲
انواع عملیاتهای مهم روی آرایه :
جست و جو
- خطی
- دودویی
- سه تایی (ترنری)
درج
حذف
۱- جست و جوی خطی
یکی از الگوریتم هایی که برای جستجوی یک سری داده وجود دارد جستجوی ترتیبی یا جستجوی خطی است. این الگوریتم کلیه عناصر درون یک لیست را یکی یکی بررسی میکند تا آرگومان جستجو پیدا شود.
این الگوریتم جزو ساده ترین الگوریتمهای جستجو میباشد که در یک جست و جوی ناموفق n+1 عمل مقایسه انجام میدهد که مرتبه ی زمانی آن o(n) است.
قطعه کد زیر الگوریتم جست و جوی خطی می باشد که در صورت پیدا کردن key اندیس خانه حاوی آن و در غیر این صورت عدد ۱- را برمیگرداند.
LinearSearch(data[], n , key) {
for (i = 0; i < n-1; i++)
if (data[i] == key)
return i;
return -۱;
}
۲- جست و جوی دودویی:
الگوریتم جستجوی دودویی، تکنیکی است برای یافتن یک مقدار عددی از میان مجموعهای از اعداد مرتب. این متد محدوده ی جستجو را در هر مرحله به نصف کاهش میدهد، بنابراین هدف مورد نظر یا به زودی پیدا میشود و یا مشخص میشود که مقدار مورد جستجو در فهرست وجود ندارد و این الگوریتم از مرتبه ی زمانی o(log n) می باشد.
* جستجوی دودویی فقط در آرایه های مرتب استفاده می شود.
در این روش عنصر مورد نظر با خانه وسط آرایه مقایسه می شود اگر با این خانه برابر بود جستجو تمام می شود اگر عنصر مورد جستجو از خانه وسط بزرگتر بود جستجو در بخش بالایی آرایه و در غیر این صورت جستجو در بخش پایینی آرایه انجام می شود (فرض کرده ایم آرایه به صورت صعودی مرتب شده است) این رویه تا یافتن عنصر مورد نظر یا بررسی کل خانه های آرایه ادامه می یابد.
BSearch(A[], value, low, high) {
if (high <low)
return -1
mid = low + ((high – low) / 2)
if (A[mid]> value)
return BSearch(A, value, low, mid-1)
else if (A[mid] <value)
return BSearch(A, value, mid+1, high)
else
return mid // found
}
۳- درج در آرایه
تابع insert ، مقدار x را در مکان k ام آرایه a ، اضافه می کند.
فرض شده که در آرایه a دارای n خانه است که m عنصر آن پر است
Insert(a[], m, k, x)
For (i=m-1; i>=k; i–) عملیات شیفت دادن داده ها //
a[i+1] = a[i]
a[k] = x
۴- حذف از آرایه
تابع زیر k امین عنصر از آرایه را حذف کرده و آن را برمیگرداند.
Delete(a[], n, k)
x = a[k]
For (i=k; i<=n-1;i++)
a[i] = a[i+1]
a[i] = 0
return x
* مرتبه زمانی الگوریتم های درج و حذف خطی است.
۱- ماتریس اسپارس:
ماتریس اسپارس یا خلوت به ماتریسی گفته می شود که دارای تعداد زیادی صفر است. در این ماتریس، برای کاهش حافظه مصرفی و زمان اجرا فقط عناصر غیر از صفر ماتریس ذخیره میشوند.
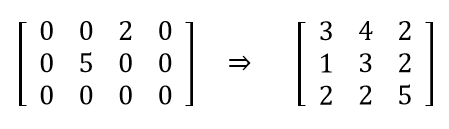
برای ذخیره کردن ماتریس اسپارس در حافظه، از یک ماتریس سه ستون در n سطر استفاده می شود. که n تعداد اعداد غیر صفر موجود در ماتریس اسپارس است.
در سطر اول این ماریس به ترتیب سطر، ستون و تعداد اعداد غیر صفر ماتریس اصلی ذخیره میشود.
و در n سطر بعدی، در هر سطر شماره ی سطر، شماره ستون و مقدار یکی از اعداد وجود دارد.
مجموعه: دستهبندی نشده




 (No Ratings Yet)
(No Ratings Yet)