شبکه های عصبی هاپفیلد — مرور مفاهیم

شبکه های هاپفیلد:
ما در شبکه های دیگر یکسری ورودی و خروجی داشتیم که می دادیم به شبکه عصبی و با آن آموزش می دیدیم در هاپفیلد یکسری الگو الگو باید بدهیم تا آن بتواند با استفاده از آن الگوها سیستم را به آن الگو برساند. توجه شود که در هاپفیلد تمام ارتباطات در شبکه هاپفیلد دوطرفه و متقارن هستند.

شبکه های هاپفیلد:
ما در شبکه های دیگر یکسری ورودی و خروجی داشتیم که می دادیم به شبکه عصبی و با آن آموزش می دیدیم در هاپفیلد یکسری الگو الگو باید بدهیم تا آن بتواند با استفاده از آن الگوها سیستم را به آن الگو برساند. توجه شود که در هاپفیلد تمام ارتباطات در شبکه هاپفیلد دوطرفه و متقارن هستند.
از دو دیدگاه می توان شبکه های عصبی هاپفیلد را بررسی کرد
۱٫از دیدگاه سیستم های مکانیکی از این نظر چیزی جز یک معادله دیفرانسیل گسسته یا پیوسته زمان نیست و یک بحث ریاضی می باشد
۲٫اما از جهت دیگر یک شبکه عصبی است منتها به صورت یک حافظه شبکه عصبی که به صورت یک حافظه عمل می کند و یکسری الگو ها را در خودش ذخیره می کند.
بنابراین از دیدگاه دوم شبکه هاپفیلد در هنگام مواجه با یکسری ورودی ها که منطبق یا غیر منطبق بر الگوهای ذخیره شده باشد سعی می کند آن چیزهایی را که می بیند به سمت یکی از این الگوها گرد کند.مثل وقتی که دست خط یک نفر را می خوانیم چون همه ی افراد به یک شکل نمی نویسند ولی همه ی ما یک مفهوم را از آنها درک می کنیم.

شکل ۱) شبکه هاپفیلد با ۴ نرون
شکل بالا یک شبکه هاپفیلد می باشد که از نوع شبکه های عصبی دینامیکی می باشد. در واقع هر سیستمی که حالت فعلی اش به حالت لحظه قبلش وابستگی داشته باشد را سیستم دینامیکی می گویند که با یکسری بلوک تاخیر یا مشتق گیر شبیه سازی می کنند.
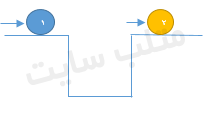
برای درک این موضوع که حالت سیستم مهم است مثال بالا را در نظر بگیرید. فرض کنید در بازی گلف در حالت (۱) ما به توپ ضربه ای می زنیم و توپ به گل می رود. در حالت (۲) اگر ما یک توپ دیگر داشته باشیم و در همین جهت به آن نیرو وارد کنیم آیا باز به هدف خواهد رسید؟ خیر بلکه از هدف دور خواهد شد بنابراین حالت سیستم خیلی مهم است و باید بدونیم در چه حالتی چه نیرویی را وارد می کنیم.در حالت کلی یک معادله برای سیستم بالا در نظر می گیرند که به شکل زیر است.
![]()
رابطه بالا نشان می دهد که حالت سیستم در لحظه ی بعد تابعی از حالت قبلی سیستم و ورودی که به آن وارد می شود. البته در مسائل پیوسته زمان نمی توان لحظه ی بعد را مشخص کرد بنابراین معادله به شکل زیر تغییر می کند.
![]()
جهت اثبات رابطه بالا فرض کنید واحد زمانی ما ∆t می باشد در ادامه بسط تیلور x(t+∆t) را می نویسیم بعد از طرفین وسطین کردن معادله نهایی بدست می آید پس تعمیمی از حالت گسسته می باشد. وقتی ∆t به سمت صفر میل کند بسط تیلور با دو جمله اولش به خوبی تخمین زده می شود. معادلات زیر روند کار را نشان می دهد.
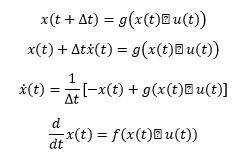
حال این سیستم دینامیکی می تواند یک شبکه عصبی باشد.
عملا شبکه عصبی هاپفیلد یک سیستم دینامیک است. بنابراین ابتدا در مورد رفتارهای سیستمی دینامیک اشاراتی می کنیم و در ادامه به این می رسیم که شبکه عصبی هاپفیلد چگونه تعریف می شود. معادله (۶) یک سیستم غیر خطی ساده است اصولا برای این سیستم می توان یکسری نقاطی را در نظر گرفت که اگر سیستم به آن نقاط برسد دیگر تمایلی به تغییر حالت ندارد که این نقاط را نقطه ی تعادل گویند.
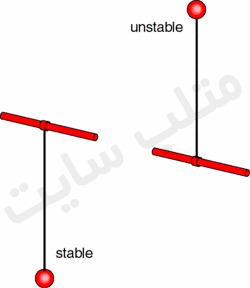
آونگ
مطابق شکل اگر آونگ را در وضعیت ۹۰ درجه قرار دهیم دیگر تمایلی به حرکت ندارد ولی اگر اندگی به آن نیرو وارد کنیم آنقدر نوسان می کند تا به تعادل برسد که این نقطه را نقطه ی تعادل می گویند.شکل زیر نقاط تعادل سیستم را در حالتی نشان می دهد که در معادله x ̇=f(x) مقدار f(x)=0 باشد که برای آن یک ماتریس ژاکوبین تشکیل داده و رابطه r^2 – 4∆=۰ را شکل داده و نقاط تعادل را بررسی می کنند.
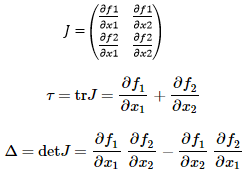
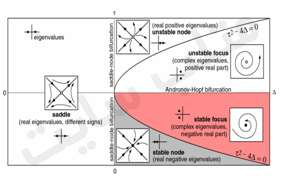
اصولا ما در طراحی سیستم ها و کنترل آنها علاقه مند هستیم یکسری نقاط تعادل پایدار تعریف کنیم در واقع ما این نقاط را برای شبکه هاپفیلد ایجاد کرده که هر کدام از این نقاط یکسری ناحیه جذب دارند منتها اینکه نقاط تعادل کجا باشند در بحث طراحی شبکه به آن خواهیم رسید. به عنوان مثال اگر بخواهیم حروف الفبای انگلیسی را تشخیص دهیم باید ۲۶ تا نقطه ی تعادل داشته باشیم که اینها در واقع حافظه هستند. در ادامه به مفهوم نرون هایی که به شکل دایره کشیده شده اند می پردازیم
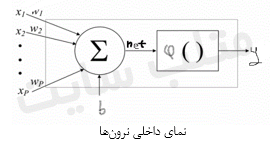
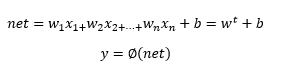
حال اگر بخواهیم روابط شکل ۱ را به صورت معادله بنویسیم
![]()
در رابطه بالا حال به آینده ارتباط پیدا کرد بنابراین معادله دینامیکی داریم. که در آن خروجی بخش سیگنال net نرون i ام در لحظه t برابر است با مجموع وزن دار یکسری از ورودی ها و یک بایاس که به این رابطه معادله حالت می گویند.
![]()
رابطه بالا را معادله خروجی یا معادله تصمیم گویند که حالت سیستم را به طریقی به متغیری که ما مشاهده می کنیم ربط می دهد.حال دو معادله بالا را جمع بندی می کنیم
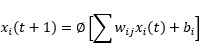
بنابراین شبکه عصبی در حالت کلی چند تا از این معادلات تفاضلی یا دیفرنس می باشد. معادله قبلی یک معادله دینامیکی است و می توانیم تا آینده دور پیش برویم. در ادامه در مورد شبکه هاپفیلد در حالت پیوسته صحبت می کنیم که فقط کافیست به جای آنجایی که t+1 است مشتق بگذاریم
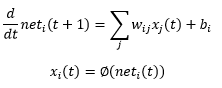
در شکل ۱ سیستم در حالت اولیه کارش را شروع می کند و این ها اینقدر می گردند و در زمان پیشرفت می کنند که عملا یکی از این نرون ها همیشه پیروز می شود و همیشه یک رفتار ثابت از خودش نشان می دهد یعنی به یک تعادل می رسد.
سوال: اصولا یک نقطه ی تعادل کی می تواند پایدار باشد؟
چرا جسمی را رها کنیم می افتد؟
دلیلش این است که می خواهد انرژی پتانسیل به جنبشی تبدیل شود یا به عبارتی دیگر می خواهد انرژی از دست بدهد می خواهد به کم ترین مقدار انرژی برسد ما هم در طراحی شبکه هاپفیلد یک مفهومی مثل انرژی تعریف می کنیم و سعی می کنیم این نقاط تعادلمون کم ترین انرژی ممکن را داشته باشد.
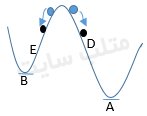
مطابق شکل بالا وقتی سیستم از نزدیک یک نقطه ی تعادل حرکت می کند به آن نقطه نزدیک می شود گرچه که ناحیه جذب A بیش تر از B می باشد.حال مفهومی از انرژی را در شبکه های عصبی هاپفیلد تعریف می کنیم که به شکل زیر می باشد.
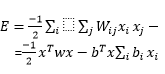
می خواهیم یک تمهیدی را نظر بگیریم که به ازای نقاط تعادل مطلوب E به کم ترین مقدار هم که برسه حداقل نسبت به نقاط همجوار یک مینیمم نسبی را داشته باشد که اینجا بحث همگرا شدن پیش می آید.توجه شود که اسم E را اینجا به خاطر ارتباط نزدیکی که با مفهوم انرژی در سیستم های واقعی دارد E گذاشتیم و بحث پایداری که انجام دادیم بسیار مهم است چرا که ما دوست داریم نهایتا با استفاده از این شبکه عصبی به یک تعدا نقاط پایدار برسیم. اگر پایداری سیستم تضمین نشده باشد اینها به جایی که به نقاط تعادل نزدیک شوند از آن دور می شوند. حال این کار به چه صورت انجام می شود؟ یک ریاضی دان به نام لیاپانوف قضیه ای را در مورد پایداری سیستم های غیرخطی بیان می کند که بیان می کند برای یک سیستم غیرخطی نقاط تعادل مختلفی را می توان در نظر گرفت که در رابطه ی x ̇=f(x) پاسخ های f(x)=0 نقاط تعادل ما می شود.فرض کنید یکی از این نقاط x_0 باشد می خواهیم ببینیم این نقطه پایدار است یا نه؟ طبق قضیه لیاپانوف اگر تابع v(x) شرایط زیر را داشته باشد این تابع به معنای لیاپانوفی پایدار است.
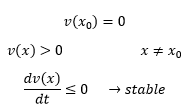
مفهوم رابطه (dv(x))/dt≤۰ این است که در همه ی زمان ها دارد کم می شود یا حداقل ثابت است یعنی از نقطه ی همگرایی اش دور نمی شود پس سیستم از بیرون انرژی نمی گیرد بلکه از دست می دهد که اینها از این رابطه مشخص می باشد.حال می خواهیم ببینیم آیا می توان E را به عنوان یک تابع لیاپانوف برای سیستم در نظر گرفت. یا به عبارتی آیا مشتق E در زمان منفی است؟
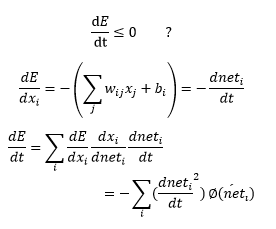
بنابراین تابع ∅ باید صعودی باشد تا شزط لیاپانوف عملی شود و تابع ∅ می تواند مثل توابع زیر باشد:
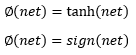
حال می خواهیم همه ی روابط را جمع بندی کنیم تا برسیم به چیزی که به عنوان شبکه هاپفیلد آن را می شناسیم.در اینجا به جای تابع ∅ از تابع sign استفاده می کنیم. نهایتا رابطه ی زیر در واقع یک شبکه ی عصبی هاپفیلد را نشان می دهد:
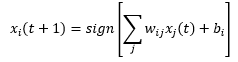
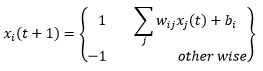
حال سوال این است که پارامترهای این شبکه شامل w وb چگونه تعیین می گردد که در ادامه به آن می پردازیم.برای اینکار دو روش وجود دارد که ما همان روش استفاده از قانون هب را دنبال می کنیم.واقعیت این است که در رابطه انرژی می توان گفت x_i نقش ورودی و x_j نقش خروجی را دارد و طبق قانون یادگیری هب ∆w=ηyx پس تغییرات ∆w به صورت زیر می باشد که در اینجا از δ به جای x استفاده می شود.
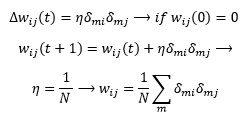
حال رابطه را به صورت برداری می نویسیم:
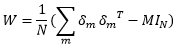
حال می خواهیم مقدار b را بدست بیاوریم. می خواهیم
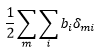
ماکزیمم شود.حال چون بعد ها، b ها از هم مستقل هستند می توانیم فقط روی یکi بخصوص تکیه کنیم بنابراین باید![]()
![]() اما چون مقداری بزرگ می شود مقدار b برابر است با میانگین الگوهایی که در حافظه باید باشد. در نتیجه مقدار b برابر است با :
اما چون مقداری بزرگ می شود مقدار b برابر است با میانگین الگوهایی که در حافظه باید باشد. در نتیجه مقدار b برابر است با :
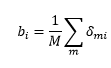
ماشین بولتزمن:
ما نشان دادیم که در شبکه هاپفیلد این قاعده است که
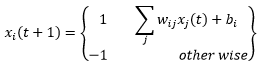
که این یک عملکرد قطعی است . اما وقتی که از بولتزمن استفاده می کنیم دقیقا همینه فقط این به صورت احتمالی بیان می شود یعنی احتمال یک شدن در لحظه ی بعدی برابر است با
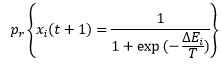
مقدار ![]() یعنی اختلاف انرژی که وجود دارد. که در خود هاپفیلد اگر مقدار
یعنی اختلاف انرژی که وجود دارد. که در خود هاپفیلد اگر مقدار ![]() باشد یک در نظر می گیریم ولی در بولتزمن این ترم تغییرات انرژی را وارد یک معادله ای می کنیم و احتمال یک شدن را حساب می کنیم حال اگر مقدار
باشد یک در نظر می گیریم ولی در بولتزمن این ترم تغییرات انرژی را وارد یک معادله ای می کنیم و احتمال یک شدن را حساب می کنیم حال اگر مقدار ![]() باشد یعنی اگر روی مرز باشیم مثل این می ماند که یک سکه ای را پرتاب می کنیم که از نظر پلانک عدم قطعیت کامل است. اما اگر
باشد یعنی اگر روی مرز باشیم مثل این می ماند که یک سکه ای را پرتاب می کنیم که از نظر پلانک عدم قطعیت کامل است. اما اگر ![]() باشد احتمال یک شدن صفر می شود یعنی به هیچ وجه نمی تواند یک باشد. اگر
باشد احتمال یک شدن صفر می شود یعنی به هیچ وجه نمی تواند یک باشد. اگر
![]() یعنی قطعا یک می شود ولی اگر بین اینها باشد به تصادف انتخاب می شود. ولی اگر
یعنی قطعا یک می شود ولی اگر بین اینها باشد به تصادف انتخاب می شود. ولی اگر ![]() باشد احتمال یک شدن بیشتر می باشد. بنابراین بولتزمن یک شبکه تصادفی است.در این شبکه عصبی وقتی تغییرات انرژی مطلوب ما باشد به سمت یک شدن جلو می رویم وقتی نامطلوب ما باشد به سمت ۱ جلو می رویم.
باشد احتمال یک شدن بیشتر می باشد. بنابراین بولتزمن یک شبکه تصادفی است.در این شبکه عصبی وقتی تغییرات انرژی مطلوب ما باشد به سمت یک شدن جلو می رویم وقتی نامطلوب ما باشد به سمت ۱ جلو می رویم.
مثال:
یکی از مسائل معروفی که با ماشین بولتزمن و شبکه هاپفیلد حل شده مسئله فروشنده دوره گرد یا tsp است که ما در مورد این صحبت می کنیم که این را چطوری به خورد شبکه عصبی می دهند. در واقع می آیند تابع انرژی را طوری تعریف می کنند که مینیمم شدن مقدار اون انرژی مترادف باشد با بهینه شدن حل اون مسئله ای که به tsp معروف است. در مسئله tsp صحبتمان سر این است که یک مسیری را طی بکنیم که از همه ی شهرها عبور بکند و کوتاه ترین طول ممکن را داشته باشد.
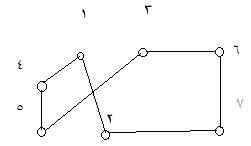
این چیزی که به اسم مسئله ی tsp داریم را می توان به صورت یک مسئله ی باینری توصیف کرد. فرض کنید مسیری که می خواهیم شروع کنیم شهر ۳ باشد (۳،۶،۷،۲،۱،۴،۵) این مسیر را می توان با یک ماتریس نشان داد که هر سطر مربوط به یک شهر و هر ستون مربوط به یک موقعیت است ما می خواهیم این مسیر را به صورت باینری نمایش دهیم الان شهر ۳ در موقعیت اول است در واقع ماتریس رو به رو یک کدینگ باینری از این مسئله است اما محدودیت هایی که داریم این است که باید روی هر سطر فقط یک عدد ۱ باشد و کم تر از این هم نمی تواند باشدو همچنین روی هر ستون، در کل ما هفت تا یک داریم یا به عبارتی اگر n تا شهر داشته باشیم باید n تا یک داشته باشیم. وقتی می گوییم v_15=1 است یعنی شهر ۱ در موقعیت پنجم ملاقات می شود.در ادامه یک تابع انرژی که تمامی این قیود را داشته باشد که فقط و فقط یک عدد ۱ روی این سطرها داشته باشیم کافیست تابع انرژی را به صورت زیر تعریف کنیم:
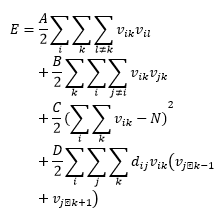
قسمت(۱) معادله بالا:
برای اینکه به ازای هر کدام از این سطرها مثلا سطر i برای اینکه در این سط فقط یک عدد ۱ داشته باشیم و دو تا ۱ نداشته باشیم باید دو به دو اینها را در هم ضرب کنیم و با هم جمع کنیم صفر بدست آید و از آنجایی که هر درایه ماتریس نباید در خودش ضرب شود شرط l≠k را می گذاریم و این رابطه باید کمینه شود یعنی اینجا صفر شود منتها این را با یک وزنی در نظر می گیرند به خاطر اینکه k وl دو بار با هم سنجیده می شود ضریب ۰٫۵ را می گذاریم.
قسمت(۲) معادله:
برای ستون ها است که البته اینجا برای یک k به خصوص جلو می رویم.
قسمت(۳) معادله:
برای اینکه در مجموع روی این ماتریس n تا ۱ داشته باشیم می آییم ![]() را برای انحراف در نظر می گیریم که هر جوری که این انحراف پیدا کند باعث می شود
را برای انحراف در نظر می گیریم که هر جوری که این انحراف پیدا کند باعث می شود ![]() بیش تر شود
بیش تر شود
قسمت(۴) معادله:
اگر بخواهیم طول ها را در نظر بگیریم هر شهر باید فاصله اش با شهر بعدی در نظر گرفته شود منتها نمیدانیم که شهر بعدی اش چیه لذا باید به ازای هر دوتا شهر I,j کافیه که این دوتا شهر یکی بعد از دیگری باشد و باید فاصله ی d_ij را جمع کنیم اما به چه صورت؟ رابطه نشان می دهد که j یا قبل از i است یا بعد از i است.
حال اگر یک شبکه عصبی هاپفیلدی طراحی کنیم که تابع انرژی اش این باشد آن شبکه عصبی هاپفیلد را یک ماتریس بدهیم ختم می شود به یک ماتریس که تمام شرایط را دارد که نقطه ی تعادل ما همان پاسخ بهینه ما است.
نکته آخر اینکه ماشین بولتزمن در یک مینیمم محلی نمی افتد چون هر لحظه عملکردش تصادفی است.
مجموعه: اخبار و تازه ها




 (No Ratings Yet)
(No Ratings Yet)