«توزیع احتمال» (Probability Distribution)، چگونگی توزیع مقادیر متغیرهای تصادفی را نشان می‌دهد. در واقع، توزیع احتمال یک تابع آماری است که همه مقادیر ممکن و «درست‌نمایی‌هایی» (Likelihood) که یک متغیر تصادفی می‌تواند در یک طیف خاص بگیرد را نشان می‌دهد. در یک توزیع احتمال اگر مجموعه مقادیر خروجی احتمالی حاوی مقادیر گسسته باشند، «گسسته» (Discrete) (پرتاب سکه که در آن خروجی یک پرتاب یا شیر است یا خط) و اگر مجموعه خروجی‌های احتمالی حاوی مقادیر حقیقی باشند، «پیوسته» (Continuous) (برای مثال، میزان رطوبت در یک روز) است. یک توزیع نرمال (گاوسی)، یک توزیع احتمال پیوسته است.

توزیع نرمال گاهی با عنوان منحنی زنگوله‌ای نیز شناخته می‌شود. توزیع نرمال به وسیله تابع چگالی زیر تعریف می‌شود:

در تابع بالا، μ میانگین جامعه، σ انحراف معیار و σ۲ واریانس است. در ادامه، قطعه کد پایتون لازم برای ساخت یک توزیع نرمال (میانگین = ۵، انحراف معیار = ۲) ارائه شده است.

“””
Normal Distribution
Author: Balamurali M
“””

import numpy as np
import matplotlib.pyplot as plt

class norm1:
def __init__(self, a1, b1, c1):
self.a1 = a1
self.b1 = b1
self.c1 = c1

def dist_curve(self):
plt.plot(self.c1, 1/(self.b1 * np.sqrt(2 * np.pi)) *
np.exp( – (self.c1 – self.a1)**2 / (2 * self.b1**2) ), linewidth=2, color=’y’)
plt.show()

#Vary the mean and SD to generate different plots
mean1 = 5
sd1 = 2

c = np.random.normal(mean1, sd1, 3000)

w1, x1, z1 = plt.hist(c, 100, normed=True) #hist

hist1 = norm1(mean1, sd1, x1)
plot1 = hist1.dist_curve()

پس از اجرای کد، نمودار زیر ایجاد می‌شود. محور X نشان‌گر متغیر تصادفی و محور Y نشان‌گر احتمال مشاهده هر مقدار است. می‌توان مشاهده کرد که نوک زنگوله روی عدد ۵ است (وسط ۴ و ۶ که میانگین است).

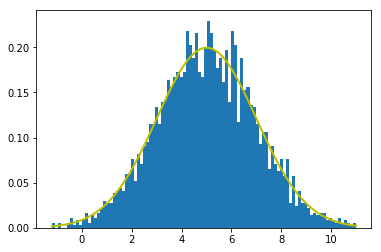
توزیع نرمال استاندارد حالت خاصی از توزیع نرمال محسوب می‌شود که در آن μ = ۰ و σ = ۱ است (میانگین برابر با صفر و انحراف معیار برابر با یک است). در ادامه، کد پایتون لازم برای ساخت توزیع نرمال استاندارد ارائه شده است. این کد مشابه کدی است که پیش‌تر ارائه شد، با این تفاوت که میانگین برابر با صفر و انحراف معیار برابر با یک قرار داده شده است.

# -*- coding: utf-8 -*-
“””
Standard Normal Distribution
Author: Balamurali M
“””

import numpy as np
import matplotlib.pyplot as plt

class norm1:
def __init__(self, a1, b1, c1):
self.a1 = a1
self.b1 = b1
self.c1 = c1

def dist_curve(self):
plt.plot(self.c1, 1/(self.b1 * np.sqrt(2 * np.pi)) *
np.exp( – (self.c1 – self.a1)**2 / (2 * self.b1**2) ), linewidth=2, color=’y’)
plt.show()

#mean 0 and sd 1 for the standard normal distribution
mean = 0
sd = 1

c = np.random.normal(mean, sd, 3000)

w1, x1, z1 = plt.hist(c, 100, normed=True) #hist

hist1 = norm1(mean, sd, x1)
plot1 = hist1.dist_curve()

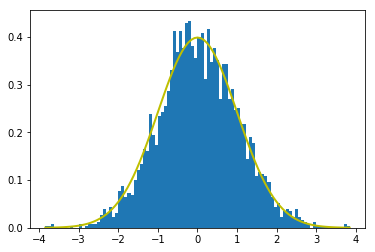
همانطور که از تصویر مشهود است، میانگین صفر است و نوک زنگوله روی صفر قرار دارد. برخی از ویژگی‌های توزیع نرمال استاندارد در زیر بیان شده‌اند:

۱. منحنی نرمال حول محور میانگین متقارن است و شکل زنگوله مانندی دارد.

۲. میانگین، مد و میانه در توزیع نرمال استاندارد برابر با صفر و مرکز نمودار هستند.

۳.  تقریبا ٪۶۸ از داده‌ها بین -۱ و +۱ قرار دارند (با ۱ انحراف معیار از میانگین)، ٪۹۵ بین -۲ و +۲ (با ۲ انحراف معیار از میانگین) و ٪۹۹.۷ از داده‌ها بین -۳ و +۳ قرار دارند (با انحراف معیار ۳ از میانگین). در ادامه، برخی از اصطلاحات متداول استفاده شده در این مطلب، بیان شده‌اند.

جامعه: فضای همه عناصر ممکن از یک مجموعه از داده‌ها

نمونه: شامل مشاهداتی است که از جامعه به دست آمده‌اند.

پارامتر: یک مشخصه قابل اندازه‌گیری از جامعه مانند میانگین و انحراف معیار است.

آماره: مشخصه قابل اندازه‌گیری از یک نمونه را گویند.

پیش از پایان این مطلب، لازم است به «قضیه حد مرکزی» (Central Limit Theorem) نیز اشاره شود. یکی از دلایل اهمیت بسیار بالای توزیع نرمال، قضیه حد مرکزی است. بر اساس این نظریه، توزیع نمونه‌ها از میانگین نمونه در یک جامعه داده شده نرمال خواهد بود، اگر سایز نمونه بزرگ باشد. حتی اگر توزیع جامعه اصلی نرمال نباشد، توزیع نمونه جدید نرمال خواهد بود (با افزایش اندازه نمونه). عملا، سایز نمونه ۳۰ و بیش‌تر از آن، بزرگ محسوب می‌شود.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار و احتمالات
• آموزش تکمیلی برنامه‌نویسی پایتون
• مجموعه آموزش‌های برنامه‌نویسی پایتون Python
• زبان برنامه‌نویسی پایتون (Python) — از صفر تا صد
• یادگیری علم داده (Data Science) با پایتون — از صفر تا صد
• توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها

 

منبع [+]