فصل سوم کتاب: بهینه کنترل فعال سازه با رویکرد کلاسیک و هوش مصنوعی

۳-۱- مبانی ورودی های لرزه ای سازه ها
ورودیهای لرزهای، دادههای زمین لرزه هستند که برای انجام انواع تحلیلهای لرزهای به کار میروند. در فرآیند تحلیل و طراحی لرزهای سازهها، به دادههای لرزهای گوناگون بسته به نوع تحلیل نیاز است. این دادهها به دو شیوه قطعی یا احتمالاتی در دسترس قرار میگیرند. ورودیهای لرزهای قطعی برای تحلیل و طراحی قطعی سازهها به کار میروند، و ورودیهای احتمالاتی در تحلیل ارتعاشی سازهها در برابر نیروهای زمین لرزه، تحلیل خطر پذیری لرزهای سازهها، و برآورد آسیب لرزهای زلزلههای آینده کاربرد دارند. ورودیهای لرزهای برای تحلیل سازهها، در حوزه زمان یا در حوزه بسامد و یا همزمان در هر دو حوزه زمان و بسامد گزارش میشوند. افزون بر این، شماری از سنجههای زمین لرزه به عنوان ورودی و برای تکمیل اطلاعات لازم برای انجام تحلیلهای گوناگون به کار میروند. بزرگا، شدت، بیشینه جا به جایی، سرعت، شتاب زمین، مدت (زمان تداوم)، بسامد غالب و … نمونههایی از این سنجهها هستند. همچنین، در برخی تحلیلها مانند تحلیل خطر پذیری لرزهای، برآورد آسیب سازهها، و تحلیل احتمالاتی لرزهای، پیش بینی شناسههای ورودی لرزهای مربوط به زلزلههای آینده ضروری است. این پیش بینیها به صورت معادلههایی تجربی ارائه میشوند. در این فصل، انواع مختلف ورودیهای لرزهای و شماری از رابطههای پیش بینی پر کاربرد، بررسی خواهند شد.

۳-۱- مبانی ورودی های لرزه ای سازه ها
ورودیهای لرزهای، دادههای زمین لرزه هستند که برای انجام انواع تحلیلهای لرزهای به کار میروند. در فرآیند تحلیل و طراحی لرزهای سازهها، به دادههای لرزهای گوناگون بسته به نوع تحلیل نیاز است. این دادهها به دو شیوه قطعی یا احتمالاتی در دسترس قرار میگیرند. ورودیهای لرزهای قطعی برای تحلیل و طراحی قطعی سازهها به کار میروند، و ورودیهای احتمالاتی در تحلیل ارتعاشی سازهها در برابر نیروهای زمین لرزه، تحلیل خطر پذیری لرزهای سازهها، و برآورد آسیب لرزهای زلزلههای آینده کاربرد دارند. ورودیهای لرزهای برای تحلیل سازهها، در حوزه زمان یا در حوزه بسامد و یا همزمان در هر دو حوزه زمان و بسامد گزارش میشوند. افزون بر این، شماری از سنجههای زمین لرزه به عنوان ورودی و برای تکمیل اطلاعات لازم برای انجام تحلیلهای گوناگون به کار میروند. بزرگا، شدت، بیشینه جا به جایی، سرعت، شتاب زمین، مدت (زمان تداوم)، بسامد غالب و … نمونههایی از این سنجهها هستند. همچنین، در برخی تحلیلها مانند تحلیل خطر پذیری لرزهای، برآورد آسیب سازهها، و تحلیل احتمالاتی لرزهای، پیش بینی شناسههای ورودی لرزهای مربوط به زلزلههای آینده ضروری است. این پیش بینیها به صورت معادلههایی تجربی ارائه میشوند. در این فصل، انواع مختلف ورودیهای لرزهای و شماری از رابطههای پیش بینی پر کاربرد، بررسی خواهند شد.
۳-۲- نگاشتهای تاریخچه زمانی
آشناترین شیوه برای نمایش جنبش زمین، نگاشت تاریخچه زمانی است. شناسه جنبش زمین میتواند شتاب، سرعت، جا به جایی و یا ترکیبی از این هر سه باشد. معمولاً شتاب مستقیماً اندازه گیری میشود و دیگر شناسهها از آن به دست میآیند. با این همه، جا به جایی و سرعت نیز میتوانند مستقیماً اندازه گیری شوند. نگاشتهای ثبت شده تاریخچه زمانی، ناگزیر همراه با خطاهایی هستند که از منابع گوناگونی چون نوفهها در بسامدهای بالا و پایین، خطای خط پایه، و خطاهای ابزاری و دستگاهی سرچشمه میگیرند. پیش از به کارگیری دادهها، این خطاها را حذف میکنند. همچنین، دادههای اندازه گیری شده به صورت پیوسته (قیاسی/آنالوگ) هستند که پیش از به کارگیری به عنوان ورودی لرزهای، میبایست گسسته و رقومی گردند. در سالهای اخیر، کاربرد لرزه نگارهای رقومی رواج بیشتری یافتهاند؛ با این حال، انواع خطاهای بر شمرده در بالا در هر دو گونه لرزه نگارهای پیوسته (قیاسی) و گسسته (رقومی) یافت میشوند. نگاشتهای تاریخچه زمانی جنبش زمین، مستقیماً در تحلیل قطعی سازهها در حوزه زمان به کار میروند.
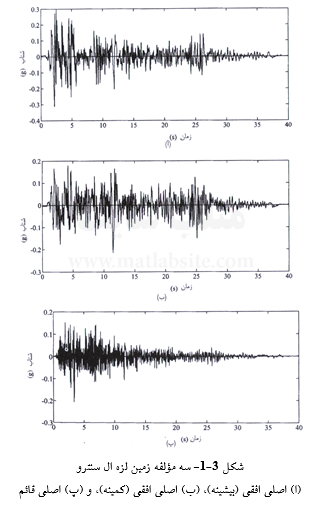
در هر ایستگاه سنجش، جنبش زمین در سه راستای عمود بر هم برداشت میشود: دو راستای افقی و یک راستای قائم. بدین ترتیب، سه مؤلفه جنبش زمین در هر ایستگاه در دسترس است. برای انجام تحلیل سازهها، این سه مؤلفه جنبش زمین به مؤلفههایی در راستاهای اصلی تبدیل میشوند. مشاهده شده است که راستای بیشینه جنبش زمین در امتداد خط واصل ایستگاه سنجش و رومرکز میباشد. بر این اساس، دو راستای اصلی دیگر نیز مشخص خواهند شد. مؤلفههای جنبش زمین در راستاهای اصلی نا همبسته آماریاند. در نتیجه، سه مؤلفه اصلی حرکت زمین را میتوان در جاهایی که نگاشتهای لرزهای در دسترس نیستند، به صورت مصنوعی نیز بازسازی کرد. در شکل ۲۳-۱ سه مؤلفه جنبش زمین در زلزله ال سنترو نشان داده شدهاند. نگاشتهای رقومی شده بسیاری از زمین لرزهها در تارنماهایی مانند www.peer.berkeley.edu/sncat در دسترس همگانیاند.
همان طور که در فصل ۲ گذشت، جنبش آزاد سطح زمین، نتیجه یک پدیده پیچیده در بردارنده بازتاب و شکست امواج و انتشار امواج سطحی،۵ و ترکیبی از امواج P، S و L است. بدین ترتیب، نگاشت امواج زمین که در ایستگاهای مکانی گوناگون برداشت میشوند، همسان نیستند؛ این ناهمسانی مکانی به صورت میدان همگن یا ناهمگن نمود مییابد. میدان همگن ناشی از یک جنبش یکسان است که با سرعت ثابت در زمین پیش میرود. در چنین میدانی، نگاشت های جنبش زمین در دو نقطه مکانی، تنها راای یک تأخیر زمانی هستند؛ اما، بیشینه یا rms (ریشه دوم میانگین مربعات) جنبش ها برای هر دو نقطه ایستگاهی یکسان است. در میدان ناهمگن جنبش زمین افزون بر تأخیر نگاشتها، بیشینه یا rms جنبش زمین در هر دو ایستگاه نیز متفاوت است. به سبب ناهمسانی جنبش زمین در نقاط گوناگون میدان، مؤلفههای دورانی و پیچشی جنبش زمین (حول محور قائم) پیدا میشوند. این مؤلفههای دورانی و پیچشی چنین به دست میآیند:
![]()
(۱-۳)
![]()
(۲-۳)
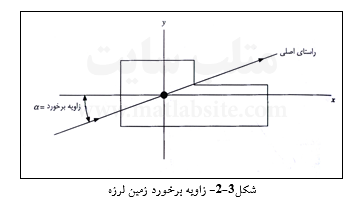
در این رابطهها، v,u و w جا به جایی زمین به ترتیب در راستاهای y, x و z میباشند؛ x و y دو مؤلفه افقی هستند که x راستای اصلی بیشینه است. چنانچه راستای اصلی بیشینه و محور اصلی بیشینه سازه همراستا نباشند، یک زاویه برخورد زلزله (a) نیز برای نگاشت لرزهای تعریف میشود.
بدین ترتیب، شناسایی کامل تاریخچه زمانی جنبش زمین در یک نقطه برای به کارگیری به عنوان ورودی لرزهای، نیازمند (u(t) ،![]() ،v(t) ،ω(t و (θ(t و مشتقهای زمانی آنهاست. افزون بر اینها، زاویه برخورد a نیز برای ساختمانهایی با پلان نامنظم، مانند شکل ۳-۲، ضروری میباشد.
،v(t) ،ω(t و (θ(t و مشتقهای زمانی آنهاست. افزون بر اینها، زاویه برخورد a نیز برای ساختمانهایی با پلان نامنظم، مانند شکل ۳-۲، ضروری میباشد.
۳-۳- محتوای بسامدی جنبش زمین
از آن جا که پاسخ سازه به نسبت میان بسامد طبیعی سازه به بسامد تحریک بستگی دارد، شناخت محتوای بسامدی جنبش زمین ضروری است. همچنین، برای انجام تحلیل سازه در حوزه بسامد (که در فصل سوم بدان پرداخته میشود)، ورودی لرزهای میباست محتوای بسامدی جنبش زمین باشد. بهترین و کاربردی ترین شیوه برای ساخت چنین ورودی لرزهای، استفاده از دنباله فوریه نگاشت زمانی جنبش زمین است. با فرض آن که این نگاشت، با دوره تناوبی برابر طول نگاشت پیوسته تکرار شود، میتوان آن را به صورت ترکیبی خطی از بیشمار تابعهای سینوسی و کسینوسی باز نوشت (این ترکیب خطی، به عنوان بسط دنباله فوریه تابع متناوب شناخته میشود):
![]()
(۳-۳)
در این رابطه، (x(t نگاشت تاریخچه زمانی (جا به جایی، سرعت یا شتاب)، ωn بسامد n ام، an و bn دامنههای توابع سینوسی و کسینوسی نظیر بسامد n ام و a0 دامنه نظیر بسامد صفر میباشند.
دامنههای an, a0 و bn با رابطههای زیر داده میشوند:
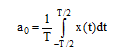
(۴-۳)
![]()
(۵-۳)
![]()
(۶-۳)
![]()
(۷-۳)
که T مدت زمان تداوم جنبش زمین (طول نگاشت) است.
دامنه فوریه نشان دهنده اندازه دامنه تابع سینوس یا کسینوس نظیر بسامد ωn است و با رابطه زیر به دست میآید:
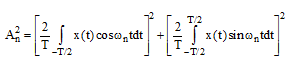
(۸-۳)
رابطه (۳-۳) را میتوان به نمایش زیر نیز در آورد:
![]()
(۹-۳)
که در آن، cn همان An است و ![]() چنین خواهد بود:
چنین خواهد بود:
![]()
(۱۰-۳)
نمودارهای cn و ![]() بر حسب بسامدهای ωn، به ترتیب طیف دامنه فوریه و طیف فاز فوریه خوانده میشوند.
بر حسب بسامدهای ωn، به ترتیب طیف دامنه فوریه و طیف فاز فوریه خوانده میشوند.
برای یافتن طیف دامنه فوریه یک نگاشت زمانی، میبایست انتگرالهای داده شده در رابطه ۳-۴ تا ۳-۶ محاسبه شوند. از آن جا که (x(t تابعی نامنظم از زمان است، انتگرالگیری با روشهای عددی انجام میپذیرد. این کار هم اکنون به سادگی، بر پایه تبدیل فوریه گسسته (DFT) و با الگوریتم FFT برنامه نویسی شده و در بیشتر نرم افزارهای ریاضیاتی و محاسباتی گنجانده شده است. در الگوریتم FFT، تجزیه فوریه یک نگاشت زمانی به کمک جفت انتگرالهای زیر در میدان مختلط (با استفاده از یک تابع نمایی مختلط) انجام میپذیرد:
![]()
(۱۱-۳)
![]()
(۱۲-۳)
انتگرال نخست، محتوای بسامدی نگاشت زمانی را در نمایش مختلط به دست میدهد، و دومین انتگرال، با داشتن محتوای بسامدی، نگاشت زمانی را بازیابی میکند. فرآیند دوم با الگوریتم IFFT (وارون تبدیل فوریه) انجام میگیرد.
ورودی FFT، نگاشت تاریخچه زمانی جنبش زمین میباشد که در بازههای زمانی گسسته نمونه برداری شده است. اگر N شمار برداشتهای نگاشت زمانی با گام زمانی Δt باشد که به عنوان ورودی به FFT داده میشوند، آن گاه N عدد مختلط به عنوان خروجی به دست میآید. N/2 عدد مختلط به دست آمده، محتوای بسامدی نگاشت زمانی را به دست میدهد که در آن، دامنه نظیر بسامد ωj برابر است با:
![]()
(۱۳-۳)
در این جا aj و bj به ترتیب بخشهای حقیقی و موهومی j امین عدید مختلط اند؛ فاز ![]() با رابطه زیر داده میشود:
با رابطه زیر داده میشود:
![]()
(۱۴-۳)
در این رابطه، بسامد jام برابر
![]()
میباشد که T طول نگاشت زمانی است.
![]()
بسامد نایکوئست نامیده میشود، و بسامدی است که پس از آن، مزدوجهای مختلط N/2 عدد مختلط نخست تکرار میشوند . تجزیه فوریه یک نگاشت گسسته زمانی را میتوان بر پایه الگوریتمهای FFT و IFFT، در نرم افزار Matlab به انجام رساند.
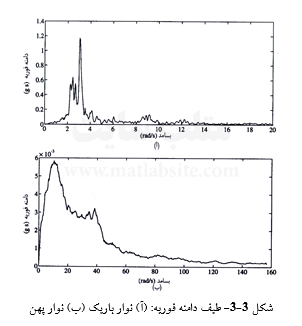
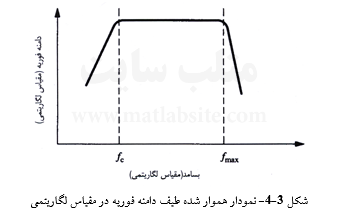
زلزله شناسان به منظور شناخت رفتار و ویژگیهای کلی و فراگیر طیفهای شتاب زمین، طیفهای شمار فراوانی از زمین لرزهها را ساخته، و پس از هموار سازی، بر روی نمودارهای لگاریتمی، مانند شکل ۳-۴ نمایش دادهاند. به خوبی میتوان دید که دامنههای شتاب فرویه در گسترهای میانی از بسامدها (با بسامد گوشه fc به عنوان کران پایین و بسامد جدایش به عنوان کران بالا) بیشینهاند. بررسی انجام گرفته بر روی دادههای زمین لرزهها نشان میدهند که fc با بزرگای زلزله نسبت عکس دارد.
مثال ۳-۱
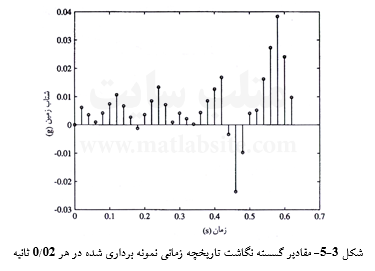
بخشی از یک نگاشت تاریخچه زمانی شتاب زمین که با گام زمانی s02/0=Δt نمونه برداری شده است، در زیر آمده است. (آ) دسته دادههای ورودی به FFT، (ب) دسته دادههای خروجی از FFT، و (پ) داده ورودی به IFFT را با نمودار نمایش دهید. همچنین، بسامد نایکوئست، طیف دامنه، و طیف فاز را بیابید. یادآوری میکند که به کارگیری چنین گستره کوچکی از نگاشت تاریخچه زمانی تنها ارزش آموزشی دارد.
پاسخ:
(آ) شکل ۳-۵، ۳۲ برداشت را از نگاشت زمانی شتاب زمین نشان میدهد که به عنوان ورودی به الگوریتم FFT نرم افزار Matlab داده میشوند:
![]()
در اینجا، y برداشتهای نگاشت تاریخچه زمانی است؛ YY نیز خروجی برداشتها با نمایش a+ib است (a بخش حقیقی؛ b بخش موهومی)
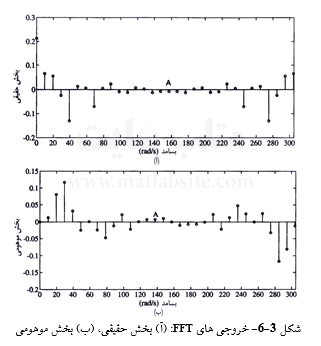
(ب) شکل ۳-۶- آ بخشهای حقیقی مقادیر خروجی را نشان میدهد. توجه کنید که نمودار نسبت به نقطه A متقارن است. آخرین مقدار در نیمه متقارن (نیمه دوم) کنار گذاشته شده است. این از آن روست که فرض شده است که برداشتها پس از (N(=32 بار، دوباره تکرار میشوند. شکل ۳-۶ ب بخشهای موهوی خروجیها را نشان میدهد. توجه کنید که نمودار نسبت به نقطه A پادمتقارن است. این نشان دهنده آن است که نیمه راست FFT دادههای ورودی، مزدوج مختلط نیمه چب میباشد.
(پ) بخشهای حقیقی و موهومی خروجیها در کنار هم و در نمایش مختلط a+ib نوشته میشوند. بدین ترتیب، ۳۲ نقطه داده با این نمایش در دسترسند. همان گونه که پیشتر گفته شد، نیمه راست دادهها مزدوج مختلط نیمه چپ هستند. این دادههای مختلط ورودی IFFT را میسازند. خروجی IFFT همان ۳۲ مقدار برداشت شده نمودار تاریخچه زمانی نشان داده شده در شکل ۲-۵ است. شایان توجه است که اگر ورودیهای IFFT مزدوج مختلط یکدیگر نبودند،
خروجیهای IFFT نیز مقادیر حقیقی نمیشدند. این نکته بسیار با اهمیت است و در تحلیل لرزهای سازهها در حوزه بسامد با FFT به کار خواهد آمد.
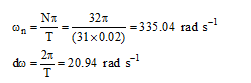
طیف دامنه فوریه، نمودار
![]()
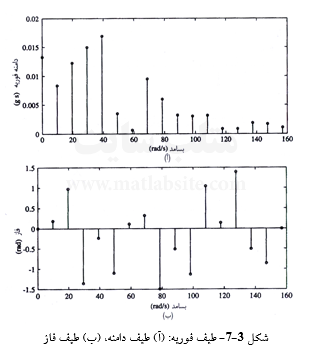
بر حسب (ωi(0-dω-ωn است. برای یافتنai, ، خروجیهای FFT نرم افزار MATLAB را میبایست بر N/2 تقسیم کرد. نمودار طیف دامنه در شکل ۳-۷- آ نشان داده شده است. طیف فاز نیز نمودار (tan-1(bi/ai بر حسب ωi میباشد که در شکل ۳-۷- ب نمایش داده شده است.
۴-۳- تابع چگالی طیفی توان جنبش زمین
محتوای بسامدی جنبش زمین را میتوان با طیف توان یا چگالی طیفی توان نیز نشان داد. تفاوت میان محتوای بسامد نمایش داده شده با طیف توان و طیف دامنه فوریه در آن است که اولی، برآوردی احتمالاتی را از محتوای بسامدی جنبشهای پیش رو ساختگاه به دست میدهد؛ جنبشهایی که هنوز رخ ندادهاند. از آن سو طیف دامنه فوریه محتوای بسامدی یک جنبش رخ داده را در ساختگاه گزارش میکند (مگر در آن جا که داده زمین لرزه در دسترس نباشد و به کمک یک رابطه تجربی پیش بیی شود.)
از آن جا که زلزلههای آینده ناشناختهاند، بهره گیری از یک الگوی احتمالاتی برای ورودیهای لرزهای منطقی به نظر میرسد. رایجترین شیوه برای نمایش ورودیهای لرزهای به روش احتمالاتی، معرفی اندازه محتمل میانگین مربعات یا بیشینه شتاب زمین برای زلزله آینده در ساختگاه است. با این حال، در تحلیل سازهها به شیوه های دینامیکی احتمالاتی، تابع چگالی طیفی توان شتاب زمین (تابع توزیع میانگین مربعات شتاب بر حسب بسامد)، ورودی بهتری است. برای بیان تابع چگالی طیفی توان، زمین لرزههای آینده را میبایست فرآیندهای تصادفی مانا انگاشت.
چگونگی یافتن تابع چگالی طیفی توان (PSDF) یک فرآیند تصادفی مانا نیازمند آشنایی با دانش فرآیندهای تصادفی یا ارتعاشهای تصادفی است که کتابهایی چند بدان پرداختهاند. با فرض ارگودیک بودن فرآیند تصادفی، که بر پایه آن میتوان از هر تاریخچه زمانی دلخواه از فرآیند تصادفی, ویژگیهای آماری مرتبه دو آن را به دست آورد، PSDF فرآیند به کمک دنباله فوریه پیدا میشود. در بسیاری از حلهای کاربردی، فرآیند تصادفی مانا، ارگودیک نیز انگاشته میشود.
میانگین مربعات نگاشت تاریخچه زمانی با مدت زمان T چنین محاسبه میشود.
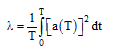
(۱۵-۳)
با بهره گیری از قضیه پارسوال، میتوان λ را چنین نوشت:
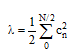
(۱۶-۳)
که Cn اندازه مطلق دامنه مختلط (رابطه ۳-۹) در بسامد ω است که از FFT به میآید.
تابع چگالی طیفی توان (S(ω به گونه ای تعریف میشود که:
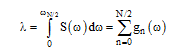
(۱۷-۳)
باشد. از مقایسه دو رابطه (۳-۱۶) و (۳-۱۷) به دست میآید:
![]()
(۱۸-۳)
که در آن، g(ω)=S(ω)dω است و عملگر انتگرال گیری با عملگر برهم نهی اندازههای گسسته (Σ) جایگزین میشود.
از رابطه (۳-۱۸) پیوند نزدیک میان طیف توان و طیف دامنه فوریه برای یک فرآیند ارگودیک به روشنی آشکار میشود. بر پایه رابطه (۳-۱۷)، تابع چگالی طیف توان یک فرآیند تصادفی مانا را میتوان برابر توزیع میانگین مربعات آن (که یکتا و ناوردای زمانی است) بر حسب بسامد دانست.
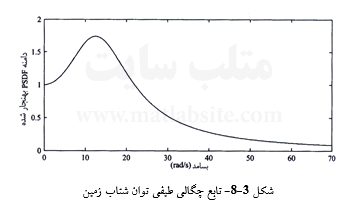
در شکل ۳-۸، یک نمونه PSDF شتاب زمین نشان داده شده است. شماری از سنجههای مهم جنبش زمین با گشتاورهای PSDF رابطه دارند. گشتاور n ام PSDF چنین میباشد.
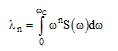
(۱۹-۳- آ)
که ωc بسامد جدایش PSDF است؛ بسامدی که پس از آن، بخش پایانی نمودار PSDF بریده میشود. λ۰ میانگین مربعات شتاب زمین میباشد. شناسهای به نام بسامد مرکزی به صورت زیر تعریف میشود:
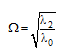
(۱۹-۳- ب)
Ω بسامدی است که PSDF در آن تمرکز یافته است. با استفاده از λ۰Ω و مدت زمان زمین لرزه، Td، میانگین شتاب بیشینه زمین (PGA) را میتوان چنین به دست آورد:
![]() (۱۹-۳- پ)
(۱۹-۳- پ)
یک شناسه خوب برای نمایش محتوای بسامدی شتاب زمین، بسامد یا دوره تناوب غالب است، که برابر با دوره تناوب نظیر بیشینه دامنه طیف فوریه یا بسامد نظیر بیشینه PSDF میباشد.
برای یافتن پاسخ سازههای با چند تکیه گاه، که در برابر تحریکهایی نا همسان قرار دارند، به کارگیری PSDF تحریکها در تحلیل، به تنهایی کافی نیست، و نیاز به ورودی دیگری است که نبود همبستگی میان هر دو تحریک را نشان دهد. نبود این همبستگی با تابع دگر همبستگی (همبستگی دو به دو یا متقابل) یا تابع چگالی طیفی توان دو به دو نمایش مییابد، که دومی در تحلیل حوزه بسامد کاربرد دارد. تابع چگالی طیفی توان دو به دو برای دو تابع تحریک x1 و x2 (که فرآیندهای تصادفی مانا انگاشته میشوند) به صورت زیر است:
![]()
(۲۰-۳)
که (Sx1(ω و Sx2(ω) PSDFهای x1 و x2 هستند و (coh(x1, x2, ω تابع همدوسی میباشد که ناهمبستگی میان x1 و x2 را نشان میدهد.
در یک میدان تحریک همگن با یک موج زلزله گذرای همسان در همه نقاط، PSDF شتاب زمین در تکیه گاههای مختلف یکسان است، اما به سبب تأخیر زمانی، میان هر دو تکیه گاه ناهمبستگی دیده میشود. در چنین حالتی، تابع چگالی طیفی توان دو به دو بین هر دو تحریک خواهد بود:
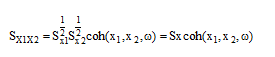
(۲۱-۳)
که Sx(ω)، PSDF نگاشت شتاب زمین است.
نگاشتهای مربوط به جنبشهای نیرومند زمین نشان میدهند که الگوسازی زمین لرزه به صورت یک فرآیند تصادفی مانا چندان مناسب نیست، چرا که میانگین دسته مربعات آنها با زمان تغییر میکند. همانطور که در شکل ۳-۹ نشان داده شده است، این میانگین مربعات به آرامی تا مقداری بیشینه بالا میرود، سپس در یک دوره زمانی ثابت میماند، و آنگاه دوباره کاهش مییابد. چنین فرآیندی با تابع چگالی طیفی توان تکاملی (وردای زمانی) نمایش داده میشود. طیف وردای زمانی از ضرب یک طیف ثابت در یک تابع تعدیل زمانی، همانند زیر، به دست میآید:
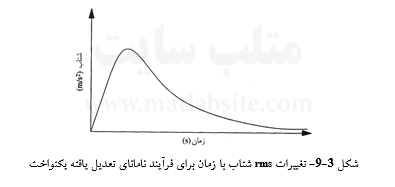
(S(ω,t)=|q(t)|2S(ω
(۲۲-۳)
پژوهشگران، با پردازش دستههای گوناگون نگاشتهای زمین لرزه، چندین گونه تابع چگالی طیفی توان، تابعهای تعدیل و تابعهای همبستگی را پیشنهاد کردهاند، که در بخشهای ۳-۷-۵ و ۳-۷-۶ گزارش خواهند شد.
مثال ۳-۲
با فرض آن که تکه نگاشت تاریخچه زمانی مثال ۳-۱ نشانگر یک فرآیند ارگودیک باشد، PSDF آن را به دست آورید.
پاسخ:
با بهره گیری از معادله های ۳-۹، ۳-۱۶ و ۳-۱۸، برابر زیر به دست میآید:
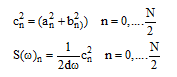
مقادیر ![]() با مربع گیری از دامنههای طیف فوریه به دست میآیند. نمودارهای (S(ω بر حسب PSDF) ω) در شکل ۳-۱۰ و ۳-۱۱ نشان داده شدهاند. توجه نمایید که پهنای بازهها در شکل ۳-۱۰ برای T های بزرگتر، باریکتر میشود.
با مربع گیری از دامنههای طیف فوریه به دست میآیند. نمودارهای (S(ω بر حسب PSDF) ω) در شکل ۳-۱۰ و ۳-۱۱ نشان داده شدهاند. توجه نمایید که پهنای بازهها در شکل ۳-۱۰ برای T های بزرگتر، باریکتر میشود.
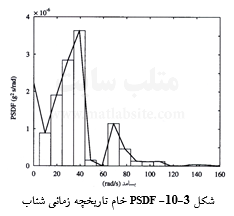
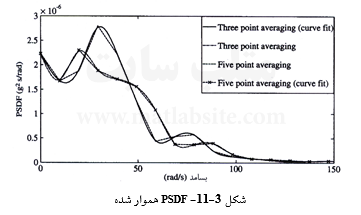
طیف نشان داده شده در شکل ۳-۱۰ بسیار نامنظم است. معمولاً چنین طیفهای نامنظمی را با روشهای هموارسازی طیفی هموار میکنند. در اینجا، با یک روش هموارسازی ۵ نقطه ای، طیف هموار شکل ۳-۱۱ به دست میآید. برای هموار سازی، اندازه دامنه طیف در هر نقطه، با میانگین اندازه دامنههای ۵ نقطه از طیف (همان نقطه و دو نقطه پیرامونی در هر دو سوی آن) جایگزین میشود. نقطههای نزدیک به آغاز و پایان طیف با شمار کمتری نقطه میانگین یابی میشوند. برای نمونه، نقطه یکم طیف، با دامنههای نقطههای یکم، دوم و سوم میانگین گیری میشود؛ نقطه دوم با دامنههای نقطههای یکم، دوم، سوم و چهارم، نقطه ۱۶ ام با دامنههای نقطههای ۱۷ ام، ۱۶ ام، ۱۵ ام و ۱۴ ام، و به همین ترتیب. چنانچه شمار نقطهها زیاد باشد، میانگین گیری با نقاط بیشتر امکان پذیر است، و PSDF هموارتری را به دست میدهد. در صورت لزوم، با برازش یک تابع چند جملهای میتوان طیف بسیار همواری را همانند شکل ۳-۱۱ به دست آورد. برای این مسأله:
مجموع سطوح میلهها برابر است با:
۰٫۰۱۱(ms-2)2
سطح زیر PSDF هموار شده برابر است با:
۰٫۰۱۱۳(ms-2)2
سطح زیر نمودار چند جملهای برازش شده برابر است با:
۰٫۰۱۱۲ (ms-2)2
میانگین مربعات تاریخچه زمانی برابر است با:
۰٫۰۱۲ (ms-2)2
میباشند.
۵-۳- طیف پاسخ زمین لرزه
سومین گونه طیفی که میتوان از آن به عنوان ورودی لرزهای بهره جست، طیف پاسخ زمین لرزه است. طیف پاسخ زمین لرزه بهترین ورودی لرزهای برای مهندسان زلزله به شمار میآید. چندین نوع طیف پاسخ برای نمایش جنبش زمین پیشنهاد شدهاند که طیف پاسخ جا به جایی، طیف پاسخ شبه سرعت، طیف پاسخ شتاب مطلق، و طیف انرژی از آن میانند. این طیفها میتوانند محتوای بسامدی جنبش زمین را، البته نه به گونهای مستقیم (آن گونه که طیف فوریه بیان میکرد) نشان دهند. طیف پاسخ شتاب مطلق کاربردیترین ورودی برای تحلیل لرزهای سازهها با روش طیفی است.
۱-۵-۳- طیفهای جا به جایی، سرعت و شتاب
با یافتن طیف پاسخ جا به جایی، میتوان به دیگر طیفها نیز دست یافت. بنا به تعریف، طیف پاسخ جا به جایی، نمودار بیشینه جا به جایی سامانه یک درجه آزادی (SDOF) در برابر جنبش دلخواه زمین است که به صورت تابعی از بسامد طبیعی و نسبت میرایی SDOF بیان میشود.
جابه جایی نسبی سامانه SDOF نسبت به تکیه گاه آن در هر لحظه زمانی t در اثر شتاب پایه و با شرایط اولیه
![]()
برابر است با:
![]()
(۲۳-۳)
بیشینه (x(t را میتوان چنین نوشت:
![]()
(۲۴-۳- آ)
که Sv برابر است با:
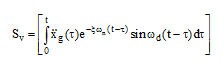
(۲۴-۳- ب)
در بیشینه جا به جایی، انرژی جنبشی KE=0 میباشد. از این رو، انرژی کل سامانه خواهد بود.
![]()
(۲۵-۳- آ)
اگر این انرژی در نمایش انرژی جنبشی باز نویسی شود، سرعت معادل سامانه برابر میشود با:
![]()
(۲۵-۳- ب)
که به دست میدهد:
![]()
(۲۵-۳- پ)
با نگاه به دو رابطه (۳-۲۴- آ) و (۳-۲۵- ب) میتوان دریافت که است. در مهندسی زلزله، این سرعت را با نام شبه سرعت طیفی میشناسند که متفاوت از بیشینه سرعت واقعی سامانه است.
برای هر زمین لرزه دلخواه، نمودارهای Sd و Sv که برای گستره کاملی از بسامدهای SDOF و با انگاشت نسبت میرایی دلخواه به دست میآیند، به ترتیب طیف پاسخ جا به جایی و طیف پاسخ شبه سرعت خوانده میشوند. سنجه دیگری که به خوبی بیانگر پاسخ SDOF به جنبش زمین میباشد، شتاب (یا شبه شتاب) طیفی است که چنین تعریف میشود:
![]()
(۲۶-۳)
نمودار Sa برای گستره کاملی از بسامدهای SDOF و با نسبت میرایی دلخواه، طیف پاسخ شتاب نامیده میشود، و برای یافتن بیشینه نیروی زمین لرزه وارد بر سازه به کار میرود. برای یک سامانه SDOF، بیشینه نیروی پدید آمده در فنر SDOF برابر است با:
![]()
(۲۷-۳)
بر پایه رابطه ۳-۲۷، حاصل ضرب جرم SDOF در شتاب طیفی، بیشینه نیروی سامانه را ناشی از زلزله به دست میدهد. به همین خاطر، شتاب طیفی، برابر رابطه ۳-۲۶ و متفاوت از شتاب بیشینه سامانه تعریف شده است. پس، هر چند طیف پاسخ جا به جایی، نمودار جا به جایی بیشینه سامانه به صورت تابعی از بسامد است، طیفهای شبه شتاب و شبه سرعت، نمودارهای بیشینه سرعت SDOF نمیباشند.
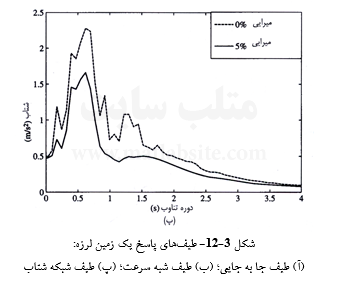
این سه طیف، که نمونههایی از آنها در شکلهای ۳-۱۲- (آ – پ) نشان داده شدهاند، چندین شناسه و سنجه فیزیکی دیگر را نیز میتوانند ارزیابی کنند. طیف جا به جایی آشکارا با بیشینه جا به جایی سامانه SDOF ارتباط دارد. طیف شبه سرعت به بیشینه انرژی کرنشی انباشته در سامانه در مدت زمان رخداد زمین لرزه، رابطه ۳-۲۵- آ، ارتباط مییابد. طیف شبه شتاب نیز به بیشینه نیروی لرزهای پدید آمده در سامانه، رابطه ۳-۲۷، مربوط میشود.
۲-۵-۳- طیف انرژی و طیف فوریه
نمایشی دیگری برای جنبش زمین، طیف پاسخ انرژی بیشینه است. این طیف با رسم نمودار 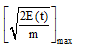 برای گستره کاملی از بسامدهای (دوره تناوب) سامانه SDOF و برای یک میرایی دلخواه به دست میآید. انرژی (E(t سامانه SDOF در لحظه زمانی t برابر است با:
برای گستره کاملی از بسامدهای (دوره تناوب) سامانه SDOF و برای یک میرایی دلخواه به دست میآید. انرژی (E(t سامانه SDOF در لحظه زمانی t برابر است با:
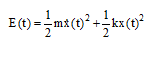
(۲۸-۳)
بنابراین، 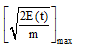 خواهد شد:
خواهد شد:
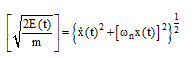
(۲۹-۳)
این بیشینه را میتوان برای هر بسامد (یا دوره تناوب) سامانه SDOF و برای میرایی دلخواه به دست آورد.
برای ![]() ، از رابطههای ۳-۲۹ و ۳-۲۳ به آسانی میتوان نشان داد که:
، از رابطههای ۳-۲۹ و ۳-۲۳ به آسانی میتوان نشان داد که:
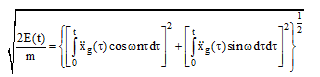
(۳۰-۳)
با نگاه به رابطههای ۳-۸ و ۳-۳۰ آشکار میشود که طیف دامنه فوریه و طیف پاسخ انرژی نمایشی همسان دارند. یادآوری میکند که (x(t در رابطه ۳-۸ میتواند هر شناسهای از جنبش زمین همچون
![]()
باشد. طیف دامنه فوریه را میتوان برآوردی از انرژی کل سامانه نامیرای SDOF در پایان زمان t (یعنی t=T) دانست. طیف انرژی بیشینه عموماً بزرگتر از طیف دامنه فوریه است، چرا که انرژی بیشینه در زمانی پیش از پایان زلزله رخ میدهد.
مثال ۳-۳
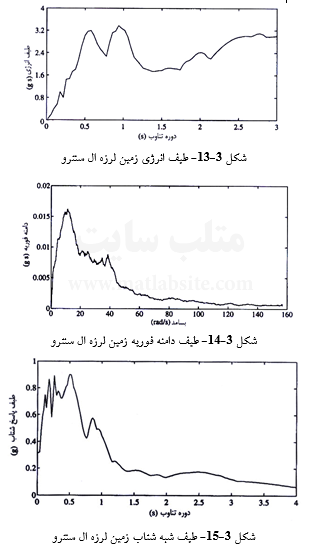
طیف انرژی بیشینه، طیف فوریه هموار شده، و طیف شبه شتاب را (به ازای ) برای نگاشت زمین لرزه ال سنترو با یکدیگر بسنجید. همچنین، دورههای تناوب نظیر بیشینههای این سه طیف را بیابید و با هم مقایسه کنید.
پاسخ:
در شکلهای ۳-۱۳ تا ۳-۱۵، طیف انرژی، طیف فوریه و طیف شبه شتاب برای نگاشت زمین لرزه ال سنترو نمایش داده شدهاند. این طیفها از رابطههای ۳-۲۰ تا ۳-۲۲ و ۳-۱۳ به دست آمده اند. به کمک نرم افزار MATLAB، میتوان برنامههایی ساده را برای یافتن این طیفها نوشت. همچنین میتوان از نرم افزار (www.seismosoft.com) Seismo signal برای یافتن طیفهای فوریه و شبه شتاب بهره جست. طیف انرژی را نیز میتوان با استفاده از رابطه ۳-۲۹ و نتایج seismo signal به دست آورد.
s0/95 = بیشینه دوم ؛ s0/55 = بیشینه یکم ؛ (طیف انرژی) (بیشینه) T
s0/85 = (طیف فوریه) (بیشینه) T
s0/51 = (طیف شبه شتاب) (بیشینه) T
ملاحظه میشود که بیشینههای هر سه طیف تقریباً در یک زمان رخ میدهند. این نشان دهنده آن است که بسامد یا دوره تناوبی را که بیشینه انرژی زمین لرزه در آن رخ میدهد، به آسانی میتوان از هر یک از سه طیف بالا برآورد کرد.
۳-۵-۳- طیف ترکیبی D-V-A
سه طیف جا به جایی، شبه سرعت و شبه شتاب، هر یک به گونهای، اطلاعای یکسان را درباره پاسخ سازه به دست میدهند. با این حال، همان طور که پیشتر نیز گذشت، هر کدام از آنها یک شناسه فیزیکی معنادار را ارزیابی میکنند. بنابراین، هر سه طیف در فهم طبیعت زمین لرزه و نیز طراحی مقاوم لرزهای، سودمند و با ارزشند. مهمتر آن که هر سه طیف، در تعریف و ساخت طیف پاسخ طرح، که در آینده بدان پرداخته خواهد شد، به کار میآیند. از این رو، دستیابی به یک نمودار ترکیبی که هر سه شناسه طیفی را یک جا نمایش دهد، بسیار ارزشمند خواهد بود. دستیابی به چنین نمایش یکپارچهای، با توجه به رابطه میان این سه شناسه طیفی، شدنی و امکان پذیر است.
با لگاریتم گیری از رابطههای ۳-۲۴- آ و ۳-۲۶ به دست میآید که:
![]()
(۳۱-۳)
![]()
(۳۲-۳)
نمایش این دو رابطه بر روی نمودار لگاریتمی با محور قائم logSv و محور افقی logωn ، و به ازای logSd و logSa ثابت، به ترتیب خطهایی با شیب ۴۵º + و ۴۵º – را به دست میدهد.
چنانچه به جای logωn، لگاریتم دوره تناوب (T(2π/ωn در نظر گرفته شود، این خطهای راست عمود بر هم، با یکدیگر جا به جا خواهند شد. بدین گونه میتوان هر سه طیف را به مانند شکل ۳-۱۶، بر روی یک نمودار لگاریتمی با چهار محور (نمودار چهار محوره یا نمودار سه جانبه) رسم نمود.
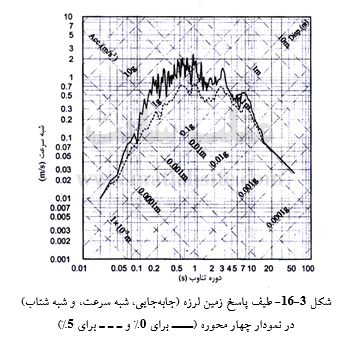
چنانچه تنها با جفت داده های logSv و logT، طیف شبه سرعت بر روی این نمودار رسم شود، میتوان اندازههای logSv و logSd را برای T دلخواه، از همان نمودار بازخوانی کرد. برای رسم نمودار، چند شرط محدود کننده را میبایست منظور نمود، چرا که نمایش مقادیر logT برای T→۰ و T→∞ شدنی نیست. شرطهای محدود کننده زیر در رسم نمودار به کار میآیند:
![]()
(۳۳-۳)
![]()
(۳۴-۳)
دو شرط محدود کننده بالا را میتوان با استنتاج فیزیکی دریافت. برای یک سامانه با دوره تناوب بسیار طولانی (∞→T)، که نشان دهنده یک سامانه بسیار منعطف و نرم است، انتظار میرود که جرم به هنگام جا به جایی زمین، ثابت بماند؛ در نتیجه ![]() و
و ![]() خواهد شد. برای یک سازه با دوره تناوب بسیار کوتاه، جرم همراه با تکیه گاه به صورت صلب جا به جا میشود، و شتاب بیشینه آن همانند تکیه گاه خواهد بود. در نتیجه،
خواهد شد. برای یک سازه با دوره تناوب بسیار کوتاه، جرم همراه با تکیه گاه به صورت صلب جا به جا میشود، و شتاب بیشینه آن همانند تکیه گاه خواهد بود. در نتیجه،
![]()
میشود. از آن جا که ![]() (فصل سوم) است،
(فصل سوم) است، ![]() میباشد.
میباشد.
شکل ۳-۱۷ طیف پاسخ را با میرایی ۵% برای زلزله ال سنترو نشان میدهد. در این شکل، طیف پاسخ با یک دسته خط های راست، یکدست و هموار شده است. از روی شکل میتوان دید که خط راست زیر نقطه a و خط راست بین نقطه های b و c، موازی محور Sd/ugmax هستند. خط زیر نقطه a نشان دهنده Sa ثابت برابر با ![]() است. خط بین Sd/ugmax هستند. خط زیر نقطه a نشان دهنده Sa ثابت برابر با
است. خط بین Sd/ugmax هستند. خط زیر نقطه a نشان دهنده Sa ثابت برابر با ![]() است. خط بین نقطههای b و c نیز شتاب ثابتی را برابر با ضریبی از
است. خط بین نقطههای b و c نیز شتاب ثابتی را برابر با ضریبی از ![]() نشان میدهد.
نشان میدهد.
بدین ترتیب، بخش سمت چپ نقطه c از طیف پاسخ با بیشینه شتاب زمین ارتباط پیدا میکند. به همین گونه، بخش سمت راست d از طیف پاسخ به بیشینه جا به جایی زمین ارتباط می یابد. بخش میانی c-d نیز به بیشینه سرعت جنبش زمین بستی دارد.
طیفهای پاسخ زمین لرزه گوناگون، همگی از همین الگوی ساختاری پیروی میکنند؛ با این همه، نقطه های f, e, d, c, b, a و دوره های تناوب همتای آنها Ta, Tb, Tc, Td, Te و Tf برای زمین لرزهها و نسبت میرایی گوناگون تغییر میکنند.
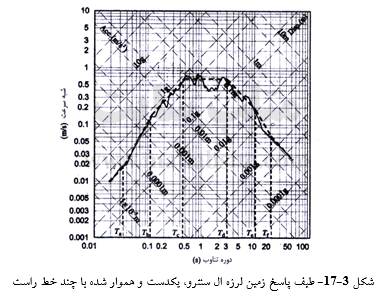
بر پایه این یافتهها، منطقی است که طیف را به سه ناحیه: ناحیه حساس به جا به جایی (ناحیه با دوره تناوب زیاد)، ناحیه حساس به شتاب (ناحیه با دوره تناوب کم)، و ناحیه حساس به سرعت (ناحیه با دوره تناوب متوسط) تقسیم کرد. همه زمین لرزههای ثبت شده در شرایط همسان و ناهمسان، الگوی همانندی را برای طیف پاسخ در هر یک از این سه ناحیه به دست میدهند. از شکل ۳-۱۶ آشکار است که بیشترین تأثیر میرایی به طیف پاسخ، در ناحیه حساس به سرعت، و کمترین تأثیر آن نیز در ناحیههای حساس به شتاب و جا به جایی است.
یک دست و هموار کردن طیف با یک دست خط راست، شیوه چندان دقیقی برای تعریف طیف به شمار نمیآید. این شیوه و یا هر شیوه دیگر برازشی را نمیتوان جایگزینی منطقی برای نمایش طیف پاسخ واقعی دانست. با این همه، در بخش آینده خواهد آمد که این کار، در ساخت طیف طرح که در طراحی لرزهای سازهها بیش از طیف پاسخ یک زمین لرزه مشخص به کار میآید، سودمند خواهد بود.
مثال ۳-۴
طیف پاسخ شتاب زمین را برای زلزله پارک فیلد به ازای ![]() رسم کنید. پس از یکدست کردن نمودار با یک دسته خط راست، Ta, Tb, Tc, Td, Te و Tf را بیابید و با مقدارهای به دست آمده برای زلزله ال سنترو مقایسه کنید.
رسم کنید. پس از یکدست کردن نمودار با یک دسته خط راست، Ta, Tb, Tc, Td, Te و Tf را بیابید و با مقدارهای به دست آمده برای زلزله ال سنترو مقایسه کنید.
پاسخ:
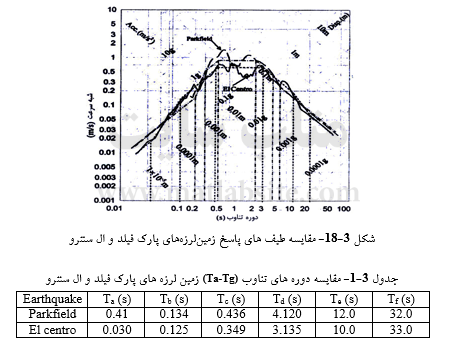
نگاشت تاریخچه زمانی (رقومی شده) شتاب زمین لرزه پارک فیلد از تارنمای www.peer.berkley.edu/smact در دسترس است. طیفهای جابهجایی، شبه سرعت و شبه شتاب از رابطههای ۳-۲۳ تا ۳-۲۶ به دست میآیند. همچنین میتوان همانند مثال ۳-۳، از نرم¬افزار seismo signal نیز بهره جست. سپس طیفها بر روی نمودار چهار محوره رسم، و آن گونه که در شکل ۳-۱۸ نشان داده شده است، با یک دسته خط راست، یکدست و هموار میشوند.
در جدول ۳-۱ مقدار Ta, Tb, Tc, Td, Te و Tf به دست آمده از نمودار، با مقدارهای نظیر در زلزله ال سنترو مقایسه شدهاند.
۴-۵-۳- طیف پاسخ طرح و ساخت آن
طیف پاسخ طرح (یا طیف پاسخ طراحی) با طیف ساده پاسخ یک زمین لرزه متفاوت است. این طیف، از آن رو که برای طراحی سازههای جدید یا برآورد خطر پذیری (ریسک) سازههای موجود در برابر زلزلههای آینده (که البته ناشناخته و نامعلومند) به کار میرود، میبایست الزاماتی را برآورده سازد. این الزامات عبارتند از:
آ) طیف طرح باید تا آن جا که شدنی است، هموار و بدون آشفتگیهایی باشد که در طیف پاسخ یک زمین لرزه، مانند شکل ۳-۱۶، به چشم میخورد. این الزام به دو دلیل ضروری است: نخست آن که آشفتگیها در طیفهای دو زمین لرزه مختلف میتوانند بسیار متفاوت از یکدیگر باشند، و در نتیجه برآورد نادرستی را از دامنههای طیفی برای زلزله های آینده به دست دهند. دوم آن که برای یک طیف بسیار آشفته دامنههای طیفی ممکن است به ازای تغییری کوچک در بسامد، به شدت تغییر کنند. از آن که همواره مقداری عدم قطعیت در تعیین بسامدهای طبیعی سازهها وجود دارد، یک طیف آشفته ممکن است برآورد بسیار نادرستی را از نیروهای زلزله به دست دهد. از همین رو، انـتظار آن است که طیف طرح در نمودار لگاریتمی چهار محوره، در بردارنده یک دسته خط راست، همانند شکل ۳-۱۷، باشد.
ب) طیف طرح میبایست نماینده طیفهای جنبش زمین برای زلزلههای گذشته منطقه باشد. چنانچه برای منطقه مورد بررسی، هیچ نگاشت زلزلهای ثبت نشده باشد، و یا نگاشتهای زلزله به شمار کافی در دسترس نباشند، میتوان از نگاشتهای ساختگاههای دیگر با شرایط همسان بهره جست. این شرایط همسان در بردارنده عواملی چون بزرگای زلزله، فاصله ساختگاه از گسل، ساز و کار گسل، ویژگیهای زمین شناختی مسیر گذر امواج لرزهای از چشمه تا ساختگاه، و شرایط محلی خاک محل ساختگاه هستند.
پ) یک طیف پاسخ تک، به تنهایی نمیتواند نشان دهنده همه تغییرات در طیفهای زمین لرزههای گذشته منطقه باشد. از این رو، معمولاً دو طیف پاسخ به عنوان طیف طرح گزارش میشوند، یک طیف میانگین (با احتمال فراگذشت ۵۰%) و یک طیف میانگین به علاوه انحراف معیار (با احتمال فراگذشت ۸۴%)
ت) طیف پاسخ طرح میبایست نسبت به بیشینه شتاب زمین (PGA) بهنجار (هم پایه) شود، چرا که PGA از ساختگاهی به ساختگاه دیگر بسیار متفاوت است. افزون بر این، طیف پاسخ طرح میبایست با اندازه نیروهای زلزله یا میزان تغییر شکل سازهها در زمین لرزههای گذشته سازگاری داشته باشد.
ث) در پایان آن که طیف پاسخ طرح باید با فلسفه طراحی لرزهای هماهنگ باشد. امروزه، یک فلسفه طراحی دو گانه (دو معیاری / دو ترازه) کاربرد یافته است (در آینده بررسی خواهد شد)، که بر پایه آن، به دو طیف طرح، یکی برای طراحی و دیگری برای برآورد ایمنی رخدادهای حدی، نیاز میباشد. عموماً ساختار شکلی دو طیف باید یکسان در نظر گرفته شوند.
با در نظر گرفتن الزامات بالا و ویژگیهای طیف یک دست شده پاسخ که پیشتر بدان پرداخته شد، فرآیندی برای ساخت طیف پاسخ طرح پیشنهاد شده است. این فرآیند در بردارنده گامهای زیر است:
۱٫ مقادیر PGA مورد انتظار در منطقه برای زلزلههای محتمل بیشینه و طرح، با انجام تحلیل خطر، که در فصل گذشته بدان پرداخته شد، به دست میآیند.
۲٫ مقادیر بیشینه سرعت و جا به جایی زمین، از رابطههای تجربی معتبر برای منطقه برآورد میشوند. این رابطهها دارای نمایش فراگیر زیر هستند:
![]()
مقادیر c1 و c2 از دادههای ثبت شده زمین لرزه پیدا میشوند، که میتوان آنها را برابر c1=1/22~0/9 ms-1 و ۶=c2 در نظر گرفت.
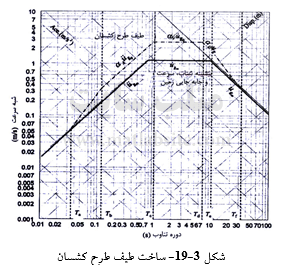
۳٫ بر روی کاغذ لگاریتمی چهار محوره، خطهای پایه نمایش دهنده ![]() آن گونه که در شکل ۳-۱۹ نشان داده شده است، رسم میشوند. از ضرب
آن گونه که در شکل ۳-۱۹ نشان داده شده است، رسم میشوند. از ضرب ![]() به ترتیب در ضریبهای بزرگنمایی
به ترتیب در ضریبهای بزرگنمایی![]() خطهای de, bc و cd به دست میآیند.
خطهای de, bc و cd به دست میآیند.
۴٫ توجه داشته باشید که نقطههای c و d که محل برخورد شاخههای A ثابت، V ثابت و D ثابت هستند، از ضریب های ![]() به دست میآیند. مقادیر
به دست میآیند. مقادیر ![]() ، همان طور که انتظار میرود، به میرایی وابسته هستند. از همین رو، محل این نقطههای برخورد یعنی c و d به میرایی بستگی دارند. مقادیر ، و از دادههای ثبت شده زمین لرزه به دست میآیند. اندازههایی برای ، و پیشنهاد شدهاند. این اندازهها از پردازش شمار فراوانی دادههای لرزهای به دست آمدهاند.
، همان طور که انتظار میرود، به میرایی وابسته هستند. از همین رو، محل این نقطههای برخورد یعنی c و d به میرایی بستگی دارند. مقادیر ، و از دادههای ثبت شده زمین لرزه به دست میآیند. اندازههایی برای ، و پیشنهاد شدهاند. این اندازهها از پردازش شمار فراوانی دادههای لرزهای به دست آمدهاند.
۵٫ دورههای تناوب متناظر با نقاط e، b، a و f روی نمودار ثابت هستند، و مقادیر دقیق آنها به دادههای ثبت شده در منطقه بستگی دارند. با فرض یک بسامد f1، معمولاً نقطه b دارای بسامد در حدود fb=4f1 و نقطه a دارای بسامد در حدود fa=10f1 میباشند. نقطههای e و f دارای بسامدهای بسیار پایین (دورههای تناوب بالا) و به ترتیب در حدود (۱/۱۵~۱۰-۱) و (۱/۳۵~۱/۳۰) میباشند. برای کامل شدن طیف، a به b و e به f وصل میشود.
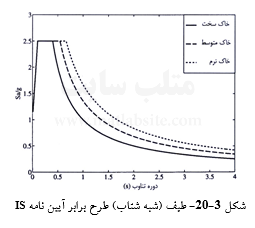
۶٫ هنگامی که طیف طرح در یک نمودار لگاریتمی چهار محوره رسم گردید، میتوان طیف پاسخ شتاب بهنجار را از آن بازیابی، و در نمایش معمول (نمودار دو محوره) ترسیم کرد. شکل ۳-۲۰، یک نمونه نمودار طیف شبه شتاب بهنجار (به دست آمده از یک نمودار لگاریتمی) را نشان میدهد. در آیین نامهها، طیف شتاب، این گونه گزارش میشود. از شکل چنین بر میآید که شتابهای طیفی (Sa) در دورههای تناوب بیشتر از ۰/۵ ثانیه، برای خاکهای نرم بزرگتر از خاکهای سختاند. این از آن روست که ضریبهای بزرگنمایی ![]() بسته به گونه خاک تغییر میکنند.
بسته به گونه خاک تغییر میکنند.
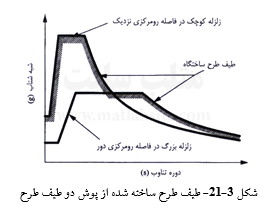
گاه در برخی ساختگاهها، طیف طرح، پو دو یا چند طیف طرح گوناگون است. چنین ساختگاههایی تحت تأثیر بیش از یک گسل فعال میباشند. طیفهای طرح به دست آمده از زمین لرزههای مربوط به چشمههای گسلی گوناگون، با یکدیگر متفاوتند. در شکل ۳-۲۱، طیفهای پاسخ طرح برای یک نمونه از این ساختگاهها نشان داده شده است. طیف نخست مربوط به یک گسل نزدیک میباشد که زمین لرزههای با بزرگای کوچک را پدید آورده است. طیف دوم از زمین لرزهای با بزرگای زیاد و از یک گسل دور به دست آمده است. بر این پایه، طیف طرح ساختگاه، همانند شکل ۳-۲۱، برابر پوش این دو طیف خواهد بود.
مثال ۳-۵
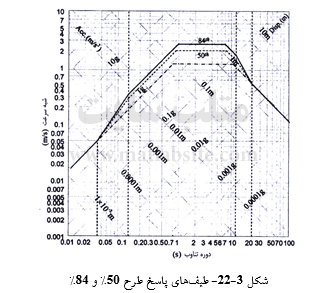
طیفهای پاسخ طرح ۵۰ و ۸۴ درصد را برای میرایی ۵% و با انگاشت خاک سخت، بر روی نمودار لگاریتمی چهار محوره رسم نمایید. فرض کنید که:
Ta=1.33s, Tb=1.8s, Te=1.10s, Tf=1.33s; ![]() =۰٫۶g.
=۰٫۶g.
پاسخ:
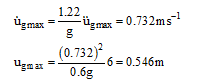
با انگاشت این مقادیر برای ![]() و نیز
و نیز ![]() برای میرایی ۵% و خاک سخت، طیف پاسخ طرح (طیف میانی) در یک نمودار چهار محوره (شکل ۳-۲۲) نشان داده شده است. در همین نمودار، طیف ۸۴% نیز نمایش داده شده است، که برای آن، نیز
برای میرایی ۵% و خاک سخت، طیف پاسخ طرح (طیف میانی) در یک نمودار چهار محوره (شکل ۳-۲۲) نشان داده شده است. در همین نمودار، طیف ۸۴% نیز نمایش داده شده است، که برای آن، نیز ![]() انگاشته شدهاند.
انگاشته شدهاند.
۵-۵-۳- زلزلههای پایه (مبنا)
طیفهای طرح با PSDF جنبش زمین، ورودیهای تحلیل سازهها هستند (که میبایست با توجه به تراز مناسب لرزش زمین برای انجام طراحی سازه، در دسترس طراحان قرار گیرند). تراز لرزش زمین با زلزله پایه (مبنا) مشخص میشود. عموماً زلزلههای پایه در پیوند با مفهوم طراحی دو ترازه بررسی میشوند: در یک تراز از لرزش زمین، امکان بهره برداری از سازه همچنان پابرجاست (آسیب در بازه پذیرفتنی است)، و در تراز دیگر، گسیختگی (یا آسیب) اساسی رخ میدهد، بی آن که سازه فرو ریزد . از آن جا که کمّی سازی و به اندازه در آوردن زلزله پایه نیازمند انگاشتن الزامات و ملاحظات فراوانی است، طیف پاسخ یا PSDF در نمایش بهنجار شده، در دسترس طراحان قرار میگیرد. بدین ترتیب، میتوان اهداف و الزامات مختلفی را در تحلیل منظور نمود .
تعاریف بسیار گوناگونی برای زلزله پایه در هر دو تراز پیشنهاد شده است:
(۱) زمین لرزههایی که تراز یا کران بالایی در چارچوب طراحی دو ترازه به شمار میروند (زلزله طرح):
زمین لرزه محتمل بیشینه (MCE) بزرگترین زلزلهای است که پیش بینی میشود از یک چشمه لرزهای پدید آید.
زلزله طراحی ایمن (SSE) در طراحی نیروگاههای هستهای کاربرد دارد و با بیشینه شتاب افقی زمین ارتباط دارد.
شناسههای دیگری که برای تعریف ترازهای مشابهی از زلزله به کار میروند، عبارتند از: زلزله محتمل طرح ، زلزله تراز ایمنی ، زلزله بیشینه طرح و …
(۲) زمین لرزه هایی که تراز یا کران پایینی در چارچوب طراحی دو ترازه به شمار میروند (زلزله بهره برداری):
کران پایین عمدتاً زلزله پایه بهره برداری (OBE) انگاشته میشود، که زمین لرزهای است که بیشترین احتمال رخداد را در طول عمر سازه دارد. دیگر شناسههای کاربردی برای این تراز، زمین لرزه عبارتند از: زلزله تراز بهره برداری ، زلزله محتمل بهره برداری ، و زلزله تراز مقاومت . OBE معمولاً نصف SSE انگاشته میشود.
۳-۵-۶- طیف پاسخ احتمالاتی
از آن چه تا کنون گذشت میتوان دریافت که طیف پاسخ طرح برای یک منطقه به عوامل بسیاری بستگی دارد که مهمترین آنها را میتوان گسلهای فعال اثر گذار بر منطقه، ساز و کار گسلی، بزرگای زمین لرزهها، ویژگیهای زمین شناختی منطقه، و شرایط خاک محلی دانست. پیش بینی زلزلههای آینده در منطقه حقیقتاً ناشدنی است، چرا که بسیاری از این عوامل نامعلوم هستند. بدین ترتیب، نمیتوان یک طیف پاسخ طرح قطعی را آن گونه که پیشتر معرفی شد، برای طراحی ایمن سازهها در برابر زلزلههای آینده، که اساساً ناشناخته هستند، کافی و بسنده دانست. از همین رو، پژوهشگران الگوهای احتمالاتی را برای نمایش طیفهای پاسخ آزمـودهانـد. این طیـفهای پاسخ در تحلیل و طراحی لرزهای احتمالاتی و یا تحلیل خطر پذیری احتمالاتی سازههای طراحی شده به کار میآیند. چنین طیفهایی از پردازش آماری دادههای ثبت شده زمین لرزههای منطقه ده دست میآیند و بیشتر به صورت رابطههایی تجربی در دسترس قرار میگیرند. شماری از رابطههای تجربی برای طیفهای پاسخ در بخش ۳-۷-۵ داده شده اند.
۳-۵-۷- طیفهای ویژه ساختگاه و طیفهای خطر یکنواخت
۳-۵-۷-۱ طیفهای ویژه ساختگاه
طیفهای ویژه ساختگاه متفاوت از طیفهای طرح هستند. طیفهای طرح با هدف کالی طراحی سازهها ساخته، و در آیین نامهها پیشنهاد میشوند. در مقابل، طیفهای ویژه ساختگاه، طیفهایی هستند که تنها و تنها برای طراحی سازهها در همان ساختگاه به کار میروند. سازههایی که با طیف ویژه ساختگاه طراحی میشوند، عموماً سازههایی ویژه هستند که میبایست شرایط ساختگاه در طراحی آنها به دقت لحاظ شوند.
همچنین، گاه به سبب شرایط خاص زمین شناسی، ژنوفیزیکی و ژئوتکنیکی ساختگاه، نگاشتهای زمین لرزههای گذشته در محل ساختگاه، مشخصاً متفاوت از دیگر نگاشتهای ثبت شده برای کل منطقه هستند. در چنین ساختگاههایی، طیفهای ویژه ساختگاه، با کمک یک دسته شتاب نگاشت برداشت شده در ساختگاه، به دست میآیند. در صورت نیاز، میتوان شتاب نگاشتهای برداشت شده در دیگر ساختگاههای دارای ویژگیهای مشابه زمینشناسی، لرزهشناسی و ژئوفیزیکی را نیز بدانها افزود. همه این شتاب نگاشتها برای بزرگای یکه و فاصله یک چشمه تا ساختگاه، مقیاس میشوند. عملیات مقیاس کردن در مورد ویژگیهای ساختگاه نیز انجام میگیرد. این مقیاس کردن به کمک تبدیل فوریه هر شتاب نگاشت انجام میپذیرد. با ضرب بخشهای حقیقی و موهومی نتایج تبدیل یافته در ضریبهای مقایس وابسته به بسامد، اثر تفاوتها در بزرگای زلزله و شرایط ساختگاه منظور میشوند. مقیاس کردن برای فاصله چشمه تا ساختگاه با ضرب نتایج در یک ضریب مقیاس مستقل از بسامد انجام می پذیرد. این ضریب مقیاس از رابطه کاهیدگی معتبر برای منطقه (رابطهای که PGA را به صورت تابعی از بزرگا و فاصله رومرکزی بیان میکند) به دست میآید. پس از اعمال این سه ضریب مقیاس، با استفاده از تبدیل وارون فوریه، مجموعه کامل شتاب نگاشتهای مقیاس شده سازگار با ساختگاه مورد نظر به دست خواهد آمد. طیفهای پاسخ به دست آمده از این شتاب نگاشتها، میانگین گیری و با شیوههای برازش نمودار، هموار سازی میشوند تا طیف ویژه ساختگاه مورد نظر در دسترس قرار گیرد.
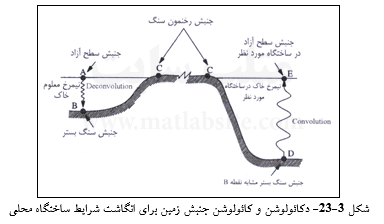
دستیابی به طیف دیگر ساختگاههای پیرامونی (مانند ساختگاه E در شکل ۳-۲۳) از روی نگاشتهای به دست آمده در یک ساختگاه (نقطه A در شکل ۳-۲۳)، نیازمند انجام دکائولوشن و تحلیل پاسخ زمین میباشد. دکالوشن، همان تحلیل پاسخ زمین به ترتیب وارون است که تاریخچه جنبش زمین را در بستر سنگی (نقطه B) به دست میدهد. این جنبش با جنبش بستر سنگی در نقطه D (شکل ۳-۲۳) یکسان است. بر این پایه، تاریخچه زمانی جنبش زمین در ساختگاه E که با شرایط دلخواه خاک محلی سازگار است، در دسترس قرار میگیرد.
مثال ۳-۶
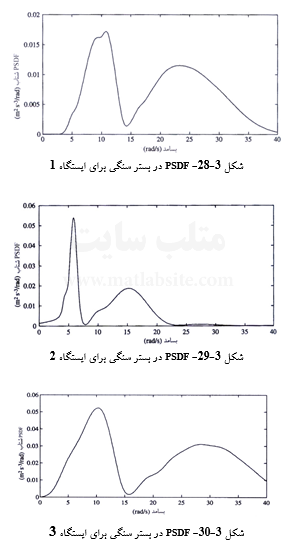
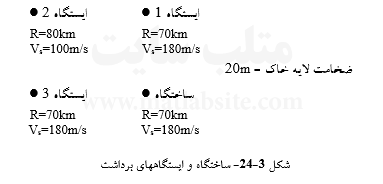
سه نگاشت شتاب زمین در پیرامون ساختگاه شکل ۳-۲۴، با PSDFهای نشان داده شده در شکلهای ۳-۲۵ تا ۳-۲۷، در دسترسند. شرایط خاک در ساختگاه محل برداشت نگاشتها، متفاوت از شرایط خاک در ساختگاهی است که طیف ویژه آن جستجو میگردد. فرض میشود که رابطه کاهیدگی پیشنهادی تورو (رابطه ۳-۴۶) (بخش ۳-۷-۱)، برای تراز سنگ بستر این منطقه معتبر است، و بخش عمده جنبش سطح زمین ناشی از امواج انتشار یافته زلزله در راستای قائم میباشد. طیف پاسخ ویژه ساختگاه را برای ۷=M با استفاده از این دادههای محدود بیابید. ς خاک را برابر ۰/۰۵ و مدت زمان زمین لرزه را ۲۵s ثانیه بپندارید.
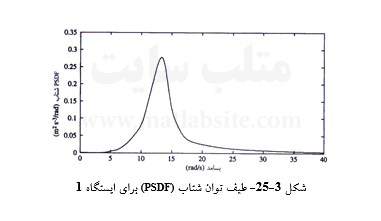
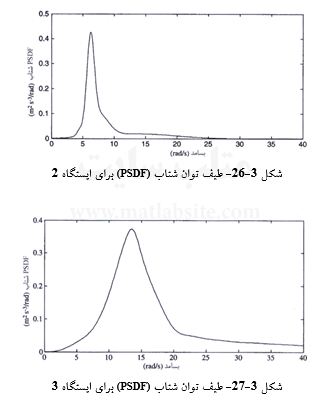
پاسخ:
در شکلهای ۳-۲۸ تا ۳-۳۰، طیفهای توان (PSDF)ها مربوط به نقاطی از سنگ بستر، درست در زیر ایستگاههای سطحی، نمایش داده شدهاند.
![]() (۳۵-۳- آ)
(۳۵-۳- آ)
![]()
(۳۵-۳- ب)
با توجه به اندر کنش خاک و سازه، رابطه زیر در دسترس خواهد بود:
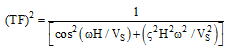 (۳۶-۳)
(۳۶-۳)
که H عمق لایه خاک روی سنگ بستر میباشد.
از محاسبه سطح زیر نمودارهای PSDF، انحراف معیارها برای شتابها چنین به دست میآیند:

P1، P2 و P3 ضریبهای بیشنه¬اند که از رابطه ۳-۱۹- آ- پ به دست میآیند.
با به کارگیری رابطه کاهیدگی پیشنهادی تورو، بزرگاهای نظیر PGAها در تراز سنگ بستر خواهد شد:
M1=6/2 M2=5/8 M3=7/3
PGA در سنگ بستر زیر ساختگاه برای ۷=M و R=100km برابر PGA=0/38g به دست میآید.
سه PSDF تراز سنگ بستر، با کمک رابطه زیر، به PGA برابر ۰/۳۸g مقیاس میشوند:
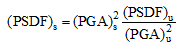
(۳۷-۳)
که
PSDF ،(PSDF)s مقیاس شده،
PSDF ،(PSDF)u اولیه یا مقیاس نشده،
PGA ،(PGA)u برای PSDF مقیاس نشده، و
PGA ،(PGA)s برای PSDF مقیاس شده
میباشند.
در محاسبات بالا، فرض بر آن است که ضریبهای بیشینه برای PSDF های مقیاس شده و مقیاس نشده یکسان هستند. سه PSDF مقیاس شده در شکلهای ۳-۳۱ تا ۳-۳۳ نشان داده شدهاند. PSDFهای همتا در سطح زمین (در محل ساختگاه) با رابطه ۲-۳۵-آ به دست میآیند:
![]() (۳۸-۳)
(۳۸-۳)
سه PSDF ای که بدین گونه برای ساختگاه به دست آمدهاند، در شکل ۳-۳۴ تا ۳-۳۶ نشان داده شدهاند. روند بالا، همسنگ با همان فرآیند مقیاس کردن مؤلفههای فوریه سه نگاشت زمانی جنبش زمین در پیرامون ساختگاه به منظور سازگاری با شرایط خاک، بزرگای زلزله (برابر ۷)، و فاصله چشمه تا سطح میباشد.
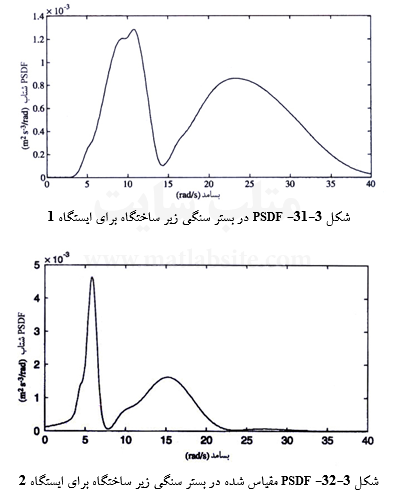
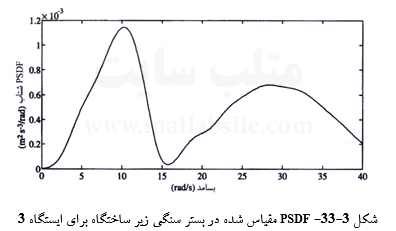
از این سه PSDF، سه نگاشت تاریخچه زمانی جنبش زمین به صورت مصنوعی و بر پایه راهکار بخش ۳-۶-۲ ساخته میشوند، و طیفهای پاسخ آنها به دست میآیند (بخش ۳-۵-۱). این طیفها در شکلهای ۳-۳۷ تا ۳-۳۹ نشان داده شده¬اند. میانگین این سه، طیف پاسخ ویژه ساختگاه است که نمایش آن در شکل ۳-۴۰ آمده است.
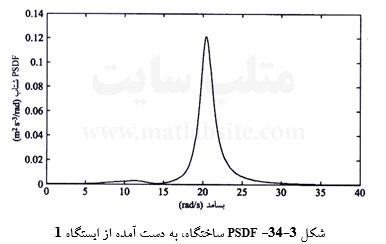
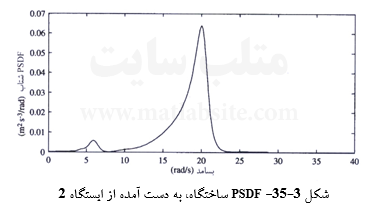
ادامه دارد ….
آنچه مطالعه کردید، بخش هایی از «فصل دوم» کتاب «بهینه کنترل فعال سازه با رویکرد کلاسیک و هوش مصنوعی» تالیف «جواد پالیزوان (مدرس دانشگاه) و زند علی روشنی (مدرس دانشگاه)»، می باشد که در راستای معرفی و انتشار رایگان جهت استفاده مخاطبین متلب سایت در اختیار این مجموعه قرار داده شده است.
برای تهیه این کتاب می توانید به این لینک(+) مراجعه نمایید.
همچنین آموزش های زیر در فرادرس نیز مباحثی مرتبط با محتوای این کتاب را پوشش می دهند:
مجموعه: معرفی کتاب, مهندسی عمران برچسب ها: Optimal active structural Control, پیش بینی شناسه های ورودی لرزهای, تابع چگالی طیفی, جنبش زمین, زلزله های پایه, شتاب نگاشت های مصنوعی, شناسه های ورودی لرزهای, طیف انرژی, طیف پاسخ زمینلرزه, طیف پاسخ طرح, طیف ترکیبی D-V-A, طیف فوریه, طیف های جابجایی, طیف های خطر یکنواخت, طیف های ساختگاه, طیف های سرعت و شتاب, طیف های ویژه ساختگاه, نگاشت های مصنوعی




 (No Ratings Yet)
(No Ratings Yet)