آموزش کنترل خطی – مرور مفاهیم
تعریف سیستم:
یک سیستم به مفهوم کلی، ترکیبی از اجزایی است که کارکرد آنها با یکدیگر، مقصود مشخصی به انجام می رسد و در یک تعریف رسمی، عبارت است از مجموعه ای از اجزا، که با انجام عملیات بر روی یک یا تعدادی سیگنال مقصودی خاصی را به انجام می رساند و در نتیجه سیگنال یا سیگنال های جدیدی را تولید می کند.

فهرست:
- تعریف های پایه در سیستم های کنترل
- نمایش سیستم های کنترل خطی
- تحلیل عملکرد گذرا و ماندگار سیستم های کنترل
- تحلیل پایداری در سیستم های کنترل
- مکان هندسی ریشه ها
- نمودارهای بودی
- نمودارهای نایکویست
- جبران سازها
تعریف سیستم:
یک سیستم به مفهوم کلی ترکیبی از اجزایی است که با کارکرد آنها با یکدیگر، مقصود مشخصی به انجام میرسد و در یک تعریف رسمی عبارتست از مجموعهای از اجزا که با انجام عملیات بر روی یک یا تعدادی سیگنال مقصودی خاصی را به انجام میرساند و در نتیجه سیگنال یا سیگنالهای جدیدی را تولید میکند
هدف سیستم کنترل: کنترل خروجی ها به کمک اعمال ورودی ها توسط اجزای سیستم کنترل به روشی مشخص. به قولی یافتن ورودی که بتواند خروجی مطلوب را ایجاد کند.
توصیف سیستم:
- نمایش تابع تبدیل
- نمایش فضای حالت
- نمایش معادلات دیفرانسیل
نمایش معادلات دیفرانسیل:
معادله دیفرانسیل هر سیستم خطی به صورت زیر می باشد:
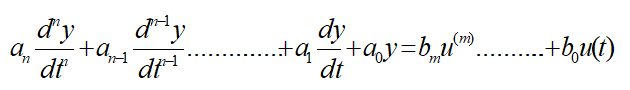
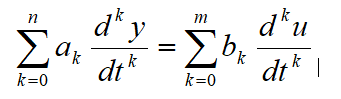
میتوان از طرفین لاپلاس بگیریم:
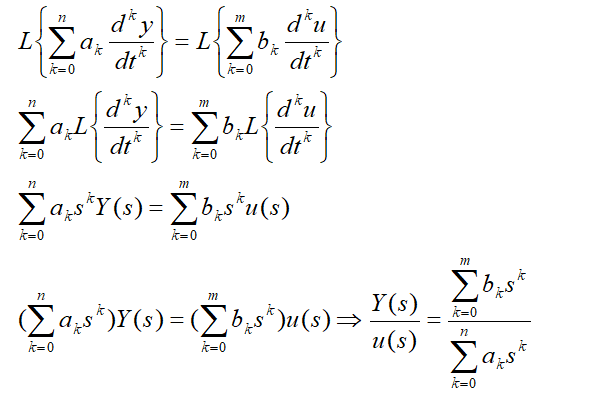
انتگرال کانولوشن:
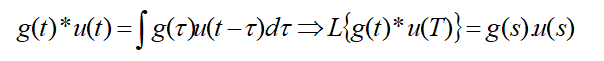
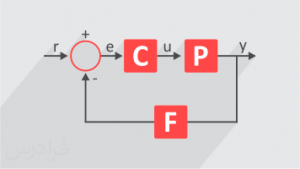
بلوک دیاگرام:
به منظور مدل سازی یک سیستم با استفاده از بلوک دیاگرام، لازم است در ابتدا با اجزاء بلوک دیاگرام آشـنا شد.
جبر بلوک دیاگرامها: قواعد حاکم بر ساده سازی بلوک دیاگرام
- جمع
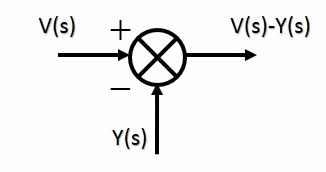
- سری کردن

- موازی کردن
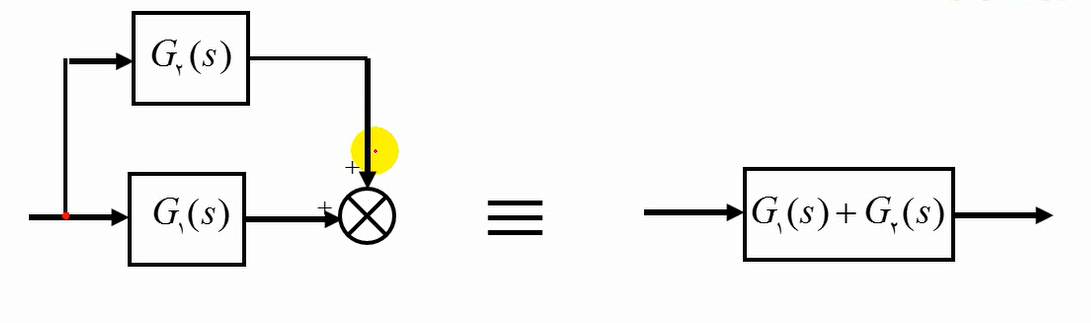
- فیدبک
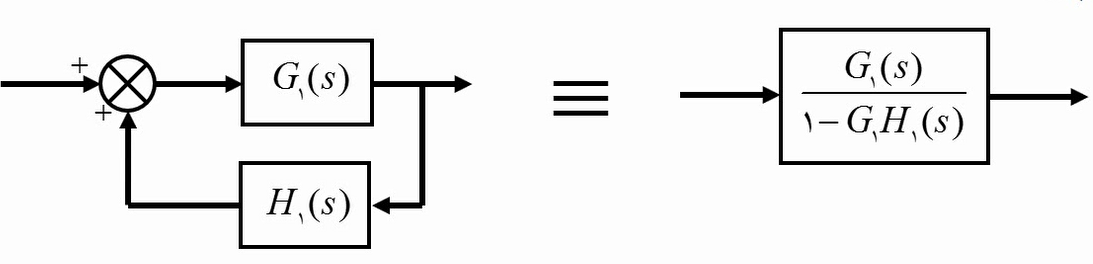
نمودار گذر سیگنال (Signal Flow Graph):
گره ورودی: گره ای که هیچ شاخه وارد شونده ای نداشته باشد.
گره خروجی: گره ای که هیچ شاخه خارج شـونده ای نداشـته باشـد.
مسیر: مجموعه ای از شاخه های هم جهت از گره مبدأ به گره مقصد به گونه ای کـه طی مسیر از هر گره حداکثر یکبار عبور شود.
مسیر پیشرو: هر مسیری از گره ورودی به گره خروجی.
حلقه: مجموعه ای از شاخه های هم جهت از که از یک گره مبدأ شروع شده و نهایتاً به همـان گره ختم شده باشد، به گونه ای که طی مسیر از هر گره حداکثر یکبار عبور شود. به عبارت دیگـر مـی تـوان گفت حلقه، مسیری است که در آن گره مبدأ و مقصد بر هم منطبق باشند.
بهره مسیر: حاصلضرب بهره های شاخه های تشکیل دهنده هـر مـسیر را بهره مسیر گویند.
بهره حلقه: حاصلضرب بهره های شاخه های تشکیل دهنده هـر حلقـه را بهره حلقه گویند.
حلقه های غیر مماس: حلقه های مماس حلقه هایی هستند که حداقل در یک گره مشترک باشند، ولی حلقه های غیر مماس در هیچ گره ای مشترک نیستند.
قاعده میسون:
یکی از روشهای ساده برای به دست آوردن تابع تبدیل کل یک سیستم:
P= 1/ ∆ * ∑ Pk* ∆k
Pk : امین مسیر پیشرو k بهره انتقال
∆-۱=∑La + ∑Lb Lc -∑ Ld Le Lf
فضای معادلات
متغیر حالت متغیری است که مشتقش وابسته به سایر متغیرهای سیستم است:
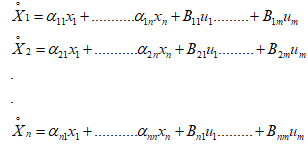
میتوان معادلات بالا را به فرم ماتریسی نوشت:
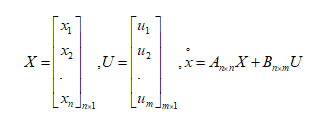
به طور کلی در تحلیل رفتار دینامیکی سیستم ها، در حوزه زمان، دو دسته از مشخصات کنترلی مورد مطالعه قرار می گیرد:
- پاسخ ماندگار
- پاسخ گذرا
پاسخ ماندگار:
این مشخصات، بیانگر آن است که پاسخ سیستم مورد مطالعه در صورت پایدار بودن، آیا توانایی دنبال کردن ورودی مرجع را دارد و یا اینکه در حالت دائمی، بین پاسخ سیستم و ورودی فرمان، خطـای مانـدگار و جـود خواهد داشت. به ایت ترتیب ملاحظه می شود که شرط بررسی مشخصات ماندگار، پایداری سیستم است که اصلی ترین هدف کنترل به شمار می رود به گونه ای که هر خواسته مطلوب کنترلی، پس از حصول اطمینان از پایداری، قابل بحث خواهد بود.
پاسخ گذرا:
این دسته از مشخصات به شکل تغییرات پاسخ سیستم در طول زمان (از لحظه شروع) و نحوه میل آن به مقدار دائمی ارتباط دارند.
پاسخ ورودی های خاص در سیستم مرتبه اول
پاسخ سیستم مرتبه ۱ به ورودی ضربه
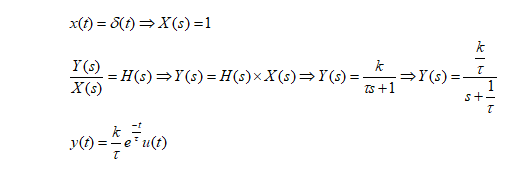
پاسخ سیستم مرتبه ۱ به ورودی پله
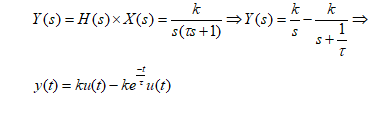
سیستم های مرتبه ۲
تابع تبدیل در سیستم های مرتبه دو به صورت:
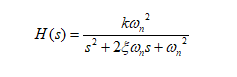
محاسبه پاسخ سیستم مرتبه ۲ به ورودی ضربه:
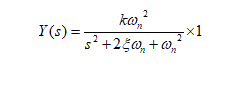
محاسبه پاسخ سیستم مرتبه ۲ به ورودی پله:
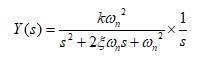
الف: حالت نامیرا ![]()
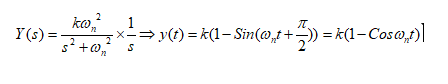
ب: حالت زیر میرایی ![]()

مقدار نهایی پاسخ پل k
فرکانس ظاهری نوسان
![]()
زمان نشست
![]()
زمان پیک
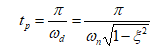
Overshoot
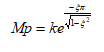
ج. ![]() حالت میرایی بحرانی
حالت میرایی بحرانی
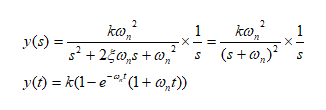
د. ![]() حالت فوق میرا
حالت فوق میرا
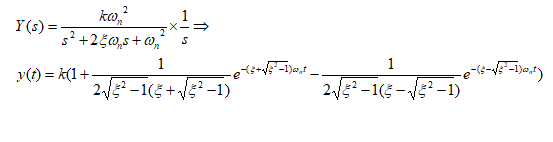
معیار پایداری روث – هرویتز:
G(s)=N(s)/D(s)
شرط پایداری این سیستم آن است که تمامی قطب های تابع تبدیل در سمت چپ محور موهومی قرار گرفته باشند.
مشکل اصلی در راستای تحلیل پایداری سیستم بر اساس این تعریف، عدم وجود یک روش تحلیلی جامع برای محاسبه تمامی ریشه های چندجمله ای مشخصه سیستم است. بنابراین به عنوان یک راه حل برای تحلیل پایداری سیستم بدون نیاز به محاسبه ریشه های چندجمله ای مشخصه، استفاده از معیار روث – هرویتز است که دارای دو شرط لازم و کافی می باشد.
شرط لازم: تمامی ضرایب چند جمله ای مشخصه مخالف صفر و هم علامت باشند.
شرط کافی: برای بررسی شرط کافی ابتدا جدول (آرایه) روث را مطابق روش زیر تشکیل می دهیم.

پس از تکمیل جدول روث برای بررسی شرط کافی عناصر ستون اول را در نظر می گیریم. اگر تمامی عناصر ستون اول غیر صفر و هم علامت (هیچ تغییر علامتی در ستون اول نباشد) باشند، به این معنی است که تمام ریشه های چند جمله ای مشخصه در سمت چپ محور موهومی قرار دارند. در غیر این صورت به تعداد تغییر علامت های صورت گرفته در عناصر ستون اول، ریشه سمت راست وجود دارد.
حالتهای خاص
الف. در تشکیل جدول روث اگر اولین عنصر از یک سطر صفر گردد، در این حالت صفر را با اپسیلون جایگذاری کرده و اپسیلون را به سمت صفر میل می دهیم.
ب. اگر در تشکیل جدول روث یک ردیف تمام صفر اتفاق بیفتد، به معنای وجود ریشه های قرینه است. در این صورت برای تعیین وضعیت ریشه های قرینه با استفاده از عناصر ردیف قبل از ردیف تمام صفر یک چند جمله ای کمکی می نویسیم. ضرایب مشتق چند جمله ای کمکی را جایگزین عناصر ردیف تمام صفر می کنیم و براساس آن جدول روث را تکمیل می کنیم.
مکان هندسی ریشه ها:
مراحل رسم مکان هندسی ریشه ها به صورت زیر است:
الف. به اندازه درجه معادله مشخصه مکان هندسی شاخه دارد.
ب. هر نقطه ای از محور حقیقی که تعداد کل صفرها و قطب های حلقه باز سمت راست آن فرد باشد، جزء مکان هندسی قطب های حلقه بسته خواهد بود.
ج. مکان هندسی قطب های حلقه بسته از قطب های حلقه باز شروع شده و به صفرهای حلقه باز ختم می گردد.
د. تعیین مجانب ها: برای رسم شاخه هایی از مکان هندسی که به ازای صفرهای بی نهایت حلقه باز به بی نهایت ختم شده و یا به ازای قطب های در بی نهایت حلقه باز از بی نهایت آعاز می شوند، لازم است که مجانب های مربوطه را به دست آوریم. برای این منظور خواهیم داشت:
محل تقاطع مجانب ها روی محور حقیقی:
δ = ∑pi – ∑zi/n-m
زوایای مجانب ها:
Θ =(۲M+1)* π/n-m
ی. محاسبه نقاط شکست:
- ریشه های dk/ds را محاسبه می کنیم.
- ریشه هایی که K متناظر با آنها از رابطه K=-1/G(s) صدق کنند، نقطه شکست است.
ز. محاسبه نقاط قطع مکان هندسی با محور موهومی:
استفاده از روش روث – هرویتز
زاویه خروج از قطب:
Θz1-( Θp1+ Θp2 + Θp4 + Θd1)=-(1+2k)*180
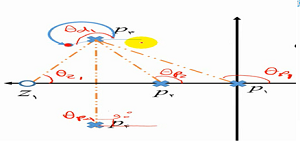
زاویه ورود به صفر:
(Θd2+ 90 (-180 + 2*135 +135)= -180

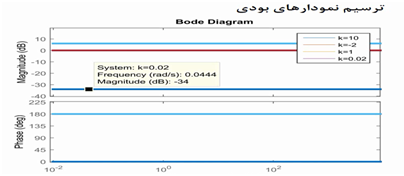
نمودارهای بودی
در این نمودارها اندازه و فاز تابع تبدیل در دو نمودار رسم می شود.
روش رسم نمودار بودی:
تابع تبدیل را به صورت جمع عوامل پایه می نویسیم و جدا با هم جمع می کنیم.
عوامل پایه در نمودار بودی:
الف. گین k
ب. مشتق گیر ![]() انتگرال گیر
انتگرال گیر ![]()
ج. قطب حقیقی ![]()

د. صفر حقیقی
تنها تفاوتش با قطب حقیقی در این است که در T شیب ۲۰ دسی بل زیاد می شود.
و. صفر مختلط و قطب مختلط
۱+(۲zeta/Wn)*s+(1/Wn2 )*S2 OR [ 1+(2zeta/Wn)*s+(1/Wn2 )*S2 ]-1
صفر مختلط در فرکانس (Wn) 40 دسی بل شیب را زیاد می کند.
قطب مختلط در فرکانس (Wn) 40 دسی بل شیب را کم می کند.
نمودارهای قطبی (دیاگرام نایکوییست)
در رسم نمودارهای قطبی (دیاگرام نایکوییست) چند نقطه مهم هستند:
W=0
W=inf
برخورد با محور حقیقی و محور موهومی
کافیست اندازه و فاز نقاط بالا را بدست آورده و به هم وصل کنیم.
حالت های خاص دیاگرام نایکوییست:
- قطب حقیقی
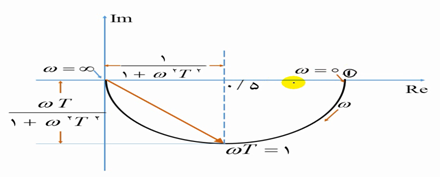
- صفر حقیقی

- قطب مختلط مزدوج (عامل مرتبه دو)
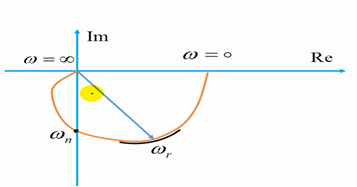
معیاری پایداری نایکوئیست: Z=n+p
Z = تعداد قطبهای حلقه بسته سمت راست
N =تعداد دورهای -۱
P = تعداد قطبهای حلقه باز سمت راست
حاشیه بهره: با تغییر بهره سیستم مکان ریشه های حلقه بسته تغییر می کند بنابر این سیستم ممکن است ناپایدار شود. مقدار بهره ای که به ازای آن اندازه ۱ و فاز ۱۸۰ شود، سیستم را در مرز ناپایداری قرار می دهد.
|G(jw1)|=1/a
حاشیه فاز
PM=-180 +angle(G(jw2))
انواع جبران سازها:
- پیش فاز
- پس فاز
- پیش فاز _ پس فاز
تابع تبدیل جبران ساز پیش فاز به فرم زیر است:
Gc(s)=a * 1+Ts/1+aTs
Wm=1/a1/2 *T
Sin( qm)=1-a/1+a
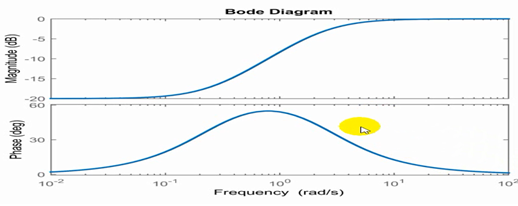
تابع تبدیل جبران ساز پس فاز به فرم زیر است:
G(s)=1+Ts/1+BTs
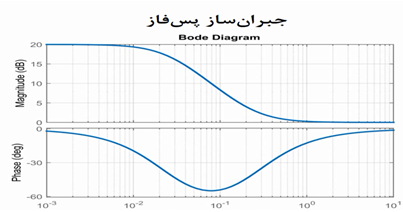
تابع تبدیل جبران ساز پیش فاز _ پس فاز به فرم زیر است:
G(s)=KcBa * (1+T1s)(1+T2S)/(1+aT1S)(1+BT2S)
مجموعه: اخبار و تازه ها




 (No Ratings Yet)
(No Ratings Yet)