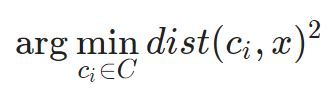الگوریتم‌های «خوشه بندی» (Clustering) از جمله روش‌های «یادگیری نظارت نشده» (Unsupervised LEarning) هستند. از این الگوریتم‌ها هنگامی استفاده می‌شود که داده‌های برچسب‌دار موجود نباشند. الگوریتم K-Means یکی از روش‌های محبوب و پرکاربرد خوشه‌بندی است. هدف این الگوریتم پیدا کردن گروه‌ها (خوشه‌ها) در مجموعه داده‌ای است که به عنوان ورودی دریافت می‌کند. در این مطلب، پیاده‌سازی الگوریتم K-Means با استفاده از «زبان برنامه‌نویسی پایتون» (Python Programming Language) انجام می‌شود.

خوشه‌بندی K-Means 

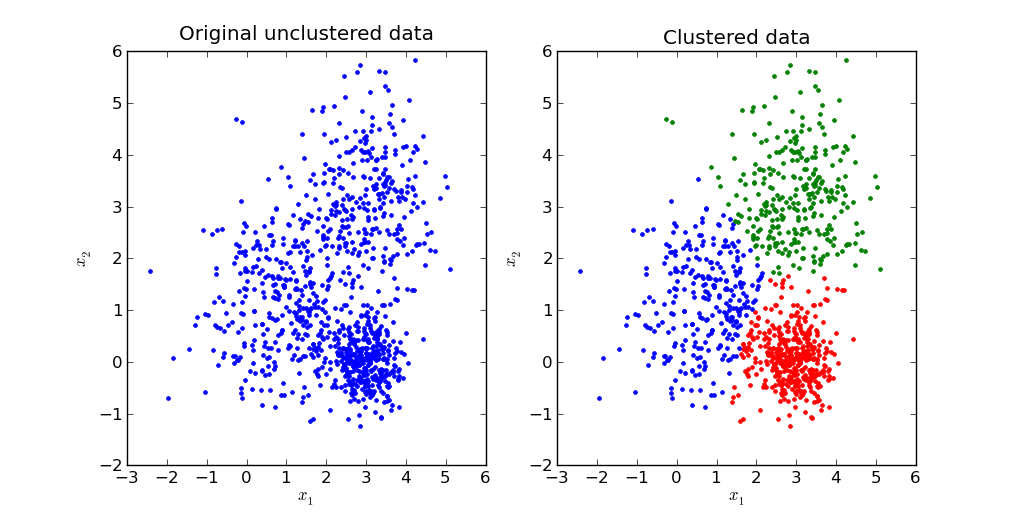
K-Means یک الگوریتم بسیار ساده است که داده‌ها را در K خوشه، گروه‌بندی می‌کند. تصویر زیر، مثالی از خوشه‌بندی K-Means است.

کاربردها

K-Means به طور گسترده‌ای در کاربردهای گوناگون مورد استفاده قرار می‌گیرد. از جمله این کاربردها می‌توان به موارد زیر اشاره کرد.

• بخش‌بندی تصاویر
• خوشه‌بندی داده‌های بخش‌بندی ژن
• خوشه‌بندی مقالات خبری
• خوشه‌بندی گونه‌ها
• تشخیص ناهنجاری

الگوریتم

الگوریتم K-Means، با فرض داشتن ورودی‌های x_n ،… ،x₃ ،x₂ ،x₁ به شکل زیر کار می‌کند. 

• گام اول: انتخاب K‌ نقطه تصادفی به عنوان مرکز خوشه‌ها که به آن «مرکزوار» (Centroid) گفته می‌شود.
• گام دوم: هر x_i به نزدیک‌ترین خوشه با محاسبه فاصله آن از هر مرکزوار تخصیص داده می‌شود.
• گام سوم: پیدا کردن مرکز خوشه‌های جدید با محاسبه میانگین نقاط تخصیص داده شده به یک خوشه
• گام ۴: تکرار گام ۲ و ۳ تا هنگامی که هیچ یک از نقاط تخصیص داده شده به خوشه‌ها تغییر نکنند.

انیمیشن بالا، مثالی از اجرای الگورتیم K-Means روی داده‌های دوبُعدی است. 

گام اول

K مرکز خوشه (مرکزوار) به طور تصادفی انتخاب می‌شوند. فرض می‌شود که این مرکزوارها c_k ،… ،c₃ ،c₂ ،c₁ هستند. می‌توان گفت که:

C = c₁, c₂, …, c_k

C مجموعه‌ای از همه مرکزوارها است.

گام دوم

در این گام، هر مقدار ورودی به نزدیک‌ترین مرکز تخصیص داده می‌شود. این کار با محاسبه فاصله اقلیدسی (L2) بین نقطه و هر مرکزوار انجام می‌شود.

که در آن (.)dist فاصله اقلیدسی است.

گام سوم

در این گام، مرکزوار جدید با محاسبه میانگین کلیه نقاط اختصاص داده شده به هر خوشه محاسبه می‌شود.

S_i مجموعه‌ای از همه نقاط تخصیص داده شده به خوشه i^th است.

گام چهارم

در این گام، مراحل ۲ و ۳ تکرار می‌شوند تا هیچ یک از نقاط تخصیص داده شده به خوشه‌ها تغییر نکنند. این یعنی تا هنگامی که خوشه‌ها پایدار شوند، الگوریتم تکرار می‌شود.

انتخاب مقدار K 

معمولا مقدار K مشخص است. در صورتی که مقدار K مشخص باشد، از آن برای خوشه‌بندی استفاده می‌شود. در غیر این صورت، روش Elbow برای تعیین K مورد استفاده قرار می‌گیرد.

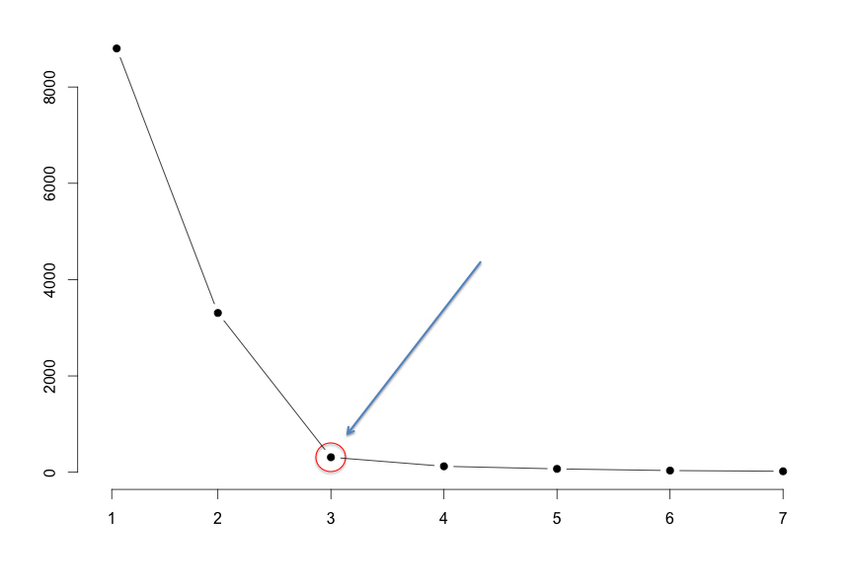الگوریتم برای مقادیر متفاوت K (مثلا از k = ۱ الی ۱۰) اجرا می‌شود و نمودار «مجموع مربعات خطا» (Sum of Squared Errors | SSE) بر حسب مقدار K ترسیم می‌شود. سپس، مقدار K برای نقطه elbow چنانکه در تصویر نمایش داده شده، انتخاب می‌شود.

پیاده‌سازی با استفاده از پایتون

مجموعه داده‌ای که مورد استفاده قرار می‌گیرد دارای ۳۰۰۰ ورودی و ۳ خوشه است. بنابراین، در حال حاضر مقدار K مشخص است. برای دسترسی به مجموعه داده کامل، می‌توان به گیت‌هاب [+] مراجعه کرد. کار با ایمپورت کردن مجموعه داده آغاز می‌شود.

%matplotlib inline
from copy import deepcopy
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
plt.rcParams[‘figure.figsize’] = (16, 9)
plt.style.use(‘ggplot’)

 

# Importing the dataset
data = pd.read_csv(‘xclara.csv’)
print(data.shape)
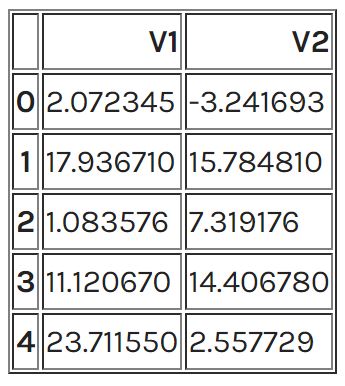
data.head()

خروجی:

(۳۰۰۰, ۲)

# Getting the values and plotting it
f1 = data[‘V1’].values
f2 = data[‘V2’].values
X = np.array(list(zip(f1, f2)))
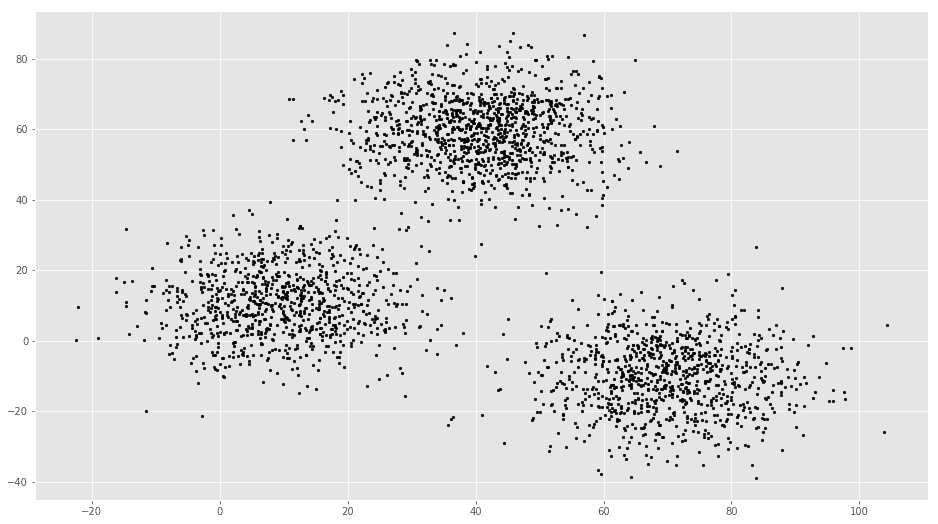
plt.scatter(f1, f2, c=’black’, s=7)

# Euclidean Distance Caculator
def dist(a, b, ax=1):
return np.linalg.norm(a – b, axis=ax)

# Number of clusters
k = 3
# X coordinates of random centroids
C_x = np.random.randint(0, np.max(X)-20, size=k)
# Y coordinates of random centroids
C_y = np.random.randint(0, np.max(X)-20, size=k)
C = np.array(list(zip(C_x, C_y)), dtype=np.float32)
print(C)

خروجی:

[[ ۱۱٫ ۲۶٫]
[ ۷۹٫ ۵۶٫]
[ ۷۹٫ ۲۱٫]]

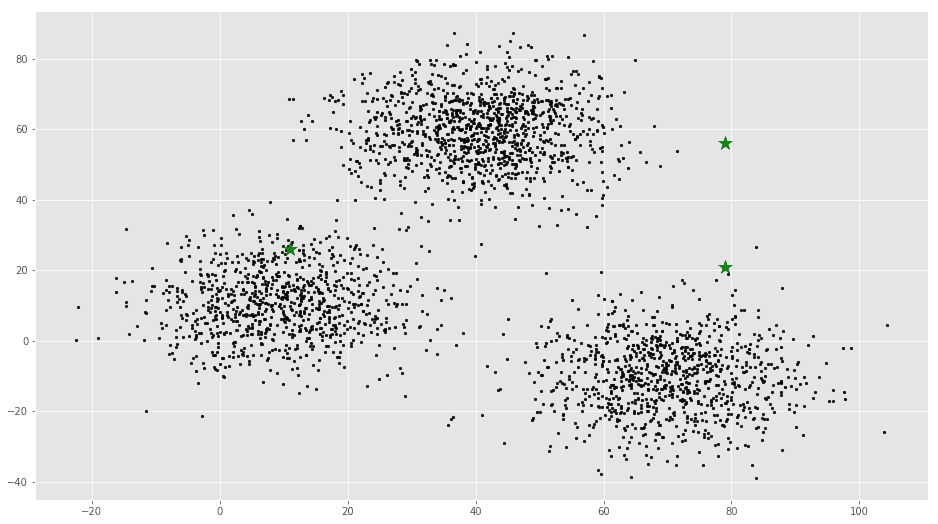
# Plotting along with the Centroids
plt.scatter(f1, f2, c=’#050505′, s=7)
plt.scatter(C_x, C_y, marker=’*’, s=200, c=’g’)

# To store the value of centroids when it updates
C_old = np.zeros(C.shape)
# Cluster Lables(0, 1, 2)
clusters = np.zeros(len(X))
# Error func. – Distance between new centroids and old centroids
error = dist(C, C_old, None)
# Loop will run till the error becomes zero
while error != 0:
# Assigning each value to its closest cluster
for i in range(len(X)):
distances = dist(X[i], C)
cluster = np.argmin(distances)
clusters[i] = cluster
# Storing the old centroid values
C_old = deepcopy(C)
# Finding the new centroids by taking the average value
for i in range(k):
points = [X[j] for j in range(len(X)) if clusters[j] == i]
C[i] = np.mean(points, axis=0)
error = dist(C, C_old, None)

 

colors = [‘r’, ‘g’, ‘b’, ‘y’, ‘c’, ‘m’]
fig, ax = plt.subplots()
for i in range(k):
points = np.array([X[j] for j in range(len(X)) if clusters[j] == i])
ax.scatter(points[:, 0], points[:, 1], s=7, c=colors[i])
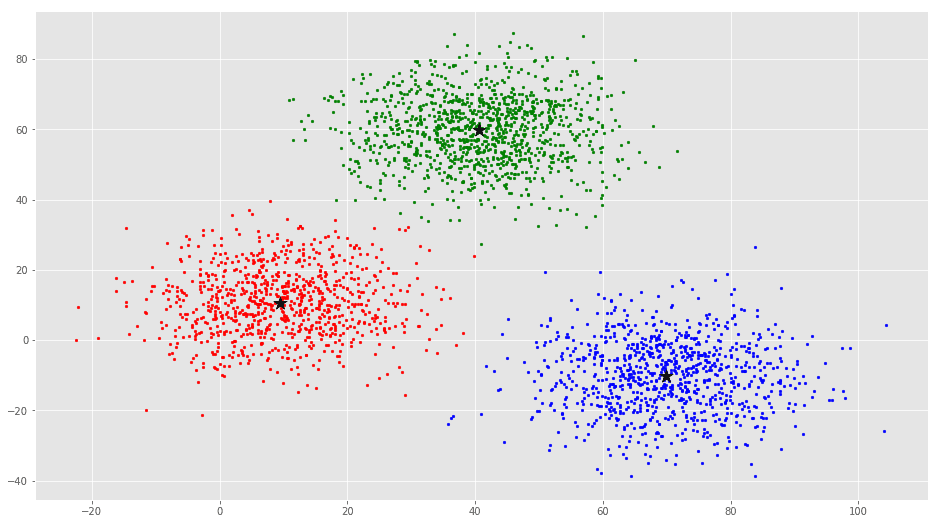
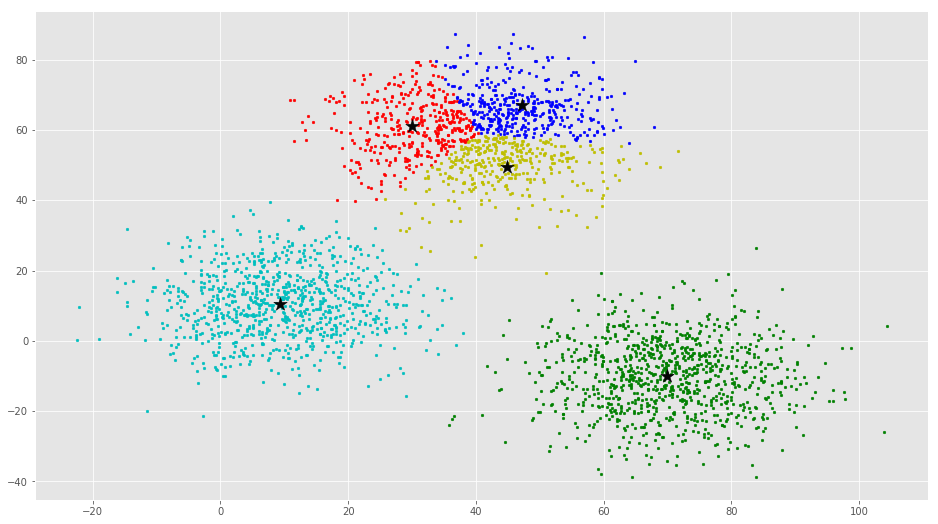
ax.scatter(C[:, 0], C[:, 1], marker=’*’, s=200, c=’#050505′)

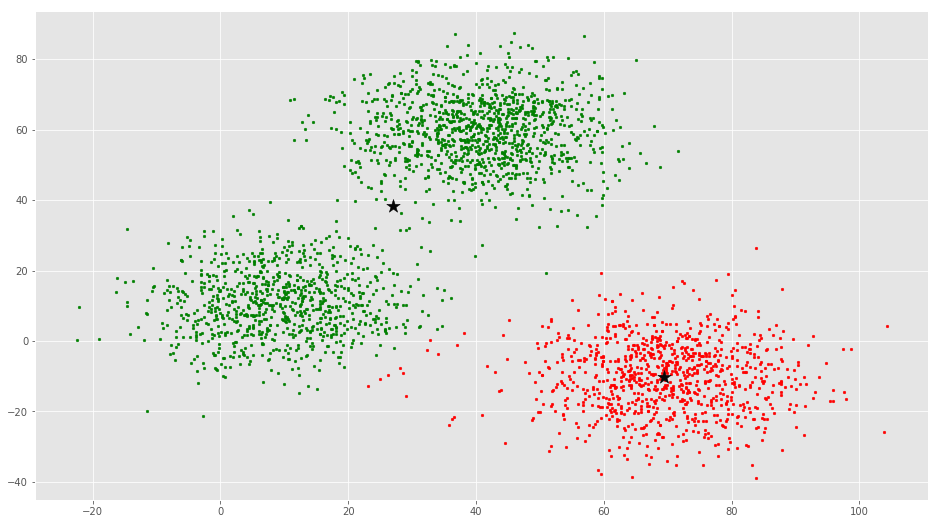
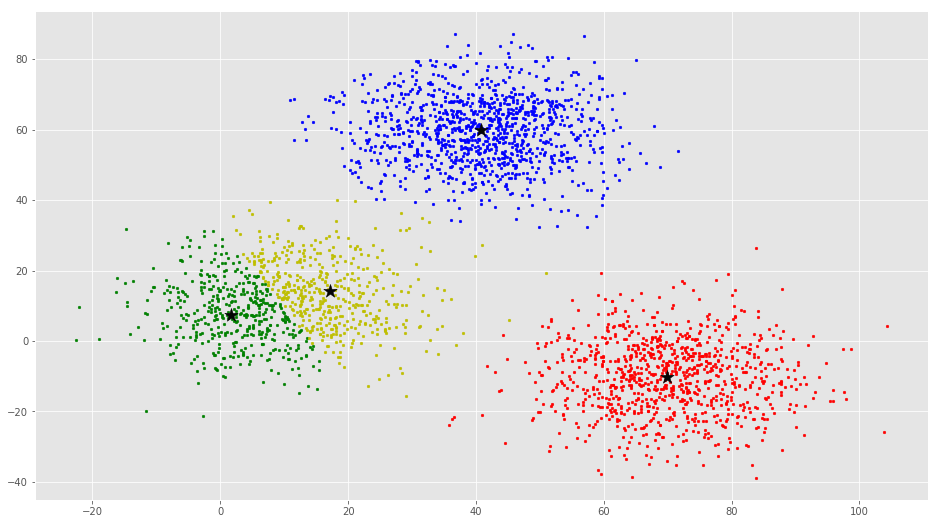
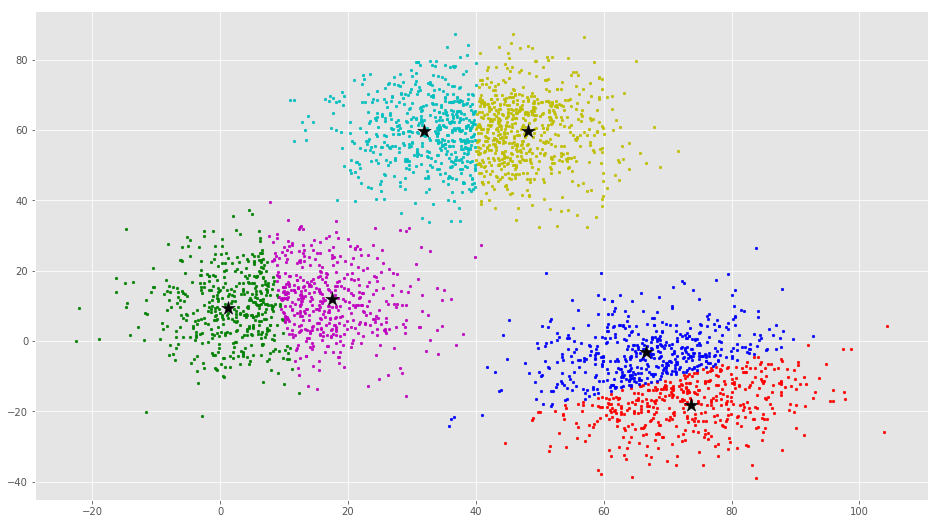
از این بصری‌سازی واضح است که سه خوشه وجود دارد که مراکز دسته آن‌ها با ستاره‌های مشکی مشخص شده است. اگر الگوریتم K-Means با مقدار اشتباهی از K اجرا شود، خوشه‌های کاملا اشتباهی حاصل می‌شود. اگر K-Means با مقادیر ۲، ۴، ۵ و ۶ اجرا شود، خوشه‌های زیر حاصل می‌شود.

در ادامه، چگونگی پیاده‌سازی خوشه‌بندی K-Means با استفاده از کتابخانه Scikit-Learn پایتون، بیان شده است.

پیاده‌سازی K-Means با کتابخانه Scikit-Learn

در مثال بیان شده در این قسمت، از همان مجموعه داده بالا استفاده می‌شود.

from sklearn.cluster import KMeans

# Number of clusters
kmeans = KMeans(n_clusters=3)
# Fitting the input data
kmeans = kmeans.fit(X)
# Getting the cluster labels
labels = kmeans.predict(X)
# Centroid values
centroids = kmeans.cluster_centers_

 

# Comparing with scikit-learn centroids
print(C) # From Scratch
print(centroids) # From sci-kit learn

خروجی:

[[ ۹٫۴۷۸۰۴۵۴۶ ۱۰٫۶۸۶۰۵۲۳۲]
[ ۴۰٫۶۸۳۶۲۸۰۸ ۵۹٫۷۱۵۸۹۲۷۹]
[ ۶۹٫۹۲۴۱۸۶۷۱ -۱۰٫۱۱۹۶۴۱۳ ]]
[[ ۹٫۴۷۸۰۴۵۹ ۱۰٫۶۸۶۰۵۲ ]
[ ۶۹٫۹۲۴۱۸۴۴۷ -۱۰٫۱۱۹۶۴۱۱۹]
[ ۴۰٫۶۸۳۶۲۷۸۴ ۵۹٫۷۱۵۸۹۲۷۴]]

می‌توان مشاهده کرد که مقادیر مرکزوارها مساوی اما ترتیب آن‌ها متفاوت است. مثال دیگری در ادامه ارائه می‌شود. برای این مثال، یک مجموعه داده با استفاده از تابع make_blobs ساخته می‌شود.

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

plt.rcParams[‘figure.figsize’] = (16, 9)

# Creating a sample dataset with 4 clusters
X, y = make_blobs(n_samples=800, n_features=3, centers=4)

 

fig = plt.figure()
ax = Axes3D(fig)
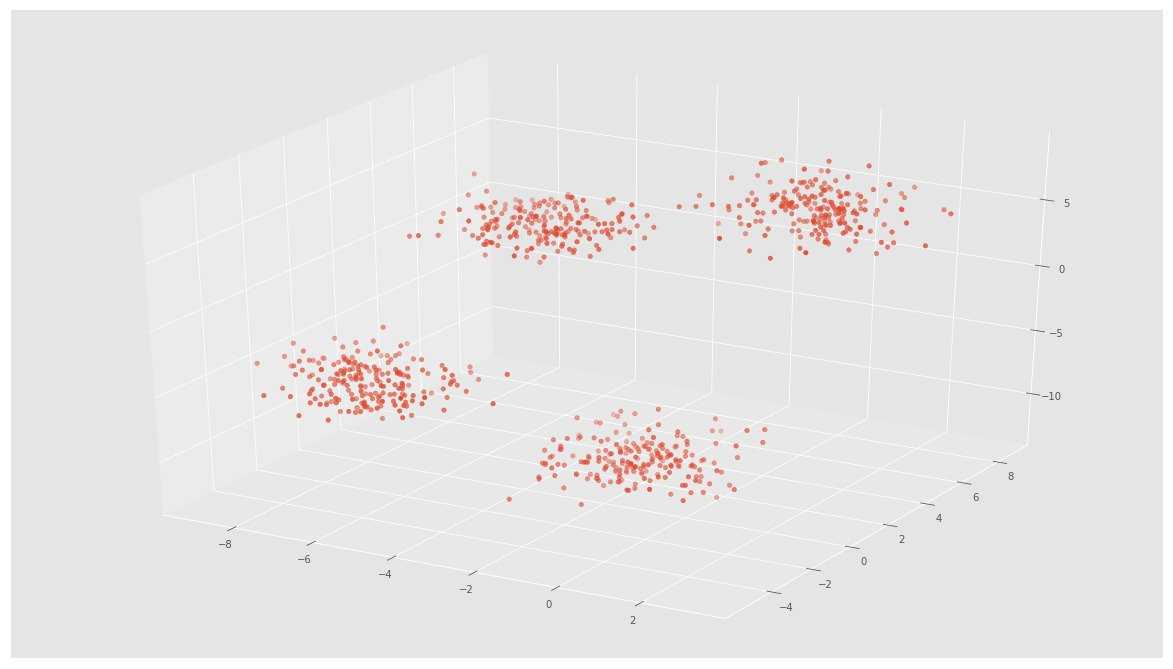
ax.scatter(X[:, 0], X[:, 1], X[:, 2])

# Initializing KMeans
kmeans = KMeans(n_clusters=4)
# Fitting with inputs
kmeans = kmeans.fit(X)
# Predicting the clusters
labels = kmeans.predict(X)
# Getting the cluster centers
C = kmeans.cluster_centers_

 

fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y)
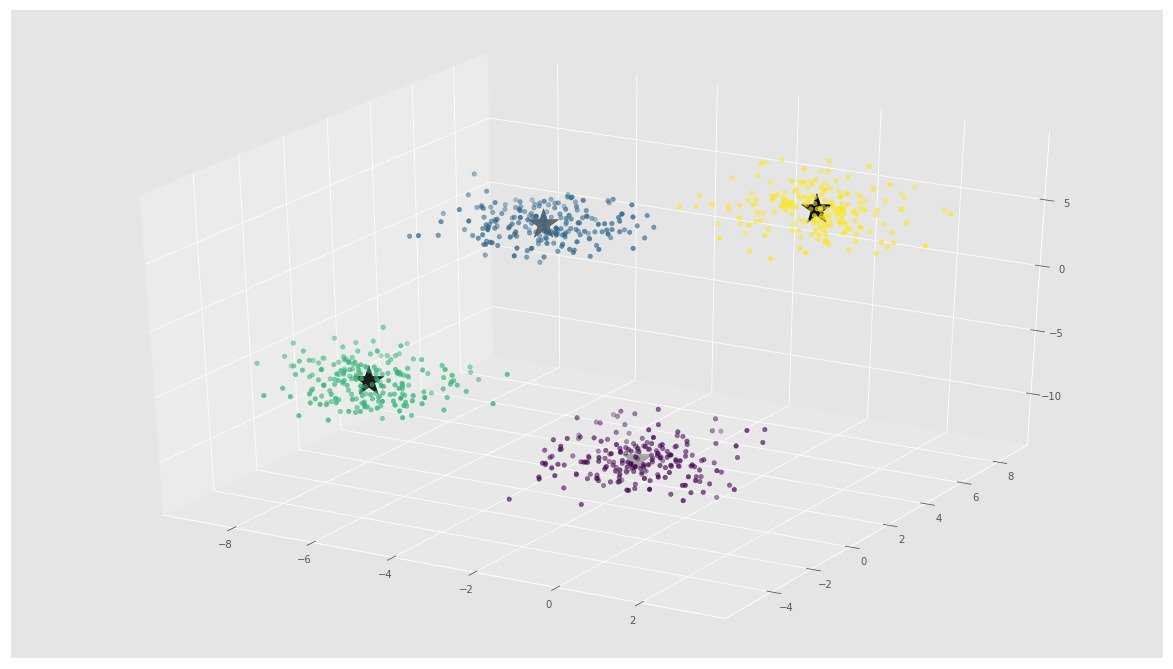
ax.scatter(C[:, 0], C[:, 1], C[:, 2], marker=’*’, c=’#050505′, s=1000)

در تصویر بالا، می‌توان ۴ خوشه و مرکزوارهای آن‌ها را که به صورت ستاره مشخص شده‌اند مشاهده کرد. استفاده از Scikit-Learn برای پیاده‌سازی الگوریتم K-Means بسیار ساده است.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش خوشه بندی K میانگین (K-Means) با نرم افزار SPSS
• مجموعه آموزش‌های یادگیری ماشین و بازشناسی الگو
• پیاده سازی الگوریتم های یادگیری ماشین با پایتون و R — به زبان ساده
• خوشه بندی k میانگین (k-means Clustering) — به همراه کدهای R

منبع [+]