الگوریتم رنگ آمیزی نرده — راهنمای کاربردی

در این مطلب، روش نوشتن برنامه الگوریتم رنگ آمیزی نرده (Painting Fence Algorithm) بیان شده و پیاده‌سازی آن در زبان‌های برنامه‌نویسی گوناگون انجام شده است.

الگوریتم رنگ آمیزی نرده

نرده‌ای با n میله و k رنگ داده شده است. هدف پیدا کردن تعداد راه‌هایی است که حداکثر دو میله مجاور، دارای یک رنگ مشابه باشند. با توجه به اینکه پاسخ ممکن است عدد بسیار بزرگی باشد، به پیمانه ۷+۹^۱۰ بازگردانده می‌شود. مثال‌های زیر در این راستا قابل توجه است.

Input : n = 2 k = 4
Output : 16
We have 4 colors and 2 posts.
Ways when both posts have same color : 4
Ways when both posts have diff color :
۴*(choices for 1st post) * 3(choices for
۲nd post) = 12

Input : n = 3 k = 2
Output : 6

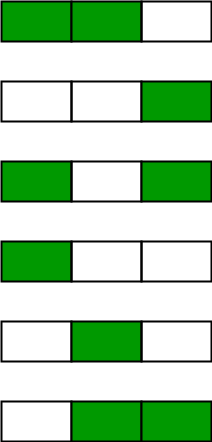
در تصاویر زیر، شش راه برای رنگ کردن سه میله با استفاده از دو رنگ، نمایش داده شده است.

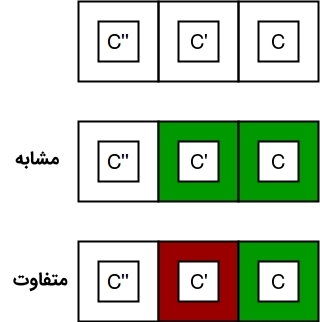
تصویر زیر مفروض است که در آن، c’‎ ،c و c”‎ رنگ‌های مربوط به میله‌های i-1 ،i و i -2 است.

با توجه به قید موجود در برنامه، به طور هم‌زمان امکان c = c’ = c”‎ وجود ندارد، بنابراین c’ != c‎ یا c” != c یا هر دو این گزاره‌ها می‌تواند صادق باشد. k-1 حالت ممکن برای c’ != c و k – ۱ حالت برای c” != c وجود دارد. شبه کد الگوریتم رنگ‌آمیزی نرده در ادامه آمده است.

diff = no of ways when color of last
two posts is different
same = no of ways when color of last
two posts is same
total ways = diff + sum

for n = 1
diff = k, same = 0
total = k

for n = 2
diff = k * (k-1) //k choices for
first post, k-1 for next
same = k //k choices for common
color of two posts
total = k + k * (k-1)

for n = 3
diff = [k + k * (k-1)] * (k-1)
(k-1) choices for 3rd post
to not have color of 2nd
post.
same = k * (k-1)
c” != c, (k-1) choices for it

Hence we deduce that,
total[i] = same[i] + diff[i]
same[i] = diff[i-1]
diff[i] = (diff[i-1] + diff[i-2]) * (k-1)
= total[i-1] * (k-1)

در ادامه، پیاده‌سازی الگوریتم بالا در زبان‌های برنامه‌نویسی گوناگون انجام شده است.

برنامه الگوریتم رنگ آمیزی نرده در ++C

// C++ program for Painting Fence Algorithm 
#include<bits/stdc++.h> 
using namespace std; 
  
// Returns count of ways to color k posts 
// using k colors 
long countWays(int n, int k) 
{ 
    // To store results for subproblems 
    long dp[n + 1]; 
    memset(dp, 0, sizeof(dp)); 
    int mod = 1000000007; 
  
    // There are k ways to color first post 
    dp[1] = k; 
  
    // There are 0 ways for single post to 
    // violate (same color_ and k ways to 
    // not violate (different color) 
    int same = 0, diff = k; 
  
    // Fill for 2 posts onwards 
    for (int i = 2; i <= n; i++) 
    { 
        // Current same is same as previous diff 
        same = diff; 
  
        // We always have k-1 choices for next post 
        diff = dp[i-1] * (k-1); 
        diff = diff % mod; 
  
        // Total choices till i. 
        dp[i] = (same + diff) % mod; 
    } 
  
    return dp[n]; 
} 
  
// Driver code 
int main() 
{ 
    int n = 3, k = 2; 
    cout << countWays(n, k) << endl; 
    return 0; 
}

برنامه الگوریتم رنگ آمیزی نرده در جاوا

// Java program for Painting Fence Algorithm 
import java.util.*; 
  
class GfG  
{ 
  
// Returns count of ways to color k posts 
// using k colors 
static long countWays(int n, int k) 
{ 
    // To store results for subproblems 
    long dp[] = new long[n + 1]; 
    Arrays.fill(dp, 0); 
    int mod = 1000000007; 
  
    // There are k ways to color first post 
    dp[1] = k; 
  
    // There are 0 ways for single post to 
    // violate (same color_ and k ways to 
    // not violate (different color) 
    int same = 0, diff = k; 
  
    // Fill for 2 posts onwards 
    for (int i = 2; i <= n; i++) 
    { 
        // Current same is same as previous diff 
        same = diff; 
  
        // We always have k-1 choices for next post 
        diff = (int) (dp[i-1] * (k-1)); 
        diff = diff % mod; 
  
        // Total choices till i. 
        dp[i] = (same + diff) % mod; 
    } 
  
    return dp[n]; 
} 
  
    // Driver code 
    public static void main(String[] args) 
    { 
        int n = 3, k = 2; 
        System.out.println(countWays(n, k)); 
    } 
} 
  
// This code contributed by Rajput-Ji

بهینه‌سازی فضایی الگوریتم رنگ‌آمیزی نرده

الگوریتم ارائه شده در بخش پیشین را می‌توان با استفاده از یک متغیر به جای جدول، بهینه‌سازی کرد. در ادامه، نسخه بهینه‌سازی فضایی شده از الگوریتم رنگ‌آمیزی نرده در زبان‌های برنامه‌نویسی گوناگون پیاده‌سازی شده  است.

برنامه الگوریتم رنگ آمیزی نرده با بهینه‌سازی فضایی در ++C

// C++ program for Painting Fence Algorithm 
#include<bits/stdc++.h> 
using namespace std; 
  
// Returns count of ways to color k posts 
// using k colors 
long countWays(int n, int k) 
{ 
    // There are k ways to color first post 
    long total = k; 
    int mod = 1000000007; 
  
    // There are 0 ways for single post to 
    // violate (same color_ and k ways to 
    // not violate (different color) 
    int same = 0, diff = k; 
  
    // Fill for 2 posts onwards 
    for (int i = 2; i <= n; i++) 
    { 
        // Current same is same as previous diff 
        same = diff; 
  
        // We always have k-1 choices for next post 
        diff = total * (k-1); 
        diff = diff % mod; 
  
        // Total choices till i. 
        total = (same + diff) % mod; 
    } 
  
    return total; 
} 
  
// Driver code 
int main() 
{ 
    int n = 3, k = 2; 
    cout << countWays(n, k) << endl; 
    return 0; 
}

برنامه الگوریتم رنگ آمیزی نرده با بهینه‌سازی فضایی در جاوا

// Java program for Painting Fence Algorithm 
class GFG  
{ 
      
// Returns count of ways to color k posts 
// using k colors 
static long countWays(int n, int k) 
{ 
    // There are k ways to color first post 
    long total = k; 
    int mod = 1000000007; 
  
    // There are 0 ways for single post to 
    // violate (same color_ and k ways to 
    // not violate (different color) 
    int same = 0, diff = k; 
  
    // Fill for 2 posts onwards 
    for (int i = 2; i <= n; i++) 
    { 
        // Current same is same as previous diff 
        same = diff; 
  
        // We always have k-1 choices for next post 
        diff = (int)total * (k - 1); 
        diff = diff % mod; 
  
        // Total choices till i. 
        total = (same + diff) % mod; 
    } 
    return total; 
} 
  
// Driver code 
public static void main(String[] args) 
{ 
    int n = 3, k = 2; 
    System.out.println(countWays(n, k)); 
} 
} 
  
//This code is contributed by Mukul Singh

# Python3 program for Painting  
# Fence Algorithm  
  
# Returns count of ways to color  
# k posts using k colors  
def countWays(n, k) : 
  
    # There are k ways to color first post  
    total = k 
    mod = 1000000007
  
    # There are 0 ways for single post to  
    # violate (same color_ and k ways to  
    # not violate (different color)  
    same, diff = 0, k 
  
    # Fill for 2 posts onwards  
    for i in range(2, n + 1) : 
          
        # Current same is same as  
        # previous diff  
        same = diff  
  
        # We always have k-1 choices  
        # for next post  
        diff = total * (k - 1)  
        diff = diff % mod  
  
        # Total choices till i.  
        total = (same + diff) % mod  
      
    return total 
  
# Driver code  
if __name__ == "__main__" : 
  
    n, k = 3, 2
    print(countWays(n, k))  
  
# This code is contributed by Ryuga

// C# program for Painting Fence Algorithm  
using System;  
  
class GFG  
{  
    // Returns count of ways to color k posts  
    // using k colors  
    static long countWays(int n, int k)  
    {  
        // There are k ways to color first post  
        long total = k;  
        int mod = 1000000007;  
      
        // There are 0 ways for single post to  
        // violate (same color_ and k ways to  
        // not violate (different color)  
        long same = 0, diff = k;  
      
        // Fill for 2 posts onwards  
        for (int i = 2; i <= n; i++)  
        {  
            // Current same is same as previous diff  
            same = diff;  
      
            // We always have k-1 choices for next post  
            diff = total * (k - 1);  
            diff = diff % mod;  
      
            // Total choices till i.  
            total = (same + diff) % mod;  
        }  
      
        return total;  
    }  
      
    // Driver code 
    static void Main()  
    {  
        int n = 3, k = 2;  
        Console.Write(countWays(n, k));  
    } 
} 
  
//This code is contributed by DrRoot_

<?php  
// PHP program for Painting Fence Algorithm 
  
// Returns count of ways to color k  
// posts using k colors 
function countWays($n, $k) 
{ 
    // There are k ways to color first post 
    $total = $k; 
    $mod = 1000000007; 
  
    // There are 0 ways for single post to 
    // violate (same color_ and k ways to 
    // not violate (different color) 
    $same = 0; 
    $diff = $k; 
  
    // Fill for 2 posts onwards 
    for ($i = 2; $i <= $n; $i++) 
    { 
        // Current same is same as previous diff 
        $same = $diff; 
  
        // We always have k-1 choices for next post 
        $diff = $total * ($k - 1); 
        $diff = $diff % $mod; 
  
        // Total choices till i. 
        $total = ($same + $diff) % $mod; 
    } 
  
    return $total; 
} 
  
// Driver code 
$n = 3; 
$k = 2; 
echo countWays($n, $k) . "\n"; 
  
// This code is contributed by ita_c 
?>

۶

(No Ratings Yet)

Loading...

پاسخی بگذارید لغو پاسخ

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *

دیدگاه

نام *

ایمیل *

وب‌سایت

ذخیره نام، ایمیل و وبسایت من در مرورگر برای زمانی که دوباره دیدگاهی می‌نویسم.