مسیر اویلری (Eulerian Path) مسیری درگراف است که در آن، هر رأس از گراف، دقیقا یک‌بار مشاهده می‌شود. «دور اویلری» (Eulerian Circuit) یک مسیر اویلری است که با یک رأس شرع و با همان رأس نیز تمام می‌شود. یک گراف را گراف اویلری می‌گویند اگر دارای دور اویلری باشد. در این مطلب، به بررسی دور اویلری در گراف جهت‌دار پرداخته می‌شود. برای مثال، گراف زیر دارای دور اویلری {۱, ۰, ۳, ۴, ۰, ۲, ۱} است.

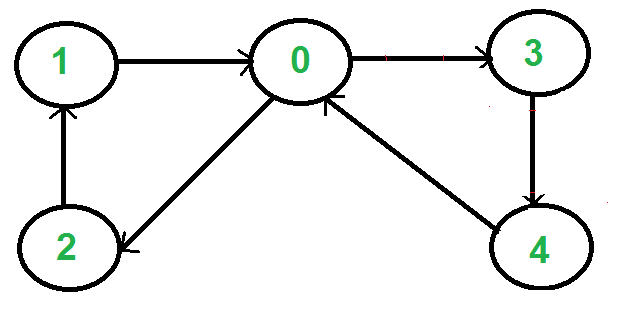
روش بررسی اویلری بودن یک گراف جهت‌دار

یک گراف جهت‌دار در صورت صدق کردن در شرط‌های زیر، اویلری محسوب می‌شود.

1. همه رأس‌ها با درجه غیر صفر متعلق به یک مولفه قویا متصل مجرد باشند.
2. درجه ورود برای هر رأس با درجه خروج برای آن رآس دقیقا برابر باشد.

می‌توان یک مولفه متصل به صورت مجرد را با استفاده از «الگوریتم ساده مبتنی بر جستجوی اول عمق کساراجو» (Kosaraju’s DFS Based Simple Algorithm) شناسایی کرد. برای مقایسه درجه ورودی و خروجی، نیاز به ذخیره‌سازی درجه ورودی و خروجی برای همه رأس‌ها است. درجه خروجی را می‌توان با استفاده از اندازه لیست مجاورت نیز به دست آورد. درج ورودی را می‌توان با ساخت یک آرایه با اندازه‌ای مشابه با اندازه رأس‌ها ذخیره‌سازی کرد. در ادامه، پیاده‌سازی رویکرد بیان شده در زبان‌های برنامه‌نویسی «سی‌پلاس‌پلاس» (++C)، «جاوا» (Java) و «پایتون» (Python) انجام شده است.

پیاده‌سازی برنامه تشخیص دور اویلری در گراف جهت‌دار با ++C

// A C++ program to check if a given directed graph is Eulerian or not 
#include<iostream> 
#include <list> 
#define CHARS 26 
using namespace std; 
  
// A class that represents an undirected graph 
class Graph 
{ 
    int V;    // No. of vertices 
    list<int> *adj;    // A dynamic array of adjacency lists 
    int *in; 
public: 
    // Constructor and destructor 
    Graph(int V); 
    ~Graph()   { delete [] adj; delete [] in; } 
  
    // function to add an edge to graph 
    void addEdge(int v, int w) { adj[v].push_back(w);  (in[w])++; } 
  
    // Method to check if this graph is Eulerian or not 
    bool isEulerianCycle(); 
  
    // Method to check if all non-zero degree vertices are connected 
    bool isSC(); 
  
    // Function to do DFS starting from v. Used in isConnected(); 
    void DFSUtil(int v, bool visited[]); 
  
    Graph getTranspose(); 
}; 
  
Graph::Graph(int V) 
{ 
    this->V = V; 
    adj = new list<int>[V]; 
    in = new int[V]; 
    for (int i = 0; i < V; i++) 
       in[i] = 0; 
} 
  
/* This function returns true if the directed graph has a eulerian 
   cycle, otherwise returns false  */
bool Graph::isEulerianCycle() 
{ 
    // Check if all non-zero degree vertices are connected 
    if (isSC() == false) 
        return false; 
  
    // Check if in degree and out degree of every vertex is same 
    for (int i = 0; i < V; i++) 
        if (adj[i].size() != in[i]) 
            return false; 
  
    return true; 
} 
  
// A recursive function to do DFS starting from v 
void Graph::DFSUtil(int v, bool visited[]) 
{ 
    // Mark the current node as visited and print it 
    visited[v] = true; 
  
    // Recur for all the vertices adjacent to this vertex 
    list<int>::iterator i; 
    for (i = adj[v].begin(); i != adj[v].end(); ++i) 
        if (!visited[*i]) 
            DFSUtil(*i, visited); 
} 
  
// Function that returns reverse (or transpose) of this graph 
// This function is needed in isSC() 
Graph Graph::getTranspose() 
{ 
    Graph g(V); 
    for (int v = 0; v < V; v++) 
    { 
        // Recur for all the vertices adjacent to this vertex 
        list<int>::iterator i; 
        for(i = adj[v].begin(); i != adj[v].end(); ++i) 
        { 
            g.adj[*i].push_back(v); 
            (g.in[v])++; 
        } 
    } 
    return g; 
} 
  
// This function returns true if all non-zero degree vertices of  
// graph are strongly connected (Please refer  
// https://www.geeksforgeeks.org/connectivity-in-a-directed-graph/ ) 
bool Graph::isSC() 
{ 
    // Mark all the vertices as not visited (For first DFS) 
    bool visited[V]; 
    for (int i = 0; i < V; i++) 
        visited[i] = false; 
  
    // Find the first vertex with non-zero degree 
    int n; 
    for (n = 0; n < V; n++) 
        if (adj[n].size() > 0) 
          break; 
  
    // Do DFS traversal starting from first non zero degrees vertex. 
    DFSUtil(n, visited); 
  
     // If DFS traversal doesn't visit all vertices, then return false. 
    for (int i = 0; i < V; i++) 
        if (adj[i].size() > 0 && visited[i] == false) 
              return false; 
  
    // Create a reversed graph 
    Graph gr = getTranspose(); 
  
    // Mark all the vertices as not visited (For second DFS) 
    for (int i = 0; i < V; i++) 
        visited[i] = false; 
  
    // Do DFS for reversed graph starting from first vertex. 
    // Staring Vertex must be same starting point of first DFS 
    gr.DFSUtil(n, visited); 
  
    // If all vertices are not visited in second DFS, then 
    // return false 
    for (int i = 0; i < V; i++) 
        if (adj[i].size() > 0 && visited[i] == false) 
             return false; 
  
    return true; 
} 
  
// Driver program to test above functions 
int main() 
{ 
    // Create a graph given in the above diagram 
    Graph g(5); 
    g.addEdge(1, 0); 
    g.addEdge(0, 2); 
    g.addEdge(2, 1); 
    g.addEdge(0, 3); 
    g.addEdge(3, 4); 
    g.addEdge(4, 0); 
  
    if (g.isEulerianCycle()) 
       cout << "Given directed graph is eulerian n"; 
    else
       cout << "Given directed graph is NOT eulerian n"; 
    return 0;

پیاده‌سازی برنامه تشخیص دور اویلری در گراف جهت‌دار با جاوا

// A Java program to check if a given directed graph is Eulerian or not 
  
// A class that represents an undirected graph 
import java.io.*; 
import java.util.*; 
import java.util.LinkedList; 
  
// This class represents a directed graph using adjacency list 
class Graph 
{ 
    private int V;   // No. of vertices 
    private LinkedList<Integer> adj[];//Adjacency List 
    private int in[];            //maintaining in degree 
  
    //Constructor 
    Graph(int v) 
    { 
        V = v; 
        adj = new LinkedList[v]; 
        in = new int[V]; 
        for (int i=0; i<v; ++i) 
        { 
            adj[i] = new LinkedList(); 
            in[i]  = 0; 
        } 
    } 
  
    //Function to add an edge into the graph 
    void addEdge(int v,int w) 
    { 
        adj[v].add(w); 
        in[w]++; 
    } 
  
    // A recursive function to print DFS starting from v 
    void DFSUtil(int v,Boolean visited[]) 
    { 
        // Mark the current node as visited 
        visited[v] = true; 
  
        int n; 
  
        // Recur for all the vertices adjacent to this vertex 
        Iterator<Integer> i =adj[v].iterator(); 
        while (i.hasNext()) 
        { 
            n = i.next(); 
            if (!visited[n]) 
                DFSUtil(n,visited); 
        } 
    } 
  
    // Function that returns reverse (or transpose) of this graph 
    Graph getTranspose() 
    { 
        Graph g = new Graph(V); 
        for (int v = 0; v < V; v++) 
        { 
            // Recur for all the vertices adjacent to this vertex 
            Iterator<Integer> i = adj[v].listIterator(); 
            while (i.hasNext()) 
            { 
                g.adj[i.next()].add(v); 
                (g.in[v])++; 
            } 
        } 
        return g; 
    } 
  
    // The main function that returns true if graph is strongly 
    // connected 
    Boolean isSC() 
    { 
        // Step 1: Mark all the vertices as not visited (For 
        // first DFS) 
        Boolean visited[] = new Boolean[V]; 
        for (int i = 0; i < V; i++) 
            visited[i] = false; 
  
        // Step 2: Do DFS traversal starting from the first vertex. 
        DFSUtil(0, visited); 
  
        // If DFS traversal doesn't visit all vertices, then return false. 
        for (int i = 0; i < V; i++) 
            if (visited[i] == false) 
                return false; 
  
        // Step 3: Create a reversed graph 
        Graph gr = getTranspose(); 
  
        // Step 4: Mark all the vertices as not visited (For second DFS) 
        for (int i = 0; i < V; i++) 
            visited[i] = false; 
  
        // Step 5: Do DFS for reversed graph starting from first vertex. 
        // Staring Vertex must be same starting point of first DFS 
        gr.DFSUtil(0, visited); 
  
        // If all vertices are not visited in second DFS, then 
        // return false 
        for (int i = 0; i < V; i++) 
            if (visited[i] == false) 
                return false; 
  
        return true; 
    } 
  
    /* This function returns true if the directed graph has a eulerian 
       cycle, otherwise returns false  */
    Boolean isEulerianCycle() 
    { 
        // Check if all non-zero degree vertices are connected 
        if (isSC() == false) 
            return false; 
  
        // Check if in degree and out degree of every vertex is same 
        for (int i = 0; i < V; i++) 
            if (adj[i].size() != in[i]) 
                return false; 
  
        return true; 
    } 
  
    public static void main (String[] args) throws java.lang.Exception 
    { 
        Graph g = new Graph(5); 
        g.addEdge(1, 0); 
        g.addEdge(0, 2); 
        g.addEdge(2, 1); 
        g.addEdge(0, 3); 
        g.addEdge(3, 4); 
        g.addEdge(4, 0); 
  
        if (g.isEulerianCycle()) 
            System.out.println("Given directed graph is eulerian "); 
        else
            System.out.println("Given directed graph is NOT eulerian "); 
    } 
} 
//This code is contributed by Aakash Hasija

پیاده‌سازی برنامه تشخیص دوراویلری در گراف جهت‌دار با پایتون

# A Python program to check if a given  
# directed graph is Eulerian or not 
  
from collections import defaultdict 
  
class Graph(): 
  
    def __init__(self, vertices): 
        self.V = vertices 
        self.graph = defaultdict(list) 
        self.IN = [0] * vertices 
  
    def addEdge(self, v, u): 
  
        self.graph[v].append(u) 
        self.IN[u] += 1
  
    def DFSUtil(self, v, visited): 
        visited[v] = True
        for node in self.graph[v]: 
            if visited[node] == False: 
                self.DFSUtil(node, visited) 
  
    def getTranspose(self): 
        gr = Graph(self.V) 
  
        for node in range(self.V): 
            for child in self.graph[node]: 
                gr.addEdge(child, node) 
  
        return gr 
  
    def isSC(self): 
        visited = [False] * self.V 
  
        v = 0
        for v in range(self.V): 
            if len(self.graph[v]) > 0: 
                break
  
        self.DFSUtil(v, visited) 
  
        # If DFS traversal doesn't visit all  
        # vertices, then return false. 
        for i in range(self.V): 
            if visited[i] == False: 
                return False
  
        gr = self.getTranspose() 
  
        visited = [False] * self.V 
        gr.DFSUtil(v, visited) 
  
        for i in range(self.V): 
            if visited[i] == False: 
                return False
  
        return True
  
    def isEulerianCycle(self): 
  
        # Check if all non-zero degree vertices  
        # are connected 
        if self.isSC() == False: 
            return False
  
        # Check if in degree and out degree of  
        # every vertex is same 
        for v in range(self.V): 
            if len(self.graph[v]) != self.IN[v]: 
                return False
  
        return True
  
  
g = Graph(5); 
g.addEdge(1, 0); 
g.addEdge(0, 2); 
g.addEdge(2, 1); 
g.addEdge(0, 3); 
g.addEdge(3, 4); 
g.addEdge(4, 0); 
if g.isEulerianCycle(): 
   print "Given directed graph is eulerian"; 
else: 
   print "Given directed graph is NOT eulerian"; 
  
# This code is contributed by Divyanshu Mehta

خروجی قطعه کدهای بالا به صورت زیر است.

Given directed graph is eulerian

پیچیدگی زمانی پیاده‌سازی بالا از درجه (O(V + E است؛ زیرا الگوریتم کساراجو (O(V + E زمان می‌برد. پس از اجرای الگوریتم کساراجو، همه رأس‌ها پیمایش و رأس‌های ورودی و خروجی با یکدیگر مقایسه می‌شوند که این کار از درجه (O(V زمان می‌برد.

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• معرفی منابع آموزش ویدئویی هوش مصنوعی به زبان فارسی و انگلیسی
• زبان برنامه‌نویسی پایتون (Python) — از صفر تا صد
• آموزش ساختمان داده — مجموعه مقالات جامع وبلاگ فرادرس

منبع [+]