مسئله پوشش رأس ها — راهنمای کاربردی
پوشش رأس در یک گراف غیرجهتدار، یک زیرمجموعه از رأسهای آن است که برای هر رأس (u, v) از گراف، u یا v در پوشش راس قرار دارد. با وجود آنکه نام این مسئله Vertex Cover است، مجموعه همه یالها در گراف داده شده را پوشش میدهد. یک گراف غیر جهتدار داده شده است، مسئله پوشش رأس، در واقع مسئله پیدا کردن پوشش رأس کمینه است. مسئله پوشش رأس به عنوان یک مسئله NP-کامل نیز شناخته شده است، زیرا هیچ راهکاری از درجه زمانی دوجملهای برای حل آن وجود ندارد، مگر آنکه P = NP. الگریتمهای از درجه زمانی تقریبا دوجملهای برای حل مسئله وجود دارد. در ادامه، یک الگوریتم تقریبی ارائه شده است.
الگوریتم تقریبی برای حل مسئله پوشش رأس
- مقداردهی اولیه به صورت {}
- یک مجموعه از یالها را در گراف در نظر بگیر. فرض کن که مجموعه E باشد.
- تا هنگامی که E خالی است، اقدامات زیر را انجام بده:
- یک یال دلخواه (u, v) را از مجموعه E انتخاب و ‘u’ و ‘v’ را به نتیجه اضافه کن.
- همه رأسها را از E حذف کن که میتواند u یا v باشد.
- نتیجه را بازگردان.
نمودار زیر، روند اجرای الگوریتم تقریبی زیر را نشان میدهد.
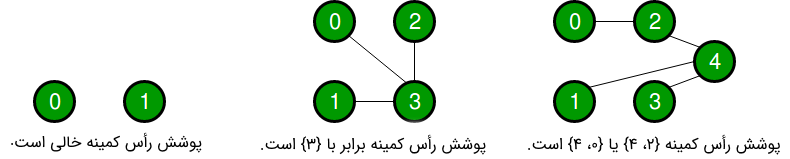
پرسشی که در این وهله مطرح میشود این است که عملکرد الگوریتم بالا چقدر خوب است؟ در پاسخ به این پرسش میتوان اثبات کرد که الگوریتم تخمین بالا هیچ وقت پوشش رأسی را که سایز آن بیش از دو برابر پوشش رأس کمینه باشد، پیدا نمیکند. در ادامه، پیادهسازی الگوریتم بالا در زبانهای برنامهنویسی «سیپلاسپلاس» (++C) و «جاوا» (Java) انجام شده است.
پیادهسای الگوریتم حل مسئله پوشش رأسها در ++C
// Program to print Vertex Cover of a given undirected graph
#include<iostream>
#include <list>
using namespace std;
// This class represents a undirected graph using adjacency list
class Graph
{
int V; // No. of vertices
list<int> *adj; // Pointer to an array containing adjacency lists
public:
Graph(int V); // Constructor
void addEdge(int v, int w); // function to add an edge to graph
void printVertexCover(); // prints vertex cover
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w); // Add w to v’s list.
adj[w].push_back(v); // Since the graph is undirected
}
// The function to print vertex cover
void Graph::printVertexCover()
{
// Initialize all vertices as not visited.
bool visited[V];
for (int i=0; i<V; i++)
visited[i] = false;
list<int>::iterator i;
// Consider all edges one by one
for (int u=0; u<V; u++)
{
// An edge is only picked when both visited[u] and visited[v]
// are false
if (visited[u] == false)
{
// Go through all adjacents of u and pick the first not
// yet visited vertex (We are basically picking an edge
// (u, v) from remaining edges.
for (i= adj[u].begin(); i != adj[u].end(); ++i)
{
int v = *i;
if (visited[v] == false)
{
// Add the vertices (u, v) to the result set.
// We make the vertex u and v visited so that
// all edges from/to them would be ignored
visited[v] = true;
visited[u] = true;
break;
}
}
}
}
// Print the vertex cover
for (int i=0; i<V; i++)
if (visited[i])
cout << i << " ";
}
// Driver program to test methods of graph class
int main()
{
// Create a graph given in the above diagram
Graph g(7);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 3);
g.addEdge(3, 4);
g.addEdge(4, 5);
g.addEdge(5, 6);
g.printVertexCover();
return 0;پیادهسای الگوریتم حل مسئله پوشش رأسها در جاوا
// Java Program to print Vertex Cover of a given undirected graph
import java.io.*;
import java.util.*;
import java.util.LinkedList;
// This class represents an undirected graph using adjacency list
class Graph
{
private int V; // No. of vertices
// Array of lists for Adjacency List Representation
private LinkedList<Integer> adj[];
// Constructor
Graph(int v)
{
V = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i)
adj[i] = new LinkedList();
}
//Function to add an edge into the graph
void addEdge(int v, int w)
{
adj[v].add(w); // Add w to v's list.
adj[w].add(v); //Graph is undirected
}
// The function to print vertex cover
void printVertexCover()
{
// Initialize all vertices as not visited.
boolean visited[] = new boolean[V];
for (int i=0; i<V; i++)
visited[i] = false;
Iterator<Integer> i;
// Consider all edges one by one
for (int u=0; u<V; u++)
{
// An edge is only picked when both visited[u]
// and visited[v] are false
if (visited[u] == false)
{
// Go through all adjacents of u and pick the
// first not yet visited vertex (We are basically
// picking an edge (u, v) from remaining edges.
i = adj[u].iterator();
while (i.hasNext())
{
int v = i.next();
if (visited[v] == false)
{
// Add the vertices (u, v) to the result
// set. We make the vertex u and v visited
// so that all edges from/to them would
// be ignored
visited[v] = true;
visited[u] = true;
break;
}
}
}
}
// Print the vertex cover
for (int j=0; j<V; j++)
if (visited[j])
System.out.print(j+" ");
}
// Driver method
public static void main(String args[])
{
// Create a graph given in the above diagram
Graph g = new Graph(7);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 3);
g.addEdge(3, 4);
g.addEdge(4, 5);
g.addEdge(5, 6);
g.printVertexCover();
}
}
// This code is contributed by Aakash Hasijaپیچیدگی زمانی الگوریتم بالا از درجه (O(V + E است. همانطور که پیش از این نیز بیان شد، روش بیان شده در بالا یک روش تقریبی است. این مسئله، یک مسئله NP کامل محسوب میشود و امکان حل آن از درجه دو جملهای تنها برای «گرافهای دو بخشی» (Bipartite Graph) و «درختی» (Tree Graph) قابل انجام است.
اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای برنامهنویسی
- آموزش ساختمان دادهها
- مجموعه آموزشهای ساختمان داده و طراحی الگوریتم
- معرفی منابع آموزش ویدئویی هوش مصنوعی به زبان فارسی و انگلیسی
- زبان برنامهنویسی پایتون (Python) — از صفر تا صد
- آموزش ساختمان داده — مجموعه مقالات جامع وبلاگ فرادرس
مجموعه: برنامه نویسی, ریاضیات کاربردی, مهندسی کامپیوتر برچسب ها: minimum vertex cover, Vertex cover, الگوریتم های گراف, پوشش راس کمینه, رأس پوششی, گراف, مسئله پوشش راس ها, مسائل گراف, مساله پوشش راس ها




 (No Ratings Yet)
(No Ratings Yet)