در این مطلب، روش نوشتن برنامه محاسبه «فاصله همرد» (Hammered Distance) بین N نقطه در یک صفحه دوبُعدی بیان شده است.

برنامه محاسبه فاصله همرد بین N نقطه

n نقطه در یک فضای دوبُعدی به صورت Xi, Yi داده شده است که این n نقطه را توصیف می‌کنند. هدف، محاسبه فاصله همرد بین n نقطه است. شایان توجه است ک فاصله همرد، مجموع مربعات کوتاه‌ترین فاصله بین هر جفت از نقاط است. مثال زیر برای درک بهتر این مطلب، قابل توجه است.

Input: n = 3
۰ ۱
۰ ۰
۱ ۰
Output: 4

Input: n = 4
۱ ۰
۲ ۰
۳ ۰
۴ ۰

Output: 20

راهکار پایه برای محاسبه فاصله همرد بین N نقطه

هدف، محاسبه مجموعه مربعات کوتاه‌ترین مسیر، بین همه جفت نقاط موجود است. بنابراین، می‌توان هر جفت ممکنی از نقاط را دریافت و مجموع مربعات فواصل را محاسبه کرد. شبه کد لازم برای انجام این کار، در ادامه بیان شده است.

// Pseudo code to find hammered-distance using above approach.
//this will store hammered distance
Distance=0
for(int i=0;i<n;i++)
{
    for(int j=i+1;j<n;j++)
    {
         //shortest distance between point i and j.
         Distance+=(x[i]-x[j])^2+(y[i]-y[j])^2
     }
}

پیچیدگی زمانی این روش، از درجه O(n^2)‎ است.

راهکار بهینه‌تر برای محاسبه فاصله همرد بین N نقطه

مسئله را می‌توان با پیچیدگی زمانی O(N)‎ حل کرد.

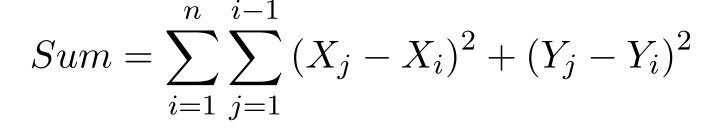
این مسئله را می‌توان برای مختصات‌های x و y حل کرد. برای X:

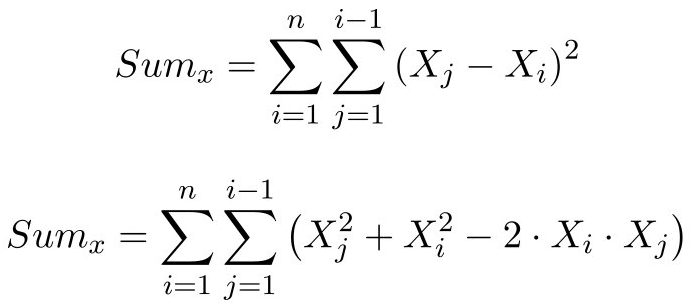
اکنون، می‌توان بخش مجموع را بسط داد و این معادله را به صورت زیر نوشت.

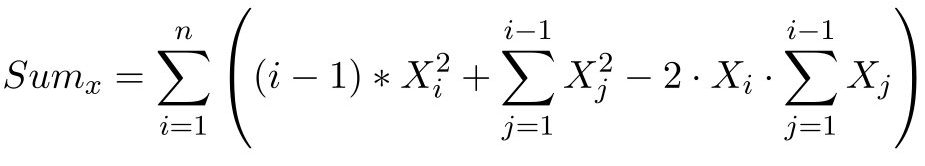
مجموع تجمعی مربعات نقاط تا i-1 به صورت زیر است.

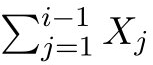
بنابراین، می‌توان آن را در زمان خطی محاسبه کرد. به طور مشابه، این مورد می‌تواند زمان محاسبه شده باشد.

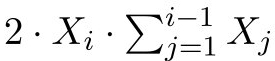
در ادامه، پیاده‌سازی رویکرد بالا ارائه شده است.

پیاده‌سازی برنامه محاسبه فاصله همرد بین N نقطه در ++C

// C++ implementation of above approach 
#include <bits/stdc++.h> 
#define ll long long int 
using namespace std; 
  
// Function calculate cummalative sum 
// of x, y, x^2, y^2 coordinates. 
ll cumm(vector<ll>& x, vector<ll>& y, 
        vector<ll>& cummx, vector<ll>& cummy, 
        vector<ll>& cummx2, vector<ll>& cummy2, ll n) 
{ 
    for (int i = 1; i <= n; i++) { 
        cummx[i] = cummx[i - 1] + x[i]; 
        cummy[i] = cummy[i - 1] + y[i]; 
        cummx2[i] = cummx2[i - 1] + x[i] * x[i]; 
        cummy2[i] = cummy2[i - 1] + y[i] * y[i]; 
    } 
} 
  
// Function ot calculate the hammered distance 
int calHammeredDistance(int n, vector<ll>& x, vector<ll>& y) 
{ 
    // cummx conatins cummulative sum of x 
    // cummy conatins cummulative sum of y 
    vector<ll> cummx(n + 1, 0), cummy(n + 1, 0); 
  
    // cummx2 conatins cummulative sum of x^2 
    // cummy2 conatins cummulative sum of y^2 
    vector<ll> cummx2(n + 1, 0), cummy2(n + 1, 0); 
  
    // calculate cummalative of x 
    //, y, x^2, y^2, because these terms 
    // required in formula to reduce complexity. 
  
    // this function calculate all required terms. 
    cumm(x, y, cummx, cummy, cummx2, cummy2, n); 
  
    // hdx calculate hammer distance for x coordinate 
    // hdy calculate hammer distance for y coordinate 
    ll hdx = 0, hdy = 0; 
  
    for (int i = 1; i <= n; i++) { 
  
        // came from formula describe in explanation 
        hdx += (i - 1) * x[i] * x[i] + cummx2[i - 1] 
               - ۲ * x[i] * cummx[i - 1]; 
  
        // came from formula describe in explanation 
        hdy += (i - 1) * y[i] * y[i] + cummy2[i - 1] 
               - ۲ * y[i] * cummy[i - 1]; 
    } 
  
    // total is the sum of both x and y. 
    ll total = hdx + hdy; 
    return total; 
} 
  
// Driver code 
int main() 
{ 
    // number of points 
    int n = 3; 
  
    // x contains the x coordinates 
    // y conatins the y coordinates 
    vector<ll> x(n + 1), y(n + 1); 
    x = { 0, 0, 1 }; 
    y = { 1, 0, 0 }; 
  
    cout << calHammeredDistance(n, x, y); 
  
    return 0; 
}

پیاده‌سازی برنامه محاسبه فاصله همرد بین N نقطه در پایتون

# Python3 implementation of the  
# above approach  
  
# Function calculate cummalative sum  
# of x, y, x^2, y^2 coordinates.  
def cumm(x, y, cummx, cummy,  
               cummx2, cummy2, n):  
  
    for i in range(1, n+1):  
        cummx[i] = cummx[i - 1] + x[i]  
        cummy[i] = cummy[i - 1] + y[i]  
        cummx2[i] = cummx2[i - 1] + x[i] * x[i]  
        cummy2[i] = cummy2[i - 1] + y[i] * y[i]  
  
# Function ot calculate the  
# hammered distance  
def calHammeredDistance(n, x, y):  
  
    # cummx conatins cummulative sum of x  
    # cummy conatins cummulative sum of y  
    cummx = [0] * (n + 1) 
    cummy = [0] * (n + 1)  
  
    # cummx2 conatins cummulative sum of x^2  
    # cummy2 conatins cummulative sum of y^2  
    cummx2 = [0] * (n + 1) 
    cummy2 = [0] * (n + 1)  
  
    # calculate cumulative of x , y, x^2, y^2,  
    # because these terms are required in the 
    # formula to reduce complexity.  
  
    # This function calculate all required terms.  
    cumm(x, y, cummx, cummy, cummx2, cummy2, n)  
  
    # hdx calculate hammer distance for x coordinate  
    # hdy calculate hammer distance for y coordinate  
    hdx, hdy = 0, 0
  
    for i in range(1, n + 1):  
  
        # came from formula describe in explanation  
        hdx += ((i - 1) * x[i] * x[i] + cummx2[i - 1] -
                             ۲ * x[i] * cummx[i - 1]) 
  
        # came from formula describe in explanation  
        hdy += ((i - 1) * y[i] * y[i] + cummy2[i - 1] - 
                             ۲ * y[i] * cummy[i - 1]) 
      
    # total is the sum of both x and y.  
    total = hdx + hdy  
    return total  
  
# Driver Code 
if __name__ == "__main__": 
  
    # number of points  
    n = 3
  
    # x contains the x coordinates  
    # y conatins the y coordinates  
    x = [0, 0, 1, 0]  
    y = [1, 0, 0, 0]  
  
    print(calHammeredDistance(n, x, y))  
  
# This code is contributed by Rituraj Jain 

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌ نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• رنگ‌آمیزی گراف به روش حریصانه — به زبان ساده
• الگوریتم دایجسترا (Dijkstra) — از صفر تا صد
• الگوریتم پریم — به زبان ساده
• متن کاوی (Text Mining) — به زبان ساده

منبع [+]