در این مطلب، «الگوریتم اتوماتای متناهی برای جستجوی الگو» (Finite Automata Algorithm for Pattern Searching) معرفی و پیاده‌سازی آن در زبان‌های برنامه‌نویسی گوناگون شامل «سی» (C)، «سی‌پلاس‌پلاس» (++C)، «جاوا» (Java)، «پایتون» (Python) و «سی‌شارپ» (#C) انجام شده است.

الگوریتم اتوماتای متناهی برای جستجوی الگو

فرض می‌شود که یک متن txt[0..n-1] ‎ و الگوی [pat[0..m-1 داده شده است. هدف نوشتن یک جستجوی تابعی (char pat[], char txt[]‎) است که همه وقوع‌هایpat[] ‎ در txt[]‎ را چاپ می‌کند. می‌توان فرض کرد که n > m است.

مثال:

Input:  txt[] = "THIS IS A TEST TEXT"
        pat[] = "TEST"
Output: Pattern found at index 10

Input:  txt[] =  "AABAACAADAABAABA"
        pat[] =  "AABA"
Output: Pattern found at index 0
        Pattern found at index 9
        Pattern found at index 12

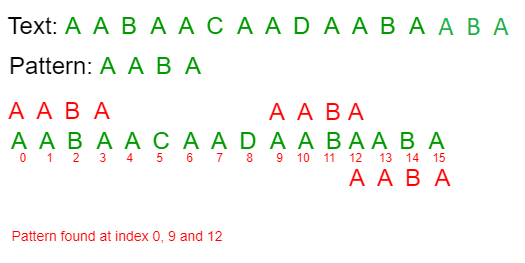
«جستجوی الگو» (Pattern Searching) یک مسئله مهم در علوم کامپیوتر است. هنگامی که جستجو برای یک رشته در فایل متنی (مانند فایل‌های ورد، لیبره‌آفیس، نوت‌پد و دیگر موارد)، «مرورگر وب» (Web Browser) یا «پایگاه داده» (Data Base) انجام می‌شود، از جستجوی الگو برای نمایش دادن نتایج جستجو استفاده می‌شود. در این مطلب، اتوماتای متناهی (Finite Automata | FA) بر پایه الگوریتم جستجوی الگو مورد استفاده قرار می‌گیرد. در الگوریتم‌های مبتنی بر FA، الگو پیش‌پردازش می‌شود و یک آرایه دوبُعدی که نشانگر یک اتوماتای متناهی است، ساخته می‌شود.

هنگامی که FA ساخته شد، جستجو کردن آسان است. در جستجو، به سادگی نیاز به شروع از اولین حالت اتوماتا و اولین کاراکتر متن است. در هر گام، کاراکتر بعدی متن در نظر گرفته می‌شود، برای حالت بعدی در FA ساخته شده جستجو و حرکت به حالت جدید انجام می‌شود. در صورت رسیدن به حالت نهایی، الگو در متن پیدا می‌شود. پیچیدگی زمانی فرایند جستجو از درجه O(n)‎ است. پیش از آنکه در مورد روش ساخت FA بحث شود، نگاهی به اتوماتای متناهی زیر که برای الگوی ACACAGA انداخته می‌شود.

 

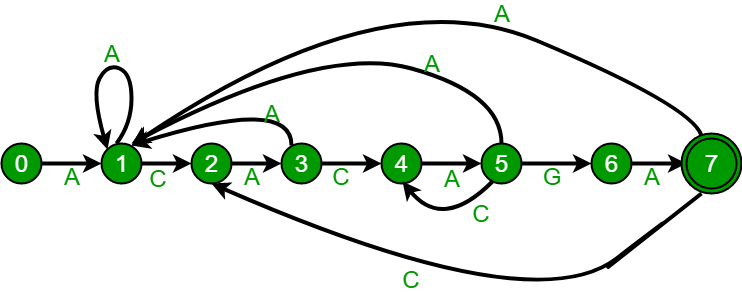
نمودارهای بالا، ارائه گرافیکی و جدولی از الگوی ACACAGA هستند. تعداد حالات در FA، برابر با M+1 است که در آن، M طول الگو محسوب می‌شود. موضوع اصلی برای ساخت اتوماتای متناهی، به دست آوردن حالت بعدی از حالت کنونی برای هر کاراکتر ممکن است. کاراکتر x و حالت k داده شده است، می‌توان با در نظر گرفتن رشته pat[0..k-1]x که اساسا الحاقی از کاراکترهای الگوی pat[0], pat[1] … pat[k-1]‎ است و کاراکتر x، حالت بعدی را محاسبه کرد.

ایده آن است که طول بلندترین پیش‌وند از الگوی داده شده گرفته شود، به طوری که پیشوند، خود پسوند pat[0..k-1]x است. مقدار طول، حالت بعدی را به دست می‌دهد. برای مثال، در ادامه چگونگی گرفتن حالت بعدی از حالت کنونی ۵ و کاراکتر C‌ در نمودار بالا، بررسی خواهد شد. باید رشته pat[0..4]C را در نظر گرفت که ACACAC است. طول بلندترین پسوند الگو، به طوری که پسوند ACACAC برابر با ۴ است (ACAC). بنابراین، حالت بعدی (از حالت ۵) برابر با ۴ برای کاراکتر C است.

در کدی که در ادامه آمده است، computeTF()‎ اتوماتای متناهی را می‌سازد. پیچیدگی زمانی computeTF()‎ برابر با O(m^3*NO_OF_CHARS)‎ است که در آن، m طول الگو و NO_OF_CHARS اندازه الفبا (تعداد کل کاراکترهای ممکن در الگو و متن) است. پیاده‌سازی، همه پیشوندهای ممکن با شروع از بلندترین حالت ممکن را که می‌تواند پسوند “pat[0..k-1]x” باشد، مورد آزمون قرار می‌دهد. پیاده‌سازی‌های بهتری برای ساخت اتوماتای متناهی در O(m*NO_OF_CHARS)‎ وجود دارد.

پیاده‌سازی الگوریتم اتوماتای متناهی برای جستجوی الگو در سی

// C program for Finite Automata Pattern searching 
// Algorithm 
#include<stdio.h> 
#include<string.h> 
#define NO_OF_CHARS 256 
  
int getNextState(char *pat, int M, int state, int x) 
{ 
    // If the character c is same as next character 
    // in pattern,then simply increment state 
    if (state < M && x == pat[state]) 
        return state+1; 
  
    // ns stores the result which is next state 
    int ns, i; 
  
    // ns finally contains the longest prefix 
    // which is also suffix in "pat[0..state-1]c" 
  
    // Start from the largest possible value 
    // and stop when you find a prefix which 
    // is also suffix 
    for (ns = state; ns > 0; ns--) 
    { 
        if (pat[ns-1] == x) 
        { 
            for (i = 0; i < ns-1; i++) 
                if (pat[i] != pat[state-ns+1+i]) 
                    break; 
            if (i == ns-1) 
                return ns; 
        } 
    } 
  
    return 0; 
} 
  
/* This function builds the TF table which represents4 
    Finite Automata for a given pattern */
void computeTF(char *pat, int M, int TF[][NO_OF_CHARS]) 
{ 
    int state, x; 
    for (state = 0; state <= M; ++state) 
        for (x = 0; x < NO_OF_CHARS; ++x) 
            TF[state][x] = getNextState(pat, M, state, x); 
} 
  
/* Prints all occurrences of pat in txt */
void search(char *pat, char *txt) 
{ 
    int M = strlen(pat); 
    int N = strlen(txt); 
  
    int TF[M+1][NO_OF_CHARS]; 
  
    computeTF(pat, M, TF); 
  
    // Process txt over FA. 
    int i, state=0; 
    for (i = 0; i < N; i++) 
    { 
        state = TF[state][txt[i]]; 
        if (state == M) 
            printf ("\n Pattern found at index %d", 
                                           i-M+1); 
    } 
} 
  
// Driver program to test above function 
int main() 
{ 
    char *txt = "AABAACAADAABAAABAA"; 
    char *pat = "AABA"; 
    search(pat, txt); 
    return 0; 
}

الگوریتم اتوماتای متناهی برای جستجوی الگو در سی‌پلاس‌پلاس

// CPP program for Finite Automata Pattern searching  
// Algorithm  
#include <bits/stdc++.h> 
using namespace std; 
#define NO_OF_CHARS 256  
  
int getNextState(string pat, int M, int state, int x)  
{  
    // If the character c is same as next character  
    // in pattern,then simply increment state  
    if (state < M && x == pat[state])  
        return state+1;  
  
    // ns stores the result which is next state  
    int ns, i;  
  
    // ns finally contains the longest prefix  
    // which is also suffix in "pat[0..state-1]c"  
  
    // Start from the largest possible value  
    // and stop when you find a prefix which  
    // is also suffix  
    for (ns = state; ns > 0; ns--)  
    {  
        if (pat[ns-1] == x)  
        {  
            for (i = 0; i < ns-1; i++)  
                if (pat[i] != pat[state-ns+1+i])  
                    break;  
            if (i == ns-1)  
                return ns;  
        }  
    }  
  
    return 0;  
}  
  
/* This function builds the TF table which represents4  
    Finite Automata for a given pattern */
void computeTF(string pat, int M, int TF[][NO_OF_CHARS])  
{  
    int state, x;  
    for (state = 0; state <= M; ++state)  
        for (x = 0; x < NO_OF_CHARS; ++x)  
            TF[state][x] = getNextState(pat, M, state, x);  
}  
  
/* Prints all occurrences of pat in txt */
void search(string pat, string txt)  
{  
    int M = pat.size();  
    int N = txt.size();  
  
    int TF[M+1][NO_OF_CHARS];  
  
    computeTF(pat, M, TF);  
  
    // Process txt over FA.  
    int i, state=0;  
    for (i = 0; i < N; i++)  
    {  
        state = TF[state][txt[i]];  
        if (state == M)  
            cout<<" Pattern found at index "<< i-M+1<<endl;  
    }  
}  
  
// Driver program to test above function  
int main()  
{  
    string txt = "AABAACAADAABAAABAA";  
    string pat = "AABA";  
    search(pat, txt);  
    return 0;  
}  
  
//This code is contributed by rathbhupendra

الگوریتم اتوماتای متناهی برای جستجوی الگو در جاوا

// Java program for Finite Automata Pattern 
// searching Algorithm 
class GFG { 
      
    static int NO_OF_CHARS = 256; 
    static int getNextState(char[] pat, int M,   
                             int state, int x) 
    { 
          
        // If the character c is same as next 
        // character in pattern,then simply  
        // increment state 
        if(state < M && x == pat[state]) 
            return state + 1; 
              
        // ns stores the result which is next state 
        int ns, i; 
  
        // ns finally contains the longest prefix 
        // which is also suffix in "pat[0..state-1]c" 
  
        // Start from the largest possible value 
        // and stop when you find a prefix which 
        // is also suffix 
        for (ns = state; ns > 0; ns--) 
        { 
            if (pat[ns-1] == x) 
            { 
                for (i = 0; i < ns-1; i++) 
                    if (pat[i] != pat[state-ns+1+i]) 
                        break; 
                    if (i == ns-1) 
                        return ns; 
            } 
        } 
  
            return 0; 
    } 
  
    /* This function builds the TF table which 
    represents Finite Automata for a given pattern */
    static void computeTF(char[] pat, int M, int TF[][]) 
    { 
        int state, x; 
        for (state = 0; state <= M; ++state) 
            for (x = 0; x < NO_OF_CHARS; ++x) 
                TF[state][x] = getNextState(pat, M, state, x); 
    } 
  
    /* Prints all occurrences of pat in txt */
    static void search(char[] pat, char[] txt) 
    { 
        int M = pat.length; 
        int N = txt.length; 
  
        int[][] TF = new int[M+1][NO_OF_CHARS]; 
  
        computeTF(pat, M, TF); 
  
        // Process txt over FA. 
        int i, state = 0; 
        for (i = 0; i < N; i++) 
        { 
            state = TF[state][txt[i]]; 
            if (state == M) 
                System.out.println("Pattern found "
                          + "at index " + (i-M+1)); 
        } 
    } 
  
    // Driver code 
    public static void main(String[] args)  
    { 
        char[] pat = "AABAACAADAABAAABAA".toCharArray(); 
        char[] txt = "AABA".toCharArray(); 
        search(txt,pat); 
    } 
} 
  
// This code is contributed by debjitdbb. 

الگوریتم اتوماتای متناهی برای جستجوی الگو در پایتون

# Python program for Finite Automata  
# Pattern searching Algorithm 
  
NO_OF_CHARS = 256
  
def getNextState(pat, M, state, x): 
    ''' 
    calculate the next state  
    '''
  
    # If the character c is same as next character  
      # in pattern, then simply increment state 
  
    if state < M and x == ord(pat[state]): 
        return state+1
  
    i=0
    # ns stores the result which is next state 
  
    # ns finally contains the longest prefix  
     # which is also suffix in "pat[0..state-1]c" 
  
     # Start from the largest possible value and  
      # stop when you find a prefix which is also suffix 
    for ns in range(state,0,-1): 
        if ord(pat[ns-1]) == x: 
            while(i<ns-1): 
                if pat[i] != pat[state-ns+1+i]: 
                    break
                i+=1
            if i == ns-1: 
                return ns  
    return 0
  
def computeTF(pat, M): 
    ''' 
    This function builds the TF table which  
    represents Finite Automata for a given pattern 
    '''
    global NO_OF_CHARS 
  
    TF = [[0 for i in range(NO_OF_CHARS)]\ 
          for _ in range(M+1)] 
  
    for state in range(M+1): 
        for x in range(NO_OF_CHARS): 
            z = getNextState(pat, M, state, x) 
            TF[state][x] = z 
  
    return TF 
  
def search(pat, txt): 
    ''' 
    Prints all occurrences of pat in txt 
    '''
    global NO_OF_CHARS 
    M = len(pat) 
    N = len(txt) 
    TF = computeTF(pat, M)     
  
    # Process txt over FA. 
    state=0
    for i in range(N): 
        state = TF[state][ord(txt[i])] 
        if state == M: 
            print("Pattern found at index: {}".\ 
                   format(i-M+1)) 
  
# Driver program to test above function             
def main(): 
    txt = "AABAACAADAABAAABAA"
    pat = "AABA"
    search(pat, txt) 
  
if __name__ == '__main__': 
    main() 
  
# This code is contributed by Atul Kumar 

الگوریتم اتوماتای متناهی برای جستجوی الگو در سی‌شارپ

// C# program for Finite Automata Pattern  
// searching Algorithm  
using System; 
  
class GFG 
{ 
  
public static int NO_OF_CHARS = 256; 
public static int getNextState(char[] pat, int M,  
                               int state, int x) 
{ 
  
    // If the character c is same as next  
    // character in pattern,then simply  
    // increment state  
    if (state < M && (char)x == pat[state]) 
    { 
        return state + 1; 
    } 
  
    // ns stores the result  
    // which is next state  
    int ns, i; 
  
    // ns finally contains the longest  
    // prefix which is also suffix in  
    // "pat[0..state-1]c"  
  
    // Start from the largest possible   
    // value and stop when you find a  
    // prefix which is also suffix  
    for (ns = state; ns > 0; ns--) 
    { 
        if (pat[ns - 1] == (char)x) 
        { 
            for (i = 0; i < ns - 1; i++) 
            { 
                if (pat[i] != pat[state - ns + 1 + i]) 
                { 
                    break; 
                } 
            } 
                if (i == ns - 1) 
                { 
                    return ns; 
                } 
        } 
    } 
  
        return 0; 
} 
  
/* This function builds the TF table which  
represents Finite Automata for a given pattern */
public static void computeTF(char[] pat,  
                             int M, int[][] TF) 
{ 
    int state, x; 
    for (state = 0; state <= M; ++state) 
    { 
        for (x = 0; x < NO_OF_CHARS; ++x) 
        { 
            TF[state][x] = getNextState(pat, M,  
                                        state, x); 
        } 
    } 
} 
  
/* Prints all occurrences of  
   pat in txt */
public static void search(char[] pat,  
                          char[] txt) 
{ 
    int M = pat.Length; 
    int N = txt.Length; 
  
  
    int[][] TF = RectangularArrays.ReturnRectangularIntArray(M + 1,  
                                                      NO_OF_CHARS); 
  
    computeTF(pat, M, TF); 
  
    // Process txt over FA.  
    int i, state = 0; 
    for (i = 0; i < N; i++) 
    { 
        state = TF[state][txt[i]]; 
        if (state == M) 
        { 
            Console.WriteLine("Pattern found " +  
                              "at index " + (i - M + 1)); 
        } 
    } 
} 
  
public static class RectangularArrays 
{ 
public static int[][] ReturnRectangularIntArray(int size1,  
                                                int size2) 
{ 
    int[][] newArray = new int[size1][]; 
    for (int array1 = 0; array1 < size1; array1++) 
    { 
        newArray[array1] = new int[size2]; 
    } 
  
    return newArray; 
} 
} 
  
  
// Driver code  
public static void Main(string[] args) 
{ 
    char[] pat = "AABAACAADAABAAABAA".ToCharArray(); 
    char[] txt = "AABA".ToCharArray(); 
    search(txt,pat); 
} 
} 
  
// This code is contributed by Shrikant13

خروجی قطعه کدهای بالا، به صورت زیر است.

  Pattern found at index 0
  Pattern found at index 9
  Pattern found at index 13

منبع [+]

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش برنامه‌نویسی C++‎
• مجموعه آموزش‌های ریاضیات
• یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
• الگوریتم بازی مار و پله همراه با کد — به زبان ساده
• حل مساله n وزیر با الگوریتم پس‌گرد (Backtracking) — به زبان ساده
• الگوریتم جست و جوی دودویی در جاوا اسکریپت — به زبان ساده