فصل هفتم کتاب: بهینه کنترل فعال سازه با رویکرد کلاسیک و هوش مصنوعی
۷-۱- مقدمه
برای حل مسائل بهینه سازی توسط پژوهشگران روشهای گوناگونی پیشنهاد شده است که بعضی از این روشها از ویژگی گرادیان تابع هدف و محدودیت‌های آن برای رسیدن به جواب بهینه استفاده می‌کنند. از آنجایی که در این روشها به اطلاعات گرادیان احتیاج می‌باشد برای توسعه آنها در محاسبه متغییرهای شکل، مشکلات فراوانی ایجاد می‌شود. از آنجایی که حل هر مسئله بهینه سازی در حالت کل بر اساس اصول برنامه ریزی ریاضی استوار می‌باشد استفاده از این متد و روشها بدون آگاهی از اصول روشهای برنامه‌ریزی در واقع غیر ممکن می‌باشد. روشهای برنامه ریزی ریاضی به روشهای جستجوی مستقیم نیز معروف می‌باشند.
۷-۱- مقدمه
برای حل مسائل بهینه سازی توسط پژوهشگران روشهای گوناگونی پیشنهاد شده است که بعضی از این روشها از ویژگی گرادیان تابع هدف و محدودیت‌های آن برای رسیدن به جواب بهینه استفاده می‌کنند. از آنجایی که در این روشها به اطلاعات گرادیان احتیاج می‌باشد برای توسعه آنها در محاسبه متغییرهای شکل، مشکلات فراوانی ایجاد می‌شود. از آنجایی که حل هر مسئله بهینه سازی در حالت کل بر اساس اصول برنامه ریزی ریاضی استوار می‌باشد استفاده از این متد و روشها بدون آگاهی از اصول روشهای برنامه‌ریزی در واقع غیر ممکن می‌باشد. روشهای برنامه ریزی ریاضی به روشهای جستجوی مستقیم نیز معروف می‌باشند.
۷-۲- کلیاتی درباره روشهای بهینه سازی
تاریخ علم بهینه سازی به اوایل قرن نوزدهم باز می‌گردد. تمامی روشهای بهینه سازی قدیمی بر اساس مفهوم مشتق جزیی توابع چند متغیره بیان شده‌اند. چنین روشهایی با عنوان روشهای تحلیلی بهینه سازی شناخته می‌شوند. از آنجا که مفهوم مشتق فقط برای توابع پیوسته تعریف می‌شود، محاسبه بهینه دقیق توابع گسسته با استفاده از روشهای تحلیلی امکان پذیر نیست و اعمال آنها برای توابع گسسته صرفاً تخمینی از مقدار بیهنه و نقطه نظیر آن را به دست می‌آورد.
محاسبات روشهای تحلیلی از یکی از نقاط دامنه تابع آغاز می‌شود و با توجه به گرادیان تابع هدف به صورت خطی به نقطه دیگی منقل می‌شود. محاسبات مذکور برای نقطه جدید تکرار می‌شود تا نقاط بعدی به دست آیند. بدیهی است که عملیات تکراری روشهای تحلیلی تا حصول همگرایی ادامه می‌یابد.
انجام عملیات بهینه سازی بر نقاط خاصی از دامنه تابع هدف و همچنین حرکت خطی میان نقاط مذکور، در بسیاری از موارد باعث همگرایی الگوریتم در بهینه موضعی تابع هدف می‌شود. این ویژگی در شرایطی که تابع هدف دارای نوسانات شدید باشد، تشدید می‌شود. برای جبران این نقیصه، الگوریتم مورد نظر در دفعات مختلف با نقاط آغازین مختلف تکرار می‌شود تا پس از مقایسه نتایج آنها اطمینان کامل از مقادیر محاسبه شده حاصل گردد. مطالعات چند دهه اخیر روشهای عددی مختلفی را برای بهینه سازی توابع مقید ارائه کرده است. این روشها معمولاً با تفکر و استدلالات منطقی در چرخه‌های سعی و خطا گام به گام به سمت نقطه بهینه پیش می‌روند.
در این قسمت سعی بر این است که روشهای عمومی که بیشتر در مسئله‌های بهینه سازی مورد استفاده قرار می‌گیرند، معرفی شوند زیرا بحث درباره همه فنها از ساده تا پیچیده که برای کوتاه کردن زمان تحلیل یا تضمین همگرایی به وجود آمده‌اند، وجود ندارد. اینک به شرح مختصری درباره روشهای مختلف بهینه سازی پرداخته می‌شود.
۷-۳- روشهای برنامه ریزی ریاضی
روشهای برنامه ریزی ریاضی به دو گروه برنامه ریزی خطی و غیر خطی می‌توان تقسیم نمود که در برنامه ریزی خطی، توابع هدف و محدودیت‌های این مسئله بصورت توابع خطی از متغیرهای طراحی می‌باشند و در این روش پاسخ بهینه محلی وجود نداشته و پس از چندین گام تحلیل پاسخ بهینه کلی بطور دقیق به دست می‌آید.
روشهای فوق عملاً در سطح وسیعی از مسائل طراحی سازه‌ها بکار می‌روند. در گروه دوم یعنی مسائل برنامه ریزی غیر خطی بین رفتار سازه و متغیرهای طراحی وابستگی غیر خطی وجود دارد و واضع است که حل این گونه مسائل به سادی امکان پذیر نبوده و یکی از مشکلات آن وجود داشتن چند پاسخ بهینه موضعی می‌باشد.
روشهای برنامه ریزی ریاضی، در حداقل کردن توابعی مرکب از چند متغیر، با توجه به مجموعه‌ای از قیدها مورد استفاده قرار می‌گیرند. برای یافتن حداکثر یا حداقل نا مقید یک توابع چند متغیره می‌توان از روشهای حساب دیفرانسیل استفاده کرد. در این روشها فرض می‌شود که تابع نسبت به متغیرهای طراحی مشتق پذیر بوده و مشتق‌های تابع پیوسته‌اند. برای مسائل که دارای قیدهای مساوی هستند، بیشتر از روش مضاب لاگرانژ استفاده می‌شود اما این روش در حالت کلی به مجموعه‌ای از معادلات غیر خطی می‌انجامد که ممکن است حل آنها مشکل باشد.
روشهای برنامه ریزی غیر خطی، هندسی و درجه دوم یا صحیح را می‌توان برای حل دسته خاصی از مسائلی که با نام روش حل آنها شناخته می‌شوند مورد استفاده قرار داد. همه اینها روشهای عددی هستند، که در آنها از یک جواب اولیه شروع کرده و با روش تکراری جواب نهایی جستجو می‌شود
۷ -۳ -۱- برنامه ریزی خطی
روش برنامه ریزی خطی برای حل مسائلی که در آنها تابع هدف و قیدها توابعی خطی از متغیرهای طراحی هستند بکار می رود. در یک مسئله برنامه ریزی خطی، معادلات محدودیتها ممکن است به صورت نامساوی و یا مساوی باشند. انواع برنامه ریزی خطی مسائل بهینه¬سازی، اولین بار در دهه ۱۹۳۰ توسط اقتصاد دانانی که به مطالعه روشهای تخصصی بهینه سازی منابع می‌پرداختند، شناخته شدند. زمینه کاربرد برنامه ریزی خطی امروزه بقدری زیاد شده است که امکان توصیف همه آنها وجود ندارد.
۷ – ۳ – ۲ – برنامه ریزی غیر خطی
حل مسئله برنامه ریزی غیر خطی به مراتب دشوارتر از برنامه ریزی خطی است. یکی از دشواریهای این برنامه ریزی، وجود پاسخ حداقل محلی یا نسبی است. پاسخ حداقل موضعی، کمترین مقدار را در همسایگی خود برای تابع هدف ایجاد می‌کند با این وجود، این پاسخ نمی‌تواند کمترین مقدار کلی تابع هدف باشد.
۷-۴- روشهای بهینه سازی نامقید
۱٫ با مطالعه مسائل بهینه سازی نامقید، امکان درک مسائل مقید فراهم می‌شود.
۲٫ این نوع مسائل روشهای قدرتمندی را در تحلیل مسائل مهندسی ارائه می‌کنند.
بیشتر تکنیک‌ها و روشهای حل مسائل نامقید، از روندی تکراری برخوردارند. این روشها با استفاده از یک نقطه آغازین {X0} ، که تخمین و برآوردی برای پاسخ مسئله است، کار و محاسبات را شروع کرده و با تکرار دنباله‌ای نقاط، مقدار {XK} بدست می‌آید، به گونه‌ای که با حرکت k به سمت بینهایت، مقدار {XK} به سمت نقطه بهینه و یا دست کم بهینه محلی، همگرا می‌گردد. دنباله {XK} باید در نامعادله 
صدق نماید. واضع است، همگرایی در این روشها بسیار مهم می‌باشد. بیشتر روشها شامل حل دو مسئله پیاپی می‌باشند که در رابطه زیر وجود دارند:
(۱-۷)
در این رابطه {SK} برداری غیر صفر است و جهت‌های این بردار را جهت‌های جستجو می‌نماند. عدد λK طول گام است که می‌تواند مثبت منفی و یا صفر باشد. لذا دو مسئله مورد بحث عبارتند از:
۱٫ انتخاب طول گام
۲٫ انتخاب جهت جستجوی {SK} در نقطه {XK}
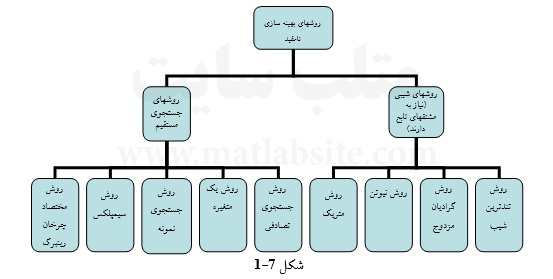
در شکل (۷-۱) روشهای مختلف بهینه سازی نا مقید را می‌توان مشاهده نمود. همانطوری که دیده می‌شود، این روشها در دو زیر مجموعه روشهای شیبی و روشهای جستجوی مستقیم، تقسیم می‌شوند:
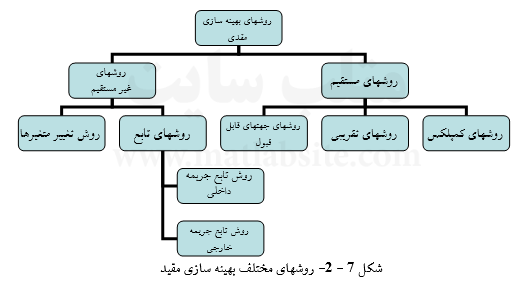
۷ – ۵- روشهای بهینه سازی مقید
در مسئله عملی، متغیرهای طراحی باید معیارهای مختلفی مانند ساخت، کارآیی و … را برقرار سازند که این موارد باعث به وجود آمدن محدودیتهایی در مسئله می‌گردند. به عبارت دیگر هر قید باعث محدود شدن، فضای طراحی شده و از اشتراک نواحی قابل قبول در محدودیتها، ناحیه قابل قبول مسئله بهینه سازی به دست می‌آید.
در این حالت مسئله بهینه سازی مقید به حداقل نمودن تابع حقیقی f بر روی ناحیه قابل قبول از فضای طراحی Rn تبدیل می‌شود، در صورت کلی آن به صورت زیر می‌باشد.
(۲-۷)
ادامه دارد….
آنچه مطالعه کردید، بخش هایی از «فصل هفتم» کتاب «بهینه کنترل فعال سازه با رویکرد کلاسیک و هوش مصنوعی» تالیف «جواد پالیزوان (مدرس دانشگاه) و زند علی روشنی (مدرس دانشگاه)»، می باشد که در راستای معرفی و انتشار رایگان جهت استفاده مخاطبین متلب سایت در اختیار این مجموعه قرار داده شده است.
برای تهیه این کتاب می توانید به این لینک(+) مراجعه نمایید.
همچنین آموزش های زیر در فرادرس نیز مباحثی مرتبط با محتوای این کتاب را پوشش می دهند:
مجموعه: معرفی سایت, مهندسی عمران
Loading...