۸-۱- مقدمه

در این فصل به حل عددی یک ساختمان بلند تحت اثر نیروی زلزله بدون سیستم کنترل و همراه با سیستم‌های کنترل TMD و ATMD پرداخته می‌شود.

 
۸-۱- مقدمه

در این فصل به حل عددی یک ساختمان بلند تحت اثر نیروی زلزله بدون سیستم کنترل و همراه با سیستم‌های کنترل TMD و ATMD پرداخته می‌شود.

در ابتدا ساختمان بلند نمونه را توسط مشخصات برداشت شده از روی نقشه‌های اجرایی آن مدل کرده و سپس ماتریس سختی و جرم آن محاسبه می‌گردد. پس از آن توسط یکی از روش‌های ذکر شده در این فصل ماتریس میرایی سازه محاسبه می‌گردد. بعد از بدست آوردن این مقادیر که پارامترهای اصلی معادله دینامیک حرکت ساختمان بلند است، معادلات دینامیک سازه ساختمان باند تحت اثر نیروی زلزله نوشته شده و در فضای حالت حل می‌گردد. همچنین این معادلات برای ساختمان کنترل شده توسط TMD و ATMD بدست آمده و در فضای حالت حل می‌گردد.

همانطوری که در فصل پنجم در قسمت کنترل فعال اشاره شده است الگوریتم‌های گوناگونی جهت محاسبه نیروی فعال وجود دارد. در اینجا به منظور محاسبه نیروی فعال سیستم ATMD از منطق فازی استفاده شده است. این سیستم بر اساس منطق فازی مقادیر نیروی فعال را در هر زمان با توجه به مقادیر پاسخ سازه (که توسط حس‌گرها دریافت می‌شود)، محاسبه و توسط ضربه زننده به جرم ATMD اعمال می‌کنند.

به منظور مقایسه تاثیر عملکرد کنترل کننده‌های فازی با الگوریتم‌های کلاسیک غیر هوشمند، از الگوریتم کنترل بهینه خطی درجه دو (LQR) استفاده شده است.

کنترل کننده‌ فازی که در این پژوهش مورد تحقیق قرار گرفته است عبارت است از:

• سیستم فازی ممدانی با دو ورودی و یک خروجی همراه با جدول جستجوی فازی ۵×۵;

به جهت مشاهده تاثیر عملکرد هر یک از این سیستم‌های کنترلی بر روی پاسخ‌های ساختمان بلند از ۲ رکورد عدد زلزله با بزرگی، شدت، مدت، و دامنه فرکانسی متفاوت انتخاب شده است.

در نهایت تاثیر این سیستم‌ها بر روی ساختمان بلند نمونه مورد بررسی قرار گرفته است.
فرضیات مساله:

۱٫ رفتار مصالح در محدوده الاستیک خطی فرض شده است.
۲٫ سقف تمام طبقات صلب فرض شده است.
۳٫ تغییر مکان‌ها در محدوده الاستیک خطی و کوچک فرض می‌شوند.

 

۸-۲- ساختمان نمونه

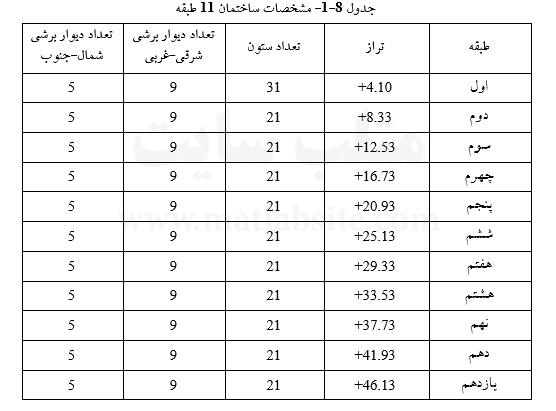
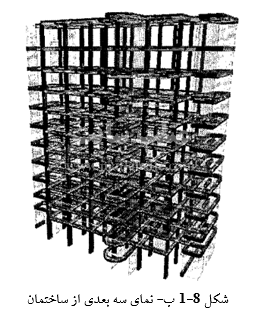
در این کتاب تحقیقات متمرکز بر روی یک ساختمان اداری ۱۱ طبقه شده است، که از نظر سازه‌ای جزء ساختمان‌های بلند متوسط به حساب می‌آید. اسکلت سازه‌ای این ساختمان بتنی می‌باشد.

پلان ساختمان دارای ابعاد ۱۴٫۲۰m×۲۹٫۸۰m می‌باشد جدول (۵-۱) مشخصات اجزاء ساختمان را در طبقات مختلف نشان می‌دهد. کشیدگی ساختمان شمالی-جنوبی می‌باشد. از آنجاییکه مشخصات سازه‌ای ساختمان در جهت شرقی-غربی ضعیف‌تر از این مقادیر در جهت شمالی-جنوبی است، جهت بررسی عملکرد سیستم‌های کنترلی ATMD و TMD نسبت به ساختمان بدون کنترل، مدل سازه را در جهت شرقی غربی در نظر می‌گیریم.

 

۸-۳- مدل اجزاء محدود

آنالیز هر ساختمان بلند متشکل از مجموعه‌ای از اجزاء تیر- شکل و صفحات دیوار برشی را می‌توان با در نظر گرفتن توزیع حقیقی جرم، میرایی و سختی، و پس از آن تعیین فرکانس‌های مودی سازه به صورت متداول انجام داد.

اقدام اول در آنالیز یک ساختمان بلند در برابر بار دینامیکی تعیین ماتریس سختی، جرم و میرایی آن است. از آنجاییکه ماتریس میرایی ماهیتی نامعلوم دارد می‌توان از روش‌های موجود، تقریبی از این ماتریس را توسط ماتریس‌های M(جرم) و K(سختی) بدست آورد. بنابراین پس از بدست آوردن اطلاعات ابعادی و مقاومتی سازه توسط نقشه‌های اجرایی ساختمان مذکور، جهت بدست آوردن پارامترهای دینامیکی سازه نیاز به مدل کردن این سازه در یک نرم افزار اجزاء محدود می‌باشد تا بتوان معادله حرکت دینامیک سازه را پیدا کرد.

طبق فرضیات ارائه شده در مقدمه این فصل سقف کلیه طبقات صلب بوده و رفتار مصالح اجزاء سازه خطی می‌باشد. لذا پارامترهای دینامیکی سازه را می‌توان در فضای خطی و الاستیک بدست آورد. همانطور که در اصول اجزاء محدود سراغ داریم ماتریس سختی یک سازه را می‌توان از روش‌های مختلف بدست آورد. برای این منظور و برای اطمینان از دقت حل مساله سازه توسط دو نرم افزار مدل شده و ماتریس سختی و جرم آن بدست می‌آید. در نهایت ماتریس‌های به دست آمده از دو نرم افزار باهم مقایسه می‌شوند.

در مدل اول سازه در برنامه اجزاء محدودی که برای این منظور نوشته شده است مدل می‌شود. در این برنامه توسط فرمول‌هایی که در اجزاء محدود بدست آمده است مقادیر سختی ستون‌ها و دیوارهای برشی بدست آمده و سپس با سرهم کردن این سختی‌ها سختی کل سازه را بدست آورده می‌شود. و از آنجاییکه سقف‌ها صلب در نظر گرفته شده است، درجات آزادی تبدیل به تغییر مکان افقی طبقات می‌شود. ماتریس کل به ماتریس نهایی فشرده می‌شود. و در نهایت ماتریس جرم نیز به طریق مشابه بدست می‌آید و به صورت توده‌ای به یک ماتریس قطری تبدیل می‌شود.

منطق برنامه نوشته شده به صورت زیر است:

۱٫ خواندن اطلاعات ورودی سازه.

الف) پارامترهای سازه.
ب) مختصات گره‌ها.
پ) اطلاعات اجزاء.
ت) قیود گره‌ها.
ث) تعیین درجات آزادی نهایی جهت ساخت ماتریس سختی و جرم کلی.

۲٫ تولید ماتریس سختی و جرم.

الف) ساخت ماتریس سختی اجزاء.
ب) ماتریس جرم اجزاء.
پ) انتقال به ماتریس سختی و جرم کل سازه.

۳٫ تقلیل ماتریس‌های سختی و جرم.

الف) محاسبه ماتریس سختی تقلیل یافته.
ب) محاسبه ماتریس جرم تقلیل یافته.

پس از وارد نمودن مشخصات به برنامه فوق ماتریس جرم توده‌ای و سختی کل تقلیل یافته بدست می‌آید. حال به منظور مقایسه و اطمینان از صحت حل مساله از روش دیگر که برگرفته از اصول و مفهوم ساخت ماتریس سختی و جرم است، مقادیر ماتریس سختی و میرایی بدست می‌آید. در این روش ماتریس سختی کل تقلیل یافته و ماتریس جرم توده‌ای از محیط اجزاء محدود ETABS بدست می‌آید.

طریقه کار به این شکل است:

گام اول: ابتدا سازه ساختمان بلند را در محیط نرم افزار مدل می‌کنیم.
گام دوم: هیچ نیرویی روی سازه قرار نمی‌دهیم و مقادیر جرم اجزاء سازه را نیز صفر وارد می‌کنیم.

اگر مفهوم ساخت درایه‌های ماتریس سختی را در نظر بگیریم دیده می‌شود که: مقدار درایه K_ij برابر است با نیروی ایجاد شده در درجه آزادی i به ازای تغییر مکان واحد در درجه آزادی j.

گام سوم: از آنجایی که سقف‌ها صلب در نظر گرفته شده است می‌توان یک گره در هر سقف تولید کرد و تمامی درجات آزادی نقاط سقف را به آن نقطه بست. سپس در آن گره تکیه‌گاهی قرار می‌دهیم. حال تغییر مکان واحدی را با توجه به سیستم واحدی که در مدل در نظر گرفته شده – به گره سقف i وارد می‌کنیم و پس از اجرای برنامه میزان نیروی به وجود آمده در تکیه‌گاه هر یک از سقف‌ها را یادداشت می‌کنیم.

گام چهارم: پس از آن تغییر مکان مذکور حذف شده و تغییر مکان واحدی در درجه آزادی بعدی اعمال می‌شود و مقادیر نیروهای اعمالی در تکیه‌گاه هر سقف را دوباره یادداشت می‌کنیم. به همین ترتیب برای تک تک سقف‌های سازه این عمل را انجام می‌دهیم.

گام پنجم: و در نهایت تمام مقادیر بدست آمده را در ماتریس سختی سازه قرار می‌دهیم.

پس از مقایسه ماتریس سختی بدست آمده از برنامه نوشته شده و ماتریس بدست آمده با توجه به مفهوم سختی از محیط ETABS ملاحظه می‌شود که تفاوت کوچکی در درایه‌های دو ماتریس وجود دارد و نتایج تقریباً نتایج مشابهی بدست می‌آید.

در مورد ماتریس جرم با توجه به قابلیت لمپ کردن جرم در سقف که در نرم افزار ETABS وجود دارد، ماتریس جرم lamp بدست می‌آید.

ماتریس رابطه (۸-۱) ماتریس سختی بدست آمده را نشان داده شده است.

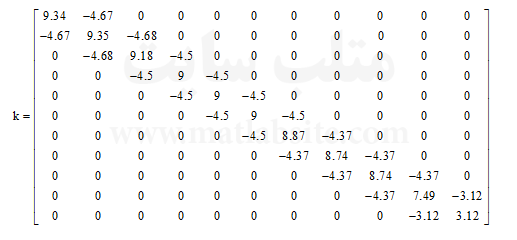
(۱-۸)

مقادیر نوشته شده در ماتریس رابطه (۸-۱) دارای واحد ۱۰۸×۱ N/M می‌باشد.

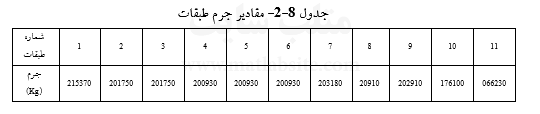
همچنین مقادیر جرم هر طبقه در جدول (۸-۲) آمده است.

 

۸-۴- معادلات دینامیک سازه

۸-۴-۱- تعاریف

تعریف: بار دینامیکی عبارت است از باری که مقدار، جهت و موقعیت آن به شدت با زمان متغیر باشد.

انواع بار دینامیکی: بار دینامیکی از پیش تعیین شده و بار دینامیک تصادفی

بارهای دینامیک از پیش تعیین شده (پریودیک) را می‌توان به دو دسته بارهای هارمونیک و غیر هارمونیک تقسیم کرد. بارهای دینامیک غیر هارمونیک شامل بارهای ضربه‌ای و بارهای عمومی دارای زمان طولانی هستند.

 

۸-۴-۲- معادله حرکت سیستم

هر سیستم دارای یک مدل واقعی می‌باشد که در قدم اول باید تبدیل به یک مدل تحلیلی گردد و در نهایت از مدل تحلیلی، مدل ریاضی مساله بدست می‌آید.

الگوریتم زیر را می‌توان جهت یافتن پاسخ‌های ساختمان بلند در برابر بارهای دینامیکی به کار برد:

گام اول: مدل کردن ساختمان بلند و یافتن درجات آزادی.
گام دوم: یافتن معادلات حرکت ساختمان بلند.
گام سوم: حل معادلات حرکت ساختمان بلند.

سه طریق برای نوشتن معادلات حرکت سازه‌ها وجود دارد:

۱٫ روش تعادل مستقیم با استفاده از قانون دوم نیوتن یا اصل دالامبر.
۲٫ روش اصل کار مجازی یا تغییر مکان مجازی
۳٫ روش واریانس با استفاده از اصل همیلتون .

لازم به ذکر است که در تمام روش‌های فوق در نهایت معادلات حرکت یک سازه به یک شکل در می‌آید. در این جا برای مدل سازی یک ساختمان بلند از اصل دالامبر استفاده می‌شود.

تعریف قانون دوم نیوتن: سرعت تغییرات اندازه حرکت و یا مومنتوم هر ذره مادی بر جرم M برابر است با نیروی وارد بر آن.

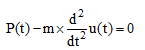
(۲-۸)

طبق قانون فوق اصل دالامبر به صورت زیر نوشته می‌شود.

(۳-۸)

که در آن (u(t تغییر مکان و m جرم ذره است.

اگر سیستم یک درجه آزادی شکل (۵-۲ الف) را در نظر بگیریم، دیاگرام آزاد جسم را تحت اثر نیروها به صورت شکل (۵-۲ ب) در می‌آید.

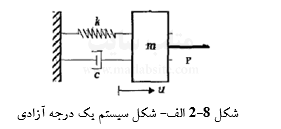
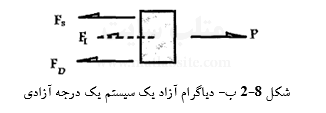
که در شکل (۵-۴):

نیروی خارجی = (P(t) ;
نیروی اینرسی = mu(t) = FI ;
نیروی سختی = Ku(t) = FS ;
نیروی میرایی = Cu(t) = FD ;
که در نهایت پس از جای گذاری، رابطه (۸-۴) بدست می‌آید.

(۴-۸)

با توجه به اینکه ساختمان بلند با فرض صلب بودن سقف‌ها یک سیستم چند درجه آزادی است، معادلات یک سیستم یک درجه آزادی را به سیستم چند درجه آزادی تعمیم می‌دهیم و معادله فوق به صورت معادله دیفرانسیل ماتریسی زیر در می‌آید.

(۵-۸)

که در آن [M] ، [C] و [K] به ترتیب ماتریس جرم، میرایی و سختی سازه است و {u} بردار تغییر مکان ساختمان بلند می‌باشد.

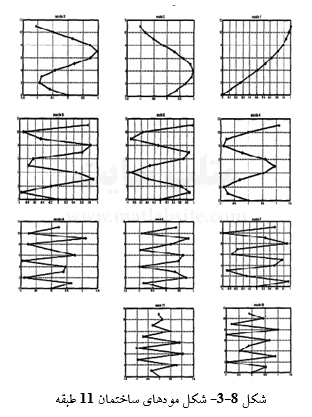
در شکل (۸-۳) شکل مودهای ساختمان یازده طبقه نمونه عددی نشان داده شده است.

 

۸-۴-۳- اثر تحریک تکیه‌گاهی ( نیروی زلزله)

همانطور که می‌دانیم ایجاد تنش‌ها و تغییر مکان‌های دینامیکی نه تنها در اثر اعمال نیروی دینامیکی به جسم ایجاد می‌شود، بلکه ممکن است از حرکت تکیه‌گاهی نیز بوجود آید. یکی از نیروهایی که باعث تحریک تکیه‌گاهی می‌شود نیروی زلزله است.

با نوشتن معادلات یک سیستم یک درجه آزادی تحت اثر تحریک تکیه‌گاهی معادله به صورت زیر در می‌آید.

(۶-۸)

در این رابطه نیروی موثر (mü_g(t)- جایگزین مقدار (P(t شده است، که (ü_g(t شتاب حرکت تکیه‌گاه است.

حال اگر این معادله در مورد یک ساختمان بلند تحت اثر زلزله نوشته شود خواهیم داشت:

(۷-۸)

که در آن [M] ، [C] و [K] به ترتیب ماتریس جرم، میرایی و سختی سازه است و {u} بردار تغییر مکان ساختمان بلند می‌باشد.همچنین {r} برداری با ابعاد (n×۱) که درایه‌های نظیر درجات آزادی در راستای شتاب زلزله مقدار یک و در دیگر درایه‌ها مقدار صفر دارند، و در نهایت (ü_g(t شتاب زلزله را در زمان‌های مختلف نشان می‌دهد.

برای نوشتن معادله حرکت سیستم ساختمان بلند تحت اثر نیروی زلزله پارامترهای دینامیکی [M] ، [C] و [K] و (üg(t نیاز است. ماتریس‌های [M] و [K] که از ساخت مدل اجزاء محدود ساختمان بلند نمونه بدست می‌آید. همچنین شتاب افقی (üg(t نیز از روی شتاب نگاشت‌های زلزله‌های ثبت شده، قابل دست رسی است. اما ماتریس میرایی [C] مقداری نامعلوم دارد، که باید از روابط آن بدست آید.

ادامه دارد….

 

آنچه مطالعه کردید، بخش هایی از «فصل هشتم» کتاب «بهینه کنترل فعال سازه با رویکرد کلاسیک و هوش مصنوعی» تالیف «جواد پالیزوان (مدرس دانشگاه) و زند علی روشنی (مدرس دانشگاه)»، می باشد که در راستای معرفی و انتشار رایگان جهت استفاده مخاطبین متلب سایت در اختیار این مجموعه قرار داده شده است.

برای تهیه این کتاب می توانید به این لینک(+) مراجعه نمایید.

همچنین آموزش های زیر در فرادرس نیز مباحثی مرتبط با محتوای این کتاب را پوشش می دهند:

• فرادرس آموزش کنترل فعال سازه با رویکرد فازی با میراگر (ATMD)
• فرادرس آموزش طراحی فیدبک حالت بهینه برای سیستم های غیر خطی با الگوریتم های تکاملی
• آموزش طراحی کنترل مقاوم H∞/H2 با استفاده از الگوریتم های تکاملی و فراابتکاری