الگوریتم بویر مور برای جستجوی الگو — به زبان ساده
در این مطلب، الگوریتم بویر مور برای جستجوی الگو مورد بررسی قرار گرفته و پیادهسازی آن در زبانهای برنامهنویسی ++C، «جاوا» (Java)، «پایتون» (Python) و #C انجام شده است. این الگوریتم پیکربندیهای گوناگونی دارد که از این جمله میتوان به «الگوریتم بویر مور با هیوریستیک کاراکتر بد» ( Bad character Heuristic) و «الگوریتم بویر مور هیوریستیک پسوند خوب» (Good Suffix Heuristic) اشاره کرد. در این مطلب، هیوریستیک پسوند خوب برای جستجوی الگو مورد بررسی قرار خواهد گرفت. درست مانند هیوریستیک کاراکتر بد، برای هیوریستیک پسوند خوب نیز یک جدول پیشپردازش تولید میشود.
الگوریتم بویر مور هیوریستیک پسوند خوب
فرض میشود که t، زیر رشته متن T است و با زیر رشتهای از الگوی P مطابقت دارد. اکنون، الگو تا هنگامی جا به جا میشود که:
- وقوع دیگری از t در P با t در T مطابقت داشته باشد.
- یک پیشوند از P با پسوند t مطابقت داشته باشد.
- P از t عبور کند.
بررسی موردی ۱: وقوع دیگری از t در P با t در T تطابق دارد.
ممکن است الگوی P حاوی چند وقوع دیگر از T باشد. در چنین شرایطی، تلاش میشود تا الگو برای ترازبندی وقوع با t در T تراز شود. مثال زیر در این راستا قابل توجه است.
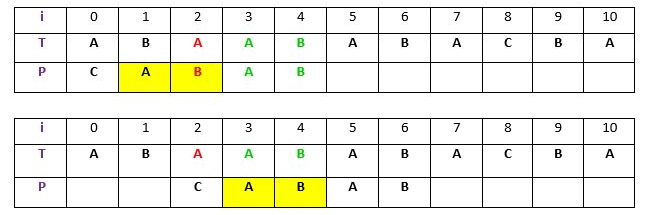

شرح: در مثال بالا، یک زیر رشته از متن T با الگوی P، پیش از عدم تطابق در اندیس ۲، تطابق پیدا کرده است (به رنگ سبز). اکنون، جستجو برای وقوع t (“AB”) در P انجام میشود. یک وقوع در موقعیت ۱ پیدا شده است (در پسزمینه زرد)، بنابران الگو به سمت راست دو بار شیفت داده میشود تا t در P با t در T تطبیق پیدا کند. این یک قانون ضعیف از الگوریتم بویر مور اصلی است و خیلی موثر نیست. در ادامه، قاعده پسوند خوب قوی، مورد بررسی قرار خواهد گرفت.
بررسی موردی ۲: یک پیشوند از P که با پسوند t در R مطابقت دارد.
اینطور نیست که همیشه هم وقوع t در P کشف شود. گاهی اوقات، هیچ وقوعی اصلا وجود ندارد. در چنین شرایطی، گاهی میتوان برای برخی از پسوندهای t که با برخی از پیشوندهای p مطابقت دارند جستجو کرد و تلاش کرد تا آنها را با جا به جایی P تطبیق داد. برای مثال:
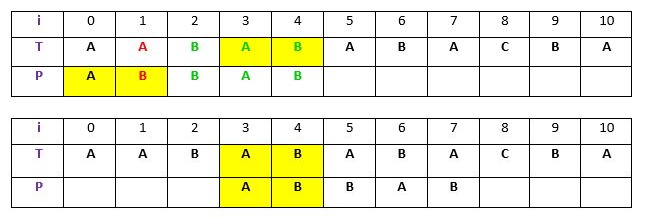
شرح: در مثال بالا، t (“BAB”) با P در اندیس ۴-۲ پیش از عدم تطابق، مطابقت دارد (به رنگ سبز). اما به دلیل اینکه هیچ وقوعی از t در P وجود ندارد، جستجو برای برخی از پیشوندهای P انجام میشود که با برخی از tها مطابقت دارند. پیشوند “AB” (در پسزمینه زرد) که از اندیس ۰ آغاز میشوند و با کل t مطابقت ندارد اما پسوند «AB» با شروع از اندیس ۳ مطابقت دارد. اکنون، الگو سه بار برای تراز کردن پیشوند با پسوند، جا به جا میشود.
بررسی موردی ۳: با عبور p از t
اگر دو حالت بالا ارضا نشدند، الگو جا به جا میشود تا از t عبور کند. برای مثال:
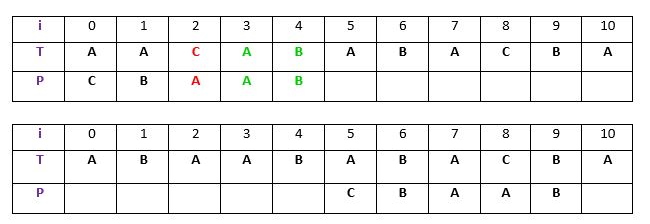
شرح: در مثال بالا، هیچ وقوعی از t (یعنی “AB”) در P وجود ندارد و همچنین، هیچ پیشوندی در P وجود ندارد که با پسوند t مطابقت پیدا کند. بنابراین، در این مورد، هرگز نمیتوان گزینه کاملا منطبقی پیش از اندیس ۴ پیدا کرد، بنابراین، P جا به جا میشود و از t عبور میکند (به اندیس ۵). زیر رشته q = P[i to n] با t در T مطابقت دارد و c = P[i-1] کاراکتر عدم مطابقت است. اکنون، برخلاف حالت ۱، جستجو برای t در P انجام میشود که کاراکتر c مقدم بر آن نیست. سپس، نزدیکترین وقوع با t در T با جا به جایی الگوی P تراز میشود. برای مثال:
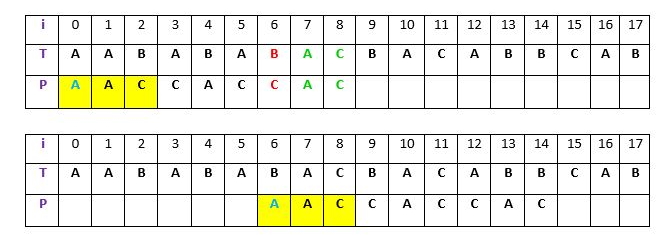
شرح: در مثال بالا، q = P[7 to 8] با t در T مطابقت پیدا میکند. کاراکتر دارای عدم تطابق c در واقع “C” و در موقعیت P[6] است. اکنون، اگر جستجو برای t در P انجام شود، اولین وقوع از t با شروع از موقعیت ۴ انجام میشود. اما در این وقوع، “C” مقدم و برابر با c است؛ بنابراین، از این مورد گذر و جستجو ادامه داده میشود. در موقعیت ۱، وقوع دیگری از t (در پسزمینه زرد) وجود دارد. این وقوع، مقدم “A” را (به رنگ آبی) دارد که برابر با c نیست. بنابراین، الگوی p شش بار شیفت داده میشود تا با وقوع t در T تراز شود. این کار بدین دلیل انجام میشود که در حال حاضر نیز کاراکتر ”c = “C موجب عدم تطابق شده است. بنابراین، هر وقوعی از t با مقدم c در هنگام تراز کردن با t منجر به عدم تطابق میشود؛ به همین دلیل بهتر است از آن گذر شود.
به عنوان بخشی از پیشپردازش، آرایه shift ساخته میشود. هر ورودی [shift[i حاوی الگوی فاصله اگر عدم تطابق در موقعیت i-1 به وقوع بپیوندد، شیفت پیدا خواهد کرد. پسوند الگو در موقعیت i شروع میشود و یک عدم تطابق در i-1 به وقوع میپیوندد. پیشپردازش به طور جداگانهای برای پسوند خوب قوی و حالت دو تشریح شده در بالا انجام میشود.
پیشپردازش برای پسوند خوب قوی
پیش از تشریح پیشپردازش، ابتدا ایده مرز (حاشیه | Border) تشریح میشود. یک مرز، یک زیررشته است که هم پسوند مناسب و هم پیشوند مناسب است. برای مثال، در رشته “ccacc”، یک مرز “c” است، “cc” نیز مرز است زیرا در هر دو انتهای رشته وجود دارد؛ اما “cca” یک مرز نیست.
به عنوان بخشی از پیشپردازش، یک رشته bpos (موقعیت مرز) محاسبه میشود. هر ورودی bpos[i] حاوی اندیس شروع مرز برای پسوندی است که در اندیس i در الگوی داده شده p شروع میشود. پسوند φ در موقعیت m هیچ مرزی ندارد؛ بنابراین bpos[m] برابر با m+1 تنظیم شده است که در آن m طول رشته است. موقعیت جا به جایی به وسیله مرزهایی به دست میآید که نمیتوانند به سمت چپ گسترش پیدا کنند. کد زیر برای پیشپردازش است.
void preprocess_strong_suffix(int *shift, int *bpos,
char *pat, int m)
{
int i = m, j = m+1;
bpos[i] = j;
while(i > 0)
{
while(j <= m && pat[i-1] != pat[j-1])
{
if (shift[j] == 0)
shift[j] = j-i;
j = bpos[j];
}
i--; j--;
bpos[i] = j;
}
}شرح: الگوی ”P = “ABBABAB و m = 7 مفروض است.
- یزرگترین مرز از پسوند “AB” که از موقعیت i = 5 شروع میشود، φ (هیچ چیز) است که در موقعیت ۷ شروع میشود بنابراین bpos[5] = 7.
- در موقعیت i = 2 پسوند “BABAB” است. گستردهترین مرز برای این پسوند برابر با “BAB” است که از موقعیت ۴ شروع میشود، بنابراین j = bpos[2] = 4.
میتوان bpos[i] = j را با استفاده از مثال زیر درک کرد.

اگر کاراکتر # که در موقعیت i-1 است برابر با کاراکتر ? در موقعیت j-1 باشد، میدانیم که مرز، ? + مرز پسوند در موقعیت i خواهد بود که در موقعیت j شروع میشود و برابر با مرز پسوند در موقعیت i-1 است که در j-1 یا bpos[ i-1 ] = j-1 آغاز میشود و یا در کد، به صورت زیر است.
i--;
j--;
bpos[ i ] = jاما اگر کاراکتر # در موقعیت i-1 با کاراکتر ? در موقعیت j-1 مطابقت نداشته باشد، کار جستجو به سمت راست ادامه پیدا میکند. اکنون، اطلاعات زیر به دست میآید:
- پهنای مرز، کوچکتر از مرزی است که در موقعیت j شروع میشود؛ یعنی، کوچکتر از x…φ خواهد بود.
- مرز باید با # شروع شود و با φ پایان پذیرد و یا میتواند خالی باشد (هیچ مرزی وجود ندارد).
با در نظر داشتن دو حقیقت بالا، میتواند به جستجو در زیررشته x…φ از موقعیت j به m ادامه داد. مرز بعدی باید در موقعیت j = bpos[j] باشد. پس از به روز رسانی j، مجددا کاراکترها در موقعیت j-1 (?) با # مقایسه میشوند و اگر برابر باشند، مرز به دست آمده، در غیر این صورت، جستجو به راست تا هنگامی که j>m باشد، ادامه پیدا میکند. این فرایند در کد زیر نمایش داده شده است.
while(j <= m && pat[i-1] != pat[j-1])
{
j = bpos[j];
}
i--; j--;
bpos[i]=j;در کد بالا، شرط زیر قابل توجه است.
pat[i-1] != pat[j-1]این شرایطی است که در حالت دو مورد برسی قرار گرفت. هنگامی که کاراکتر پیش از وقوع t در P متفاوت از کاراکتر دارای عدم تطابق در P باشد، از چشمپوشی از وقوع جلوگیری و الگوی شیفت داده میشود. بنابراین، در اینجا P[i] == P[j] اما P[i-1] != p[j-1] ، بنابراین، الگو از i به j شیفت داده میشود. بنابراین، shift[j] = j-i ثبت کننده برای j است. بنابراین، هنگامی که هرگونه عدم تطابقی در موقعیت j به وقوع بپیوندد، موقعیتهای الگوی shift[j+1] به راست شیفت داده میشود. در کد بالا، شرط زیر بسیار مهم است.
if (shift[j] == 0 )شرطی که در بالا بیان شده، از ویرایش مقدار shift[j] از پسوندی که مرز مشابهی دارد جلوگیری میکند. برای مثال، الگوی P = “addbddcdd” هنگامی قابل در نظر گرفتن است که ما bpos[ i-1 ] را برای i = 4 و سپس، j = 7 محاسبه میکنیم. در این شرایط، مقدار shift[ 7 ] = 3 به تدریج تنظیم میشود. اکنون، اگر bpos[ i-1 ] برای i = 1 محاسبه شود، j = 7 خواهد بود و مقدار shift[ 7 ] = 6 تنظیم خواهد شد اگر هیچ تست shift[ j ] == 0 وجود نداشته باشد. این یعنی اگر یک عدم تطابق در موقعیت ۶ وجود داشته باشد، الگوی P سه موقعیت به سمت راست شیفت داده میشود، نه شش موقعیت.
پیشپردازش برای بررسی موردی ۲:
در پیشپردازش برای بررسی موردی ۲، برای هر پسوند گستردهترین مرز از کل الگو، گه در آن پسوند وجود دارد، تعیین میشود. نقطه شروع از گستردهترین مرز از الگو در bpos[0] ذخیره میشود. در الگوریتم پیشپردازشی که در ادامه میآید، مقدار bpos[0] در ابتدا در همه ورودیهای آزاد شیفت آرایه مورد استفاده قرار میگیرد. اما هنگامی که پسوند الگو کوتاهتر از bpos[0] خواهد شد، الگوریتم با مرز گستردهتر بعدی از الگو ادامه پیدا میکند، یعنی bpos[j]. پیادهسازی آنچه بیان شد در ادامه آمده است.
پیادهسازی در ++C
/* C program for Boyer Moore Algorithm with
Good Suffix heuristic to find pattern in
given text string */
#include <stdio.h>
#include <string.h>
// preprocessing for strong good suffix rule
void preprocess_strong_suffix(int *shift, int *bpos,
char *pat, int m)
{
// m is the length of pattern
int i=m, j=m+1;
bpos[i]=j;
while(i>0)
{
/*if character at position i-1 is not equivalent to
character at j-1, then continue searching to right
of the pattern for border */
while(j<=m && pat[i-1] != pat[j-1])
{
/* the character preceding the occurrence of t in
pattern P is different than the mismatching character in P,
we stop skipping the occurrences and shift the pattern
from i to j */
if (shift[j]==0)
shift[j] = j-i;
//Update the position of next border
j = bpos[j];
}
/* p[i-1] matched with p[j-1], border is found.
store the beginning position of border */
i--;j--;
bpos[i] = j;
}
}
//Preprocessing for case 2
void preprocess_case2(int *shift, int *bpos,
char *pat, int m)
{
int i, j;
j = bpos[0];
for(i=0; i<=m; i++)
{
/* set the border position of the first character of the pattern
to all indices in array shift having shift[i] = 0 */
if(shift[i]==0)
shift[i] = j;
/* suffix becomes shorter than bpos[0], use the position of
next widest border as value of j */
if (i==j)
j = bpos[j];
}
}
/*Search for a pattern in given text using
Boyer Moore algorithm with Good suffix rule */
void search(char *text, char *pat)
{
// s is shift of the pattern with respect to text
int s=0, j;
int m = strlen(pat);
int n = strlen(text);
int bpos[m+1], shift[m+1];
//initialize all occurrence of shift to 0
for(int i=0;i<m+1;i++) shift[i]=0;
//do preprocessing
preprocess_strong_suffix(shift, bpos, pat, m);
preprocess_case2(shift, bpos, pat, m);
while(s <= n-m)
{
j = m-1;
/* Keep reducing index j of pattern while characters of
pattern and text are matching at this shift s*/
while(j >= 0 && pat[j] == text[s+j])
j--;
/* If the pattern is present at the current shift, then index j
will become -1 after the above loop */
if (j<0)
{
printf("pattern occurs at shift = %d\n", s);
s += shift[0];
}
else
/*pat[i] != pat[s+j] so shift the pattern
shift[j+1] times */
s += shift[j+1];
}
}
//Driver
int main()
{
char text[] = "ABAAAABAACD";
char pat[] = "ABA";
search(text, pat);
return 0;
}پیادهسازی در جاوا
/* Java program for Boyer Moore Algorithm with
Good Suffix heuristic to find pattern in
given text string */
class GFG
{
// preprocessing for strong good suffix rule
static void preprocess_strong_suffix(int []shift, int []bpos,
char []pat, int m)
{
// m is the length of pattern
int i = m, j = m + 1;
bpos[i] = j;
while(i > 0)
{
/*if character at position i-1 is not
equivalent to character at j-1, then
continue searching to right of the
pattern for border */
while(j <= m && pat[i - 1] != pat[j - 1])
{
/* the character preceding the occurrence of t
in pattern P is different than the mismatching
character in P, we stop skipping the occurrences
and shift the pattern from i to j */
if (shift[j] == 0)
shift[j] = j - i;
//Update the position of next border
j = bpos[j];
}
/* p[i-1] matched with p[j-1], border is found.
store the beginning position of border */
i--; j--;
bpos[i] = j;
}
}
//Preprocessing for case 2
static void preprocess_case2(int []shift, int []bpos,
char []pat, int m)
{
int i, j;
j = bpos[0];
for(i = 0; i <= m; i++)
{
/* set the border position of the first character
of the pattern to all indices in array shift
having shift[i] = 0 */
if(shift[i] == 0)
shift[i] = j;
/* suffix becomes shorter than bpos[0],
use the position of next widest border
as value of j */
if (i == j)
j = bpos[j];
}
}
/*Search for a pattern in given text using
Boyer Moore algorithm with Good suffix rule */
static void search(char []text, char []pat)
{
// s is shift of the pattern
// with respect to text
int s = 0, j;
int m = pat.length;
int n = text.length;
int []bpos = new int[m + 1];
int []shift = new int[m + 1];
//initialize all occurrence of shift to 0
for(int i = 0; i < m + 1; i++)
shift[i] = 0;
//do preprocessing
preprocess_strong_suffix(shift, bpos, pat, m);
preprocess_case2(shift, bpos, pat, m);
while(s <= n - m)
{
j = m - 1;
/* Keep reducing index j of pattern while
characters of pattern and text are matching
at this shift s*/
while(j >= 0 && pat[j] == text[s+j])
j--;
/* If the pattern is present at the current shift,
then index j will become -1 after the above loop */
if (j < 0)
{
System.out.printf("pattern occurs at shift = %d\n", s);
s += shift[0];
}
else
/*pat[i] != pat[s+j] so shift the pattern
shift[j+1] times */
s += shift[j + 1];
}
}
// Driver Code
public static void main(String[] args)
{
char []text = "ABAAAABAACD".toCharArray();
char []pat = "ABA".toCharArray();
search(text, pat);
}
}
// This code is contributed by 29AjayKumarپیادهسازی در پایتون ۳
# Python3 program for Boyer Moore Algorithm with
# Good Suffix heuristic to find pattern in
# given text string
# preprocessing for strong good suffix rule
def preprocess_strong_suffix(shift, bpos, pat, m):
# m is the length of pattern
i = m
j = m + 1
bpos[i] = j
while i > 0:
'''if character at position i-1 is
not equivalent to character at j-1,
then continue searching to right
of the pattern for border '''
while j <= m and pat[i - 1] != pat[j - 1]:
''' the character preceding the occurrence
of t in pattern P is different than the
mismatching character in P, we stop skipping
the occurrences and shift the pattern
from i to j '''
if shift[j] == 0:
shift[j] = j - i
# Update the position of next border
j = bpos[j]
''' p[i-1] matched with p[j-1], border is found.
store the beginning position of border '''
i -= 1
j -= 1
bpos[i] = j
# Preprocessing for case 2
def preprocess_case2(shift, bpos, pat, m):
j = bpos[0]
for i in range(m + 1):
''' set the border position of the first character
of the pattern to all indices in array shift
having shift[i] = 0 '''
if shift[i] == 0:
shift[i] = j
''' suffix becomes shorter than bpos[0],
use the position of next widest border
as value of j '''
if i == j:
j = bpos[j]
'''Search for a pattern in given text using
Boyer Moore algorithm with Good suffix rule '''
def search(text, pat):
# s is shift of the pattern with respect to text
s = 0
m = len(pat)
n = len(text)
bpos = [0] * (m + 1)
# initialize all occurrence of shift to 0
shift = [0] * (m + 1)
# do preprocessing
preprocess_strong_suffix(shift, bpos, pat, m)
preprocess_case2(shift, bpos, pat, m)
while s <= n - m:
j = m - 1
''' Keep reducing index j of pattern while characters of
pattern and text are matching at this shift s'''
while j >= 0 and pat[j] == text[s + j]:
j -= 1
''' If the pattern is present at the current shift,
then index j will become -1 after the above loop '''
if j < 0:
print("pattern occurs at shift = %d" % s)
s += shift[0]
else:
'''pat[i] != pat[s+j] so shift the pattern
shift[j+1] times '''
s += shift[j + 1]
# Driver Code
if __name__ == "__main__":
text = "ABAAAABAACD"
pat = "ABA"
search(text, pat)
# This code is contributed by
# sanjeev2552پیادهسازی در #C
/* C# program for Boyer Moore Algorithm with
Good Suffix heuristic to find pattern in
given text string */
using System;
class GFG
{
// preprocessing for strong good suffix rule
static void preprocess_strong_suffix(int []shift,
int []bpos,
char []pat, int m)
{
// m is the length of pattern
int i = m, j = m + 1;
bpos[i] = j;
while(i > 0)
{
/*if character at position i-1 is not
equivalent to character at j-1, then
continue searching to right of the
pattern for border */
while(j <= m && pat[i - 1] != pat[j - 1])
{
/* the character preceding the occurrence of t
in pattern P is different than the mismatching
character in P, we stop skipping the occurrences
and shift the pattern from i to j */
if (shift[j] == 0)
shift[j] = j - i;
//Update the position of next border
j = bpos[j];
}
/* p[i-1] matched with p[j-1], border is found.
store the beginning position of border */
i--; j--;
bpos[i] = j;
}
}
//Preprocessing for case 2
static void preprocess_case2(int []shift, int []bpos,
char []pat, int m)
{
int i, j;
j = bpos[0];
for(i = 0; i <= m; i++)
{
/* set the border position of the first character
of the pattern to all indices in array shift
having shift[i] = 0 */
if(shift[i] == 0)
shift[i] = j;
/* suffix becomes shorter than bpos[0],
use the position of next widest border
as value of j */
if (i == j)
j = bpos[j];
}
}
/*Search for a pattern in given text using
Boyer Moore algorithm with Good suffix rule */
static void search(char []text, char []pat)
{
// s is shift of the pattern
// with respect to text
int s = 0, j;
int m = pat.Length;
int n = text.Length;
int []bpos = new int[m + 1];
int []shift = new int[m + 1];
// initialize all occurrence of shift to 0
for(int i = 0; i < m + 1; i++)
shift[i] = 0;
// do preprocessing
preprocess_strong_suffix(shift, bpos, pat, m);
preprocess_case2(shift, bpos, pat, m);
while(s <= n - m)
{
j = m - 1;
/* Keep reducing index j of pattern while
characters of pattern and text are matching
at this shift s*/
while(j >= 0 && pat[j] == text[s + j])
j--;
/* If the pattern is present at the current shift,
then index j will become -1 after the above loop */
if (j < 0)
{
Console.Write("pattern occurs at shift = {0}\n", s);
s += shift[0];
}
else
/*pat[i] != pat[s+j] so shift the pattern
shift[j+1] times */
s += shift[j + 1];
}
}
// Driver Code
public static void Main(String[] args)
{
char []text = "ABAAAABAACD".ToCharArray();
char []pat = "ABA".ToCharArray();
search(text, pat);
}
}
// This code is contributed by PrinciRaj1992
خروجی قطعه کدهای بالا، به صورت زیر است.
pattern occurs at shift = 0
pattern occurs at shift = 5اگر نوشته بالا برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای برنامه نویسی
- آموزش ساختمان دادهها
- مجموعه آموزشهای ساختمان داده و طراحی الگوریتم
- رنگآمیزی گراف به روش حریصانه — به زبان ساده
- الگوریتم دایجسترا (Dijkstra) — از صفر تا صد
- الگوریتم پریم — به زبان ساده
- متن کاوی (Text Mining) — به زبان ساده
منبع [+]
مجموعه: بازشناسی الگو, برنامه نویسی, مهندسی کامپیوتر برچسب ها: Boyer Moore, Boyer Moore Algorithm, Good Suffix heuristic, الگوریتم بویر مور, جستجوی الگو, هیوریستیک پسوند خوب




 (No Ratings Yet)
(No Ratings Yet)