۶-۱- مقدمه

(همه چیز بطور نسبی درست یا غلط است).
جمله فوق در واقع در میان متفکران نظریه فازی به عنوان یک اصل در مقابل اصل «طرد شق ثالث» متفکران نظریه دو ارزشی تلقی می‌شود. جملاتی مثل «اول فروردین ۱۳۸۱ روز شنبه»،«بقراط مرده است»،«سقراط فانی است»، درجه حرارت هوا °۳۰ است. ۲+۲=۴ تنها عدد اول زوج ۲ است. «۳ عدد اول نیست.» و از این قبیل یا صادق هستند و یا نیستند و از این دو حال خارج نمی‌شوند. از ابتدای حیات ریاضیات صادق یا کاذب بودن گزاره‌ها مسلم و قطعی فرض می‌شد و شرایطی خارج از این دو حالت قابل تصور نبود. اساس علم منطق و ریاضی سیستم دو ارزشی بوده و به تبع آن جهان علم بر این مبنا پایه‌ریزی گردیده است. بارت کاسکو در کتاب تفکر فازی چنین نگرشی را نگرش سیاه و سفید می‌نامد و ان را یک اشتباه بزرگ علم قلمداد می‌کند و مدعی است که علم واقعیت های خاکستری یا فازی را با ابزار سیاه و سفید به نمایش گذاشته است و بدین گونه به نظر می‌رسد که واقعیت‌ها نیز تنها سیاه یا سفید هستند [Wang, et al. 1982].

 

۶-۱- مقدمه

(همه چیز بطور نسبی درست یا غلط است).
جمله فوق در واقع در میان متفکران نظریه فازی به عنوان یک اصل در مقابل اصل «طرد شق ثالث» متفکران نظریه دو ارزشی تلقی می‌شود. جملاتی مثل «اول فروردین ۱۳۸۱ روز شنبه»،«بقراط مرده است»،«سقراط فانی است»، درجه حرارت هوا °۳۰ است. ۲+۲=۴ تنها عدد اول زوج ۲ است. «۳ عدد اول نیست.» و از این قبیل یا صادق هستند و یا نیستند و از این دو حال خارج نمی‌شوند. از ابتدای حیات ریاضیات صادق یا کاذب بودن گزاره‌ها مسلم و قطعی فرض می‌شد و شرایطی خارج از این دو حالت قابل تصور نبود. اساس علم منطق و ریاضی سیستم دو ارزشی بوده و به تبع آن جهان علم بر این مبنا پایه‌ریزی گردیده است. بارت کاسکو در کتاب تفکر فازی چنین نگرشی را نگرش سیاه و سفید می‌نامد و ان را یک اشتباه بزرگ علم قلمداد می‌کند و مدعی است که علم واقعیت های خاکستری یا فازی را با ابزار سیاه و سفید به نمایش گذاشته است و بدین گونه به نظر می‌رسد که واقعیت‌ها نیز تنها سیاه یا سفید هستند [Wang, et al. 1982].

آنچه محل تامل نظریه‌پردازان فازی می‌باشد عبارت‌هایی است که در آنها مباحثی وجود دارد که چندان شفاف و واضح نیستند و رگه‌هایی از ابهام (vagueness) و عدم قطعیت (Uncertainty) در آنها وجود دارد. اگر در یک جمع از حضار بخواهیم افراد متاهل دست خود را بالا ببرند یک مجموعه مشخص متاهل و یک مجموعه مشخص غیر متاهل خواهیم داشت یا اگر بخواهیم می‌توانیم به راحتی مجموعه زنان و مردان را تفکیک کنیم، اما در همان جمع اگر بخواهیم افرادی که از شغل خود رضایت دارند دست خود را بالا ببرند در کنار کسانی که بطور واضح دست خود را بالا برده‌اند و کسانی که با خیال راحت دستهایشان پایین است افرادی را خواهیم دید که در بالا نگه داشتن دستهای خود دچار تردید هستند و دستشان کم و بیش بالاست و یا کمی بالا رفته است که چنین واکنشی شاید نشان دهنده رضایت نسبی و یا کم رضایتی شغلی باشد. مباحثی مثل فانی و غیر فانی، زنده و مرده، مرد و زن، سفید و سفید و از این قبیل مجموعه هایی مشخص، قطعی و دقیق (Precise) هستند که اعضای کاملاً مشخص دارند که تردیدی در تعلق شی خاصی مثل a در آنها وجود ندارد. اما مجموعه انسانهای خوشحال، راضی، بلند قد، زیبا، باهوش، فعال و لایق دارای یک سری ویژگیهای کیفی هستند که برای انها مرز مشخص و قطعی و مسلمی وجود ندارد. این مفاهیم زبانی دارای ابهام هستند. در کتب منابع مختلف ربان‌شناسی، دستور زبان و فلسفه و منطق تعاریف و تقسیم‌بندی‌های متفاوتی از مقوله ابهام (در برخی موارد به Ambiguity اشاره شده است) آمده است.

بشر در زندگی روزمره خود با این نوع عبارت‌ها بسیار سر و کار دارد و در استدلالهای خود از آنها استفاده می‌کند و چه بسا که درصد بالایی از استدلالها را چنین تشکیل می‌دهند. عبارتهایی مثل «امروز هوا گرم است»، «هوا ابریست»، «من گرسنه هستم»، «این رنگ روشن است»، «فردا زود می‌آیم» و از این قبیل مباحثی هستند که حالتهایی کیفی را بیان می‌کنند و این حالتهای کیفی در شرایط و موقعیت‌های متفاوت عملکردی متفاوت دارند. مثلا عبارت «امروز هوا گرم است» اگر در یکی از روزهای دی ماه گفته شود نسبت به زمانی که در مرداد ماه بیان شود بر شرایط کمی بسیار متفاوتی دلالت دارد. شنونده این جمله که در آن شرایط قرار دارد بدون هیچ توضیح اضافه‌ای می‌تواند درک درستی نسبت به این جمله داشته باشد اما اگر گیرنده این جمله یک سیستم کامپیوتری با سیستم ارزش‌گذاری ۰ و ۱ باشد و هیچ اطلاعات دیگری نیز به او جز درجه حرارت هوا ندهیم، در مرداد به این جمله ارزش یک و در دی ارزش صفر می‌دهد اما یک سیستم هوشمند فازی در مرداد به این عبارت ارزش یک و در روز زمستانی ارزش ۳/۰ (به عنوان مثال) خواهد داد. چرا که در سیستم دو ارزشی (سیستم کامپیوترهای رقمی) یک مرز مشخص و قطعی، مثلاً °۲۰ باید مشخص شود و اگر حتی به اندازه صدم درجه سانتیگراد تفاوت نسبت به این مرز مشخص وجود داشته باشد ارزش جمله مورد نظر تغییر خواهد یافت. مثلاً حتی °۹۹/۱۹ ، «هوا گرم است.» ارزش صفر دارد و °۲۰، «هوا گرم است.» ارزش یک را خواهد داشت. بنابر آنچه گفته شد حال می‌توان درکی نسبی از مفهوم کلمه فازی داشت. کلمه‌ای که اولین بار دکتر لطفی‌زاده آن را وارد جهان علم نمود.

واژه فازی در فرهنگ آکسفورد (Oxford) با معانی مبهم، گنگ، نادقیق، گیج، مغشوش، در هم و نامشخص آمده است [Wang, et al. 1982] معانی دیگری مثل کرکی، در هم و بر هم، پرزدار، تیره و نامعلوم نیز از جمله معانی دیگر ذکر شده برای واژه فازی می‌باشد ]آذر، ۱۳۸۰[. در مجموع واژه فازی به مفهومی بدون مرز دقیق اشاره دارد [Morgan, et al. 1998] دکتر لطفی‌زاده در پاسخ به این سوال که چرا کلمه فازی را برای این نظریه انتخاب کرده است می‌گوید [Morgab, et al. 1998]:

«من کلمه فازی را انتخاب کردم چون احساس می‌کردم که این کلمه با بیشترین دقت آنچه را در این نظریه آمده است، توصیف می‌کند. من می‌توانستم کلمه محترمانه‌تری را که کمتر عوامانه باشد انتخاب کنم. پس در مورد کلمه های نرم (Soft)، غیر دقیق (Un sharp)، کدر و در هم و بر هم (Blurred) و یا قابل ارتجاع و انعطاف (Elastic) فکر کردم اما هیچ کدام اینها آنچه را که در ذهن من بود به دقت توصیف نمی‌کردند پس در نهایت فازی را در این جایگاه قرار دادم.»

در زبان فارسی در برخی منابع برای کلمه فازی معادل‌هایی مانند نادقیق آورده شده است. اما آنچه که بیشتر شایع و رایج گردیده است همان لفظ فازی می‌باشد.

همانطور که گفته شد با داشتن چنین نگرشی به این نوع از مقوله‌های زبانی نظریه مجموعه‌های فازی یعنی مجموعه‌هایی که عضویت اعضاء متعلق به آنها نسبت به مجموعه‌های کلاسیک متفاوت بود، شکل گرفت و در مقاله‌ای در سال ۱۹۶۵ بوسیله دکتر زاده مطرح شد و از آن پس در شاخه‌های مختلف علمی مورد استفاده قرار گرفت که یکی از این شاخه‌ها علم منطق است.

مطابق با فرهنگ وبستر (Webster) منطق، علم اصول استدلال صوری تجویزی (Science of the normative formal of reasoning) می‌باشد. به این معنی، منطق فازی به بررسی اصول استدلال تقریبی (Approximate Reasoning) صوری می‌پردازد که به استدلال دقیق (Precise Reasoning) به عنوان یک مورد مرزی می‌نگرد [Zadeh, 1988].

بنابراین منطق فازی با به کارگیری ایده نظریه مجموعه‌های فازی و کنار گذاردن ایده دو ارزشی شکل گرفت و استدلالهایی را که سالها به جهت خوش تعریف نبودن قیود و مقوله های از حوزه استدلالات صوری کنار گذارده شده بودند مورد مطالعه و بررسی قرار داد. در ادامه تاریخچه مختصری از شکل‌گیری و پیشرفت نظریه فازی ارائه خواهد شد.

 

۶-۲- مجموعه‌های فازی

۶-۲-۱- تعاریف و مفاهیم مجموعه‌های فازی

یک روش مفید در تعریف و نشان دادن یک مجموعه استفاده از مفهوم تابع مشخصه (Characteristic Function) است.

فرض کنید A یک زیر مجموعه از مجموعه مرجع X باشد. تابع مشخصه A به صورت زیر تعریف و نشان داده می‌شود [طاهری، ۱۳۷۸].

(۱-۶)

ملاحظه می‌کنید که دامنه تابع نشان‌گر مجموعه مرجع، و برد آن مجموعه دو عضوی {۱و۰}است.

مثال

در مجموعه زیر تابع مشخصه به این صورت تعریف می‌شود.

{A={1,2,3
Chf_A(1)=1
Chf_A(2)=1
Chf_A(5)=0

در واقع در مجموعه‌های معمولی تابع مشخصه (chf) درجه عضویت را در مجموعه نشان می‌دهد.

حال جرقه مجموعه‌های فازی اینجا زده می‌شود یعنی اینکه هیچ الزامی وجود ندارد که تابع chf دارای برد {۰,۱} باشد به طور مثال ما از مجموعه مرجع X که مجموعه تمام سیبها است، می‌خواهیم به A (مجموعه سیب‌های کاملاً سرخ) دسترسی پیدا کنیم. سیب اولی را که انتخاب می‌کنیم کاملاً زرد بوده و در واقع chf آن صفر است. سیب دوم کاملاً سرخ بوده و عضو مجموعه سرخ با chf یک می‌باشد. ولی یک سیب دارای رنگ سرخ با لکه‌های زرد است. این سیب را نه می‌توان در مجموعه A قرار داد و نه می‌توان در مجموعه A قرار نداد. ولی با کمی تغییر در تعاریف می‌توان این کار را به راحتی انجام داد. یعنی این سیب تا حدودی عضو این مجموعه سیب‌های سرخ است (مثلاً ۷۰٪). پس اگر برد تابع chf از {۰,۱} به [۰,۱] تغییر کند. این سیب با chfx(a)=0.7 عضو این مجموعه است. از این به بعد این مجموعه را که این گونه تعریف کردیم مجموعه فازی و تابع مشخصه آن را تابع عضویت (MF) Membership Function می‌نامیم چون در واقع این تابع درجه تعلق عضو را به مجموعه فازی A نشان می‌دهد و با μA(x) نشان می‌دهیم.

فرض کنید [X=[0,2000 باشد. یک زیرمجموعه فازی از X که نشان دهنده ویژگی «نزدیک ۱۰۰۰» باشد را می‌توان توسط تابع عضویت زیر تعریف کرد.

(۲-۶)

 

۶-۲-۲- چند مفهوم مقدماتی

به فرض اینکه X یک مجموعه مرجع و A یک زیرمجموعه فازی آن باشد [طاهری، ۱۳۷۸].

الف) تکیه گاه (Supp A) A : مجموعه نقاطی در X که μA(x)>0 باشد را گویند (نقاطی که تا حدودی عضو مجموعه ما هستد).

ب) ارتفاع (SUPx μA(x)) A : یعنی بیشترین μA(x) که یک عضو در مجموعه A دارد را گویند (تابع عضویت نقطه‌ای که بیشترین عضویت را نسبت به مجموعه دارد.)

ت) مجموعه نرمال: مجموعه‌ای که ارتفاع آن برابر یک باشد. یعنی μA(x) ≤۱ باشد (مجموعه‌ای که حداقل یک عضو با صد در صد عضویت در آن وجود داشته باشد)

ث) نقطه گذر (معبر A): نقطه‌ای از مجموعه با μA(x)=0.5 را گویند.

 

۶-۲-۳- نماد گذاری

نشانگذاری در مجموعه‌های فازی روش‌های مختلفی دارد، که به ذکر آن می‌پردازیم [زاهدی، ۱۳۷۸].

روش الف) کاربرد مستقیم تابع عضویت.

به طور مثال:

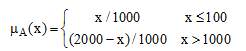
(۳-۶)

روش ب) به صورت زوج مرتب

A={(x,μA(x)); xєX}

(۴-۶)

روش پ) برای مجموعه‌های متناهی و نامتناهی قابل شمارش.

(۵-۶)

• علامت فوق علامت جمع نبوده و صرفا برای نشان دادن مجموعه است.

روش ت) برای مجموعه ناشمارا.

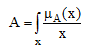
(۶-۶)

• علامت فوق، علامت انتگرال نبوده و صرقاً برای نشان دادن مجموعه است.

 

۴-۲-۴- عملگرهای مجموعه‌ای

الف) دو مجموعه B، A معادلند (equal) اگر و تنها اگر برای هر 

ب) A زیرمجموعه B است اگر و تنها اگر برای تمامی مقادیر 

ت) مکمل مجموعه فازی (Compliment)A به این شکل تعریف می‌شود

ث) برای هر 

• norm عملگری است که باید شرایط مکمل را دارا باشد که در ادامه توضیحات کامل در خصوص آن داده می‌شود.

ج) اجتماع (Union) A,B یک مجموعه فازی است در X که با نمایش می‌دهند و تابع عضویت آن به صورت زیر است.

(۷-۶)

• S-norm عملگری است که باید شرایط اجتماع را دارا باشد که در ادامه توضیحات کامل در خصوص آن داده می‌شود.

ث) اشتراک (Intersection) A,B یک مجموعه فازی است در X که با نمایش می‌دهند و تابع عضویت ان به صورت زیر است.

(۸-۶)

• T-norm عملگر است که باید شرایط اشتراک را دارا باشد که در ادامه توضیحات کامل آن داده می‌شود.

عملگرهای C,T,S همگی به طور مفروض عملگری‌اند که برای اقناع خواص خود باید شرایطی را ارضاء کنند، که به تفصیل به آنها می‌پردازیم

الف) مکمل فازی

(۹-۶)

• برای اینکه تابع C واجد شرایط مکمل باشد باید حداقل دو شرط یااصول زیر را اقناع کند.

اصل موضوع C1 : C(0)=1, C(1)=0 (شرط مرزی)

اصل موضوع C2: برای تمام مقادیر اگر a<b آنگاه (شرط نزولی بودن)

• a,b مقدار تابع عضویت دو عضو هستند.

تعریف: هر تابعی که و اصول موضوع C1 و C2 را ارضاء کند یک عملگر مکمل است.

حال به تعریف چند عملگر مکمل می‌پردازیم [Wang, et al. 1982]:

A. کلاس مکمل فازی سوگنو (sugeno)

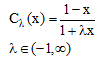
(۱۰-۶)

B. کلاس مکمل یاگر (Yager)

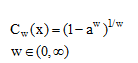(۱۱-۶)

C . کاربردی ترین مکمل معمولاً به فرم زیر است

(۱۲-۶)

ب) اجتماع فازی (s-norms)

(۱۳-۶)

• برای اینکه تابع S واجد شرایط اجتماع باشد باید حداقل چهار شرط یا اصول زیر را اقناع کند.

اصل موضوع s1:

S(0,a)=S(a,0)=a , S(1,1)=1 (شرط مرزی)

اصل موضوع s2:

( S(a,b)=S(b,a (شرط جابجایی)

اصل موضوع s3:

اگر  a≤a’, b≤b’  آنگاه (‘s(a,b) ≤ s(a’,b (شرط صعودی)

اصل موضوع s4:

((S(S(a,b),c)=S(a,S(b,c (شرکت‌پذیری)

تعریف: هر تابع [S:[0,1]×[۰,۱]→[۰,۱ که اصول موضوع S1 تا S4 را ارضاع نماید، یک عملگر اجتماع یا S-norm است.

حال به تعریف چند عملگر S-norm می‌پردازیم [Wang, et al. 1982]:

A. کلاس دومبی (dombi)

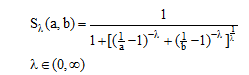
(۱۴-۶)

B. کلاس دبویس- پرید (Dubois-Prade)

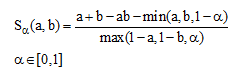
(۱۵-۶)

C. کلاس یاگر (Yager)

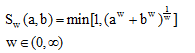
(۱۶-۶)

D. جمع دراستیک (Drastic sum)

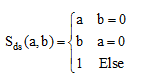
(۱۷-۶)

E. جمع انیشتن

(۱۸-۶)

F. جمع جبری

(۱۹-۶)

G. و کاربردی‌ترین آنها ماکزیمم است.

(a,b)=Max(a,b)

(۲۰-۶)

پ) اشتراک فازی (T-norms)

(۲۱-۶)

• برای اینکه تابع T واجد شرایط اشتراک باشد باید حداقل چهار شرط یا اصول زیر را اقناع کند.

اصل موضوع T1 :

S(1,a)=S(a,1)=a , T(1,1)=1 (شرط مرزی)

اصل موضوع T2:

(T(a,b)=T(b,a (شرط جابجایی)

اصل موضوع T3:

اگر a≤a’, b≤b’ آنگاه (‘T(a,b) ≥ T(a’,b (شرط صعودی)

اصل موضوع T4 :

((T(T(a,b),c)=T(a,T(b,c (شرکت‌پذیری)

تعریف: هر تابع :[۰,۱]×[۰,۱]→[۰,۱] که اصول موضوع T1 تا T4 را ارضاع نماید، یک عملگر اشتراک یا T-norm است.

حال به تعریف چند عملگر T-norm می‌پردازیم [Wang, et al. 1982]:

A. کلاس دومبی (dombi)

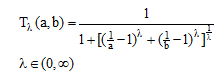
(۲۲-۶)

B. کلاس دبویس- پرید (Dubois-Prade)

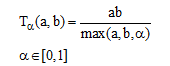
(۲۳-۶)

C. کلاس یاگر (Yager)

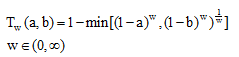
(۲۴-۶)

D. جمع دراستیک (Drastic sum)

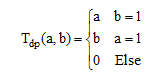
(۲۵-۶)

E. ضرب انیشتن

(۲۶-۶)

F. ضرب جبری

(۲۷-۶)

(T(a,b)=Min(a,b

(۲۸-۶)

• که کاربردی‌ترین آنها مینیمم و ضرب جبری است.

 

۶-۳- اصل توسعه و روابط فازی

۶-۳-۱- اصل توسعه

با معرفی اصل توسعه می‌توانیم عملیات مختلف مجموعه‌های فازی را تعریف کنیم.

اصل توسعه یک معادله اساسی است که اجازه می‌دهد دامنه یک تابع را از نقاطی در مجموعه مرجع U به برد مجموعه‌های فازی در مجموعه مرجع V توسعه دهیم. مشخص¬تر اینکه فرض کنید f:U→V تابعی از مجموعه قطعی U به مجموعه قطعی V باشد. همچنین فرض کنید که یک مجموعه فازی A در U داده شده و ما می‌خواهیم مجموعه فازی B را در V به نحوی معین کنیم که (B=f(a اگر f یک نگاشت یک به یک باشد، آنگاه داریم:

(۲۹-۶)

که f-1(y)، وارون f بوده، بدین معنی است که: f[f^-1(y)]=y. اگر f یک به یک نباشد، آنگاه هنگامی که دو یا چند نقطه متمایز در U با مقادیر تعلق متفاوت در A به یک نقطه یکسان در V نگاشته شوند، ابهامی بوجود خواهد آمد [زاهدی، ۱۳۷۸].

تعریف: نگاشت f:U→V را برای ایجاد رابطه بین مجموعه فازی A بر روی مجموعه مرجع U و مجموعه B بر روی مجموعه مرجع V توسعه می‌دهیم:

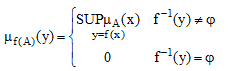
(۳۰-۶)

در حالتی که f یک نگاشت یک به یک است، رابطه قبلی را می‌توانیم به صورت ساده زیر بنویسیم:

(۳۱-۶)

ø علامت مجموعه تهی می‌باشد و  yєV است.

مثال

 

نخست نگاشت زیر را در نظر بگیرید.

Y=3x+2

فرض کنید A مجموعه فازی باشد که حدوداً ۴ را به صورت زیر بدست دهد:

A=0.5/3+1.0/4+0.5/5

همچنین x₁=3 ، x₂=4 و x₃=5 را تعریف می‌کنیم به طوریکه به ازای y_i=3x_i+2; i=1,2,3

چون f یک نگاشت یک به یک است، می‌توانیم (f(A به صورت زیر بکار ببندیم:

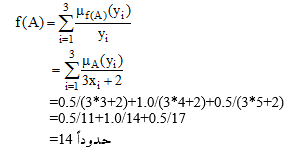
(۳۲-۶)

چون (f(A یک مجموعه فازی متقارن با مقدار عضویت ۱ در ۱۴ است، می‌توانیم این مجموعه فازی را به صورت حدوداً ۱۴ تعبیر کنیم.

 

۶-۳-۲- حاصل ضرب کارتزین فازی

تعریف: فرض کنید x₁,x₂,…,x_n عناصر X₁,X₂,…,X_n باشند. مجموعه همه عناصر (x₁,x₂,…x_n) حاصل ضرب کارتزین X₁,X₂,…,X_n نامیده می‌شود و به صورت X₁×X₂×…×X_n نمایش داده می‌شوند.

تعریف: حاصل ضرب کارتزین مجموعه‌های فازی؛ فرض کنید X₁×X₂×…×X_n حاصل ضرب کارتزین مجموعه‌های مرجع X₁,X₂,…,X_n باشد همچنین فرض کنید A₁,A₂,…A_n مجموعه‌های فازی بر روی X₁,X₂,…,X_n باشند. حاصل ضرب کارتزین مجموعه‌های فازی A₁,A₂,…A_n می‌توان به صورت زیر تعریف کرد [Tanaka, 1998].

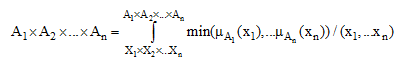
(۳۳-۶)

چون (f(A یک مجموعه فازی متقارن با مقدار عضویت ۱ در ۱۴ است، می‌توانیم این مجموعه فازی را به صورت حدوداً ۱۴ تعبیر کنیم.

 

۶-۳-۳- اصل توسعه بر روی فضای حاصل ضرب کارتزین

تعریف: فرض کنید f نگاشتی از X₁×X₂×…×X_n به Y است که در (y=f(x₁,x₂,…,x_n صدق کند. با توسعه تابع f، f: X1×X₂×…×X_n→Y رابطه بین حاصل ضرب کارتزین A₁×A₂×…×A_n از مجموعه های فازی A₁,A₂,…A_n بر روی x و یک مجموعه فازی مثل ((B=f(A₁×A₂×…×A_n) بر روی Y است که به صورت زیر بدست می‌آوریم [طاهری، ۱۳۷۸]:

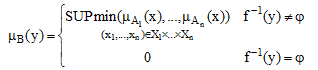
(۳۴-۶)

که در آن f-1(y) به معنی تصویر معکوس y است.

 

۶-۳-۴- رابطه فازی

تعریف: یک رابطه فازی، یک مجموعه فازی است که در فضای حاصل ضرب برداری مجموعه‌های قطعی X₁,X₂,…,X_n تعریف شده است. یک رابطه فازی Q در فضای X₁×X₂×…×X_n مطابق زیر تعریف می‌گردد [Tanaka, 1998]:

{Q={(( x₁, …,x_n),μ_Q(x₁, …,x_n))|( x₁,…,x_n)є X₁× …×X_n

(۳۵-۶)

که [μQ: X1×X2×…×Xn→[۰,۱

مثال

فرض کنید U,V مجموعه اعداد حقیقی باشند. یعنی U=V=R رابطه فازی x تقریباً برابر است با y را می‌توان با تابع تعلق زیر نشان داد:

Μ_AE(x,y)=e^-(x-y)2

مثال

فرض کنید {اصفهان، شهر کرد، زنجان}U= و {شهر کرد،تبریز}V= می‌خواهیم خیلی دور را بین این دو مجموعه از شهرها تعریف کنیم.
در این مثال این رابطه را به صورت فرم ماتریسی نمایش می‌دهیم.

 

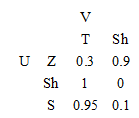
۶-۳-۵- ترکیب روابط فازی

تعریف: ترکیب روابط فازی (Q(V,W), P(U,V) (Composition of fuzzy Relation که با PoQ نمایش داده می‌شود، به صورت یک رابطه فازی در U×W تعریف می‌گردد که تابع عضویت آن مطابق با رابطه زیر محاسبه می‌شود [طاهری، ۱۳۷۸].

(۳۶-۶)

از آنجاییکه T-نرم در رابطه فوق انواع مختلفی داشته باشد، برای هر T-نرم ما ترکیب خاصی خواهیم داشت.

 

۶-۳-۶- اعداد فانتزی

تعریف: یک مجموعه فازی نرمال محدب مانند N از R را یک عدد فازی حقیقی گوییم، اگر:

•  (N(x تک نمایی باشد یعنی دقیقاً یک وجود داشته باشد که N(x0)=1
• (N(x قطعه به قطعه پیوسته باشد.

تعریف: فرض کنید(M є F(R و f:R→R یک عملگر یک بعدی باشد. بر اساس اصل گسترش، عدد فازی (f(M با تابع عضویت زیر تعریف می‌شود.

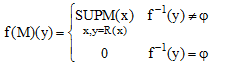
(۳۷-۶)

مثال

اگر f(x)=-x فرض شود، آنگاه قرینه عدد فازی M، عدد فازی –M به صورت زیر است

تعریف: فرض کنید (M, N є F(R با توابع عضویت پیوسته باشند و *:R×R→R یک عمل دوتایی بر اعداد حقیقی باشد اگر تعمیم * را برای اعداد فازی با  نمایش دهیم با استفاده از اصل توسعه حاصل MN به صورت یک مجموعه فازی با تابع عضویت زیر تعریف می‌شود.

(۳۸-۶)

 

۶-۳-۷- اعداد فازی L-R

توابع L,R که شرایط زیر در مورد آنها صادق است را در نظر بگیرید.

•  (L(x)=-L(-x),R(x)=-R(-x
•  R(0)=1, L(0)=1
• توابع L و R نزولیند.

پس یک عدد فازی L-R مثل M به وسیله R-L به صورت زیر تعریف می‌شود.

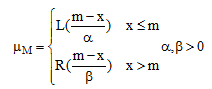
(۳۹-۶)

L و R توابع شکل و m میانگین نامیده می‌شود.

و به اختصار نوشته می‌شود

(۴۰-۶)

تعریف: اعداد فازی اگر دارای خصوصیات زیر باشند اعداد متقارنند

L=R و α=β و با نماد A=(m,α)_L نمایش می‌دهند.

تعریف: اعداد فازی A=(m,α)_Lکه با توابع L بصورتی که در زیر آمده است، به گونه‌های زیر نام‌گذاری می‌شوند.

a. مثلثی

(۴۱-۶)

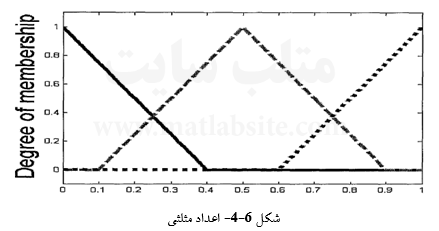
b. نرمال

(۴۲-۶)

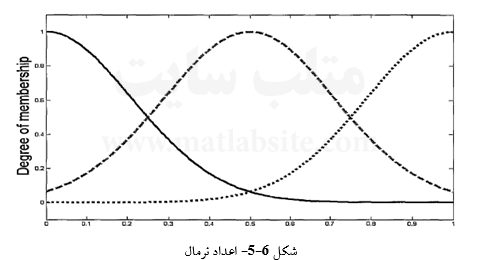
c. سهموی

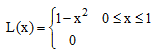
(۴۳-۶)

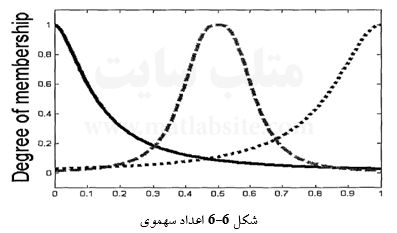
ادامه دارد….

 

آنچه مطالعه کردید، بخش هایی از «فصل ششم» کتاب «بهینه کنترل فعال سازه با رویکرد کلاسیک و هوش مصنوعی» تالیف «جواد پالیزوان (مدرس دانشگاه) و زند علی روشنی (مدرس دانشگاه)»، می باشد که در راستای معرفی و انتشار رایگان جهت استفاده مخاطبین متلب سایت در اختیار این مجموعه قرار داده شده است.

برای تهیه این کتاب می توانید به این لینک(+) مراجعه نمایید.

همچنین آموزش های زیر در فرادرس نیز مباحثی مرتبط با محتوای این کتاب را پوشش می دهند:

• فرادرس آموزش کنترل فعال سازه با رویکرد فازی با میراگر (ATMD)
• فرادرس آموزش طراحی فیدبک حالت بهینه برای سیستم های غیر خطی با الگوریتم های تکاملی
• آموزش طراحی کنترل مقاوم H∞/H2 با استفاده از الگوریتم های تکاملی و فراابتکاری